Развитие пространственных функций – длительный процесс. Он начинается с первых дней жизни ребенка. Сначала ребенок видит предмет и выбрасывает руку по направлению к этому предмету. Позже зрительный контроль определяет не только последнюю точку, но и само дотягивание идет под зрительным контролем, то есть более сложные формы интеграции внутренней и внешней кинестетической информации. Все развитие ребенка в целом оказывает влияние на развитие пространственных функций. Ребенок, который сидит, может лучше ориентироваться в ближайшем пространстве и дотягиваться до разных предметов. У него возникает союз вестибулярного аппарата, кинестетической чувствительности и зрительных функций. Поскольку это комплекс, то важен каждый из компонентов. Если задерживается развитие двигательных функций, ребенок долго не сидит, то и пространственные функции тоже отстают. У слепых детей формирование пространственных функций тоже задерживается.

Существенную роль в развитии пространственных функций играет речь. Ребенок начинает различать и обозначать, сначала различать пассивно за словами взрослого, а потом и активно обозначать различные пространственные отношения. Если в перцептивном плане ребенок сначала осваивает отношения за предметами и находит спрятанные за предметами формы, то в вербальном плане он сначала осваивает предлоги «в», «на», а потом уже другие пространственные конструкции.

Существенно различать конструкции, где смысл предлога ясен из ситуации, так называемые необратимые конструкции, и конструкции обратимые, смысл которых зависит от правильного понимания, какой предмет является точкой отсчета. Например, сравним два предложения: Книга на столе и Книга на журнале. Первая конструкция очень простая (стол не может быть на книге), а другая сложная: нужно понять, что речь идет о книге, а журнал является точкой отсчета. Аналогичный пример – два других предложения: Мальчик ест конфету и Мальчик обидел девочку. В первом предложении слова не могут меняться местами (конфета не может съесть мальчика) – это пример необратимой конструкции. В другом предложении слова могут менять места (как мальчик может обидеть девочку, так и девочка может обидеть мальчика). На этом примере видно, что развитие пространственных функций не ограничивается собственно отношениями в пространстве, но на основании пространственных функций развиваются квазипространственные функции, и для понимания обратимых логико-грамматических конструкций необходимы квазипространственный анализ и синтез, хотя сами конструкции могут быть не связаны с темой пространства.

При разработке методов коррекции зрительно-пространственных функций мы учитывали как последовательность их развития в онтогенезе, так и синдромы нарушения этих функций у взрослых и детей, описанные в нейропсихологической литературе (Лурия, 1969, 2000; Гаджиев, 1966; Цветкова, 1966; Симерницкая, 1985; Ченцов, Симерницкая, Обухова, 1980; Меликян, Ахутина, 2002). Методы восстановления, развития и коррекции пространственных функций широко представлены в литературе (Лурия, Цветкова, 1966; Цветкова, 1972 а, б, 1995, 2001; Семенович, 2002; Манелис, 1997; Семаго, 2000; Семаго, Семаго, 2001; Цыганок и др., 2006; Венгер, Венгер, 1994 и многие другие).

Принципиальный путь развития зрительно-пространственных функций, общий для многих авторов, – это выстраивание занятий в логике хода развития этих функций у детей. Он предполагает последовательно-параллельное включение таких видов работы, как:

¦ ориентация в пространстве тела + вербализация;

¦ ориентация в окружающем пространстве и собственные пространственные перемещения;

¦ пространственные перемещения других предметов;

¦ освоение пространства листа бумаги, овладение геометрическими фигурами, буквами и цифрами;

¦ формирование квазипространственных функций в речи, счетных операциях и решении задач.

Ниже описываются конкретные методы работы, в которых представлено решение некоторых из перечисленных выше задач на привлекательном для детей игровом материале разного уровня сложности. Это методические комплексы заданий на конструирование, компьютерные игры и бланковые методики для освоения пространства листа, рабочей строки и клетки, овладения геометрическими фигурами и цифрами.

1. Венгер Л. А., Венгер А. Л. Готов ли ваш ребенок к школе? —М., 1994.

2. Гаджиев С. Г. Нарушение наглядной интеллектуальной деятельности при поражениях лобных долей мозга // Лобные доли и регуляция психических процессов / Под ред. А. Р. Лурия и Е. Д. Хомской. – М., 1966. – С. 618–640.

3. Лурия А. Р. Высшие корковые функции человека. – М., 1969;2000.

4. Лурия А. Р. Цветкова Л. С. Нейропсихологический анализ решения задач. – М., 1966.

5. Манелис Н. Г. Развитие оптико-пространственных функций в онтогенезе // Школа здоровья, 1997. – Т. 4. – № 3. —С. 25–37.

6. Меликян З. А., Ахутина Т. В. Состояние зрительно-пространственных функций у детей в норме и с задержкой психического развития // Школа здоровья, 2002. – № 1. —С. 28–36.

7. Семаго Н. Я. Современные подходы к формированию пространственных представлений у детей как основы компенсации трудностей освоения программы начальной школы // Дефектология, 2000. – № 1.

8. Семаго Н. Я., Семаго М. М. Проблемные дети. Основы диагностической и коррекционной работы психолога. – М., 2001.

9. Семенович А. В. Нейропсихологическая диагностика и коррекция в детском возрасте. – М., 2002.

10. Ченцов Н. Ю., Симерницкая Э. Г., Обухова Л. Ф. Нейропсихологический анализ нарушений пространственных представлений у детей и взрослых //Вестник Московского университета. Серия 14. Психология, 1980. – № 3.

11. Симерницкая Э. Г. Мозг человека и психические процессы в онтогенезе. – М., 1985.

12. Цветкова Л. С. Нарушение конструктивной деятельности при поражениях лобных и теменно-затылочных отделов мозга // Лобные доли и регуляция психических процессов / Под ред. А. Р. Лурия и Е. Д. Хомской. – М., 1966. – С. 641–663.

13. Цветкова Л. С. Восстановительное обучение при локальных поражениях мозга. – М., 1972.

14. Цветкова Л. С. Нарушение и восстановление счета при локальных поражениях мозга. – М., 1972.

15. Цветкова Л. С. Мозг и интеллект. – М., 1995.

16. Цветкова Л. С. и др. Актуальные проблемы нейропсихологии детского возраста. – М., 2001.

17. Цыганок А. А., Виноградова А. Л., Константинова И. С. Развитие базовых познавательных функций с помощью адаптивно-игровых занятий. – М., 2006.

Развитие зрительно-пространственных функций – важная предпосылка возможности обучения ребенка в школе. Придя в школу, ребенок сталкивается с широким кругом пространственных задач, включая ориентировку в помещении школы и класса, в схеме тела, в пространстве листа, рабочей строки и клетки, в структуре буквы и цифры. Определенный уровень созревания пространственных функций нужен и для развития квазипространственных операций, лежащих в основе понимания обратимых логико-грамматических конструкций, освоения счета, решения арифметических задач и др. (Лурия, 1969). Становление пространственных функций – длительный и весьма уязвимый процесс (Ахутина, Золотарева, 1995; Манелис, 1997; Семенович, Умрихин, 1998). В связи с этим понятна важность ранней диагностики и своевременной коррекции пространственных функций.

Традиционно для исследования зрительно-пространственных функций используются методики, основанные на копировании, повороте на 180° или запоминании (с узнаванием или воспроизведением) пространственно ориентированных фигур. Это, например, задания на конструктивный праксис (копирование фигур с их перевертыванием), тест Рея – Тейлора, тест на зрительно-моторные координации (VMI test). Наряду с ними широко применяются методики, предполагающие складывание фигур по заданному образцу из палочек, кубиков Кооса, из карточек (плоскостной вариант кубиков Кооса). Хорошо известны пробы на складывание фигуры из деталей, так называемые задания на перцептивное моделирование, где ключевым моментом выступает зрительно-пространственная ориентировка. Варианты этих методик используются в коррекционно-развивающих целях. Так, к методике Кооса восходит один набор заданий из известной книги Б. П. Никитина «Развивающие игры».

Описываемая здесь работа с методиками «Сложи фигуру» и «Черные и белые квадраты» проводилась в 1-м классе школы Комплекса социальной помощи детям и подросткам МКО. Учащиеся класса нуждались в коррекционной работе в связи с неравномерностью и отставанием в развитии высших психических функций. Решение пространственных задач было дефектным у всех детей, но у одних оно было связано с недоразвитием собственно пространственных функций, а у других – со слабостью программирования и контроля и/или нейродинамическими особенностями деятельности (повышенная истощаемость, флуктуации внимания).

Методика «Черные и белые квадраты» финского психолога Мерьи Саарела (Saarela, 1995) предполагает складывание определенных фигур из черных квадратных панелей. Ребенок выполняет узор, вкладывая панели в рамку с девятью белыми клетками (3 х 3 см). Значительный размер панелей (11 х 11 см) и наличие ручки облегчают использование методики детьми с моторными трудностями (рис. 4.2.1).

Предложенные автором образцы фигур упорядочены от простого к сложному. Они представлены в двух размерах: во-первых, в натуральную величину (это позволяет использовать их как основу для накладывания панелей), а во-вторых, в уменьшенном размере. Вариация содержания и размера образцов создает широкий диапазон сложности заданий, вследствие чего методика может служить как для диагностического прослеживания состояния зрительно-пространственных функций, так и для их коррекции у разных категорий детей.

Наш опыт применения методики «Черные и белые квадраты» подтвердил это. Кроме того, было обнаружено, что благодаря хорошему дизайну дети охотно работают с методикой. Положительное влияние повышенной мотивации на работоспособность детей

Рис 4.2.1. Образцы и оборудование методики «Черные и белые квадраты» М. Саарела

и возможность сосредоточить внимание позволяют более четко увидеть первичные проблемы детей – собственно пространственные трудности или сохраняющиеся трудности программирования и контроля. Рассмотрим диагностические возможности методики, раскрывая на примерах качественные особенности выполнения проб детьми с различными первичными трудностями.

С этой целью проанализируем выполнение заданий двумя ученицами 1-го класса. У Ани Г. оно было затруднено из-за недоразвития программирования и контроля и вторичных пространственных трудностей. Анализ выполнения проб этой девочкой обнаружил следующее:

¦ трудности вхождения в задание (проба 1 выполнена за 20 с, последующие четыре не превышали 3 с на каждую);

¦ манипуляции по типу проб и ошибок (проявившиеся наиболее отчетливо в пробах 8 и 15, выполненных за 20 и 95 с соответственно);

¦ трудности нахождения нового принципа решения задачи (как в пробе 16, где девочке необходимо было подсказать, что центральная фигура составляется из 4 панелей, или как в пробе 19, где было отчетливое увеличение времени ответа – до 124 с).

За всеми этими особенностями выполнения задания стоят недостаточность ориентировочно-исследовательской деятельности и трудности выработки плана, нахождения способа решения задачи.

Иной характер носили трудности выполнения задания у Насти И., у которой отмечалось отставание в развитии собственно пространственных функций, входящее в синдром недоразвития функций правого полушария.

Остановимся несколько подробнее на анамнезе и нейропсихологической картине недоразвития высших психических функций у этой девочки.

Настя И., 8 лет, повторяет программу 1-го класса. Год назад при поступлении в Комплекс социальной помощи детям и подросткам ей был поставлен диагноз: выраженная задержка психического развития, возможно, умственная отсталость, элективный мутизм.

В анамнезе: родилась через кесарево сечение, недоношенной (7 мес.), вес при рождении – 2600 г, в 4 мес. – закрытая черепно-мозговая травма. Контакт с матерью недостаточный. Развитие речи шло с отставанием: слова – в 4 года, фразовая речь – в 5,5 года. При поступлении в Комплекс в речевой контакт вступала очень редко и только с дедушкой и бабушкой и еще реже – со сверстниками (элективный мутизм).

Нейропсихологическое обследование при поступлении было затруднено из-за нежелания девочки вступать в речевой контакт и негативных реакций на многие задания. В начале повторного учебного года девочка постепенно стала отвечать воспитателю и учителю во время игры и внеклассных занятий, а потом и на уроке.

Нейропсихологическое обследование девочки, проведенное в ходе коррекционных занятий, обнаружило отчетливо диссоциативное развитие зрительных и зрительно-пространственных функций (первые нормативны, вторые – грубо дефектны) на фоне отставания в развитии других высших психических функций по типу правополушарной недостаточности.

При диагностическом обследовании методикой «Черные и белые квадраты» было выявлено следующее.

Нулевую пробу (черный кубик в левом нижнем углу) выполняла зеркально, ставя черную панель в верхний угол. Из семи первых проб девочке было доступно выполнение 3-й, 4-й и 6-й, характеризующихся наибольшей простотой. Но уже и здесь отмечалась особая стратегия выполнения задачи: в пробе 4 девочка строила фигуру, начиная с правой стороны и снизу вверх. В пробе 1 отчетливо выявилась фрагментарность восприятия: целостную фигуру девочка разрывала на две части. В пробах 2 и 5, узор которых похож на русские буквы «П» и «Н», Настя И. не опознала букв, несмотря ни на наводящие вопросы, ни на то, что буква «Н» – первая буква ее имени. В пробе 2 девочка не могла выявить пространственную структуру и дважды выстраивала далекие от образца фигуры, давала зеркальное изображение фигуры, путая верх-низ, а затем поворачивая фигуру на 90°. Аналогичные ошибки (утеря фигуры, зеркальное воспроизведение, а также трудности переключения с предыдущей структуры на новую) отмечались при построении фигур 5 и 7 (рис. 4.2.2).

В связи с недостаточной успешностью мотивация девочки к выполнению задания снизилась, и потому дальнейшие пробы ей не предлагались. Однако результаты уже сделанных восьми проб отчетливо показали весь диапазон пространственных трудностей девочки: фрагментарность восприятия, трудности схватывания зрительного гештальта, ошибки в ориентировании фигуры поворот на 90°, мена верх-низ, справа-слева), тенденция к левоcтороннему игнорированию (последовательность работы – с правой стороны снизу вверх).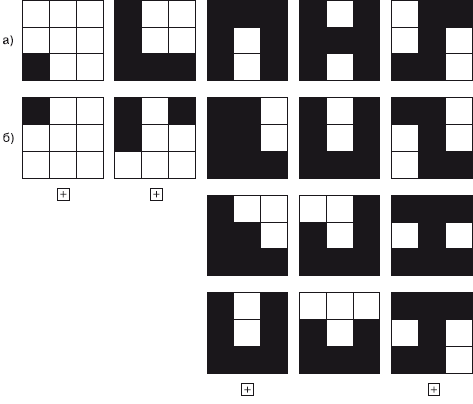

Рис. 4.2.2. Выполнение заданий Настей И.: а – образцы; б – выкладывание на панели; + – правильное выполнение

Перейдем к использованию методик «Сложи фигуру» в корекционных целях. Для этого рассмотрим варианты заданий, редлагавшихся Насте И.

Девочка, наряду со школьными уроками, посещала индивиуальные и групповые (группа от 2 до 6 человек) занятия с нейропсихологом. Программа работы с учителем (Э. В. Золотарева) нейропсихологом (Н. М. Пылаева) включала комплекс методик, направленных на коррекцию и развитие зрительно-пространственных функций. В него входили задания на отработку схемы тела, на ориентировку в классе, игровой комнате, в пространстве стола и листа, а также блок заданий на перцептивное моделирование «Сложи фигуру».

Указанный блок заданий был направлен на составление целого изображения из частей: это могли быть изображения предметов, сюжетов, геометрических фигур, ранжированных по перцептивной сложности. Существенно отметить, что сходные задания применяются и для развития зрительно-вербальных функций (Пылаева, Ахутина, 1995; см. также главу 6 части 2). Методики различаются прежде всего выбором материала: для развития зрительно-пространственных функций материалом служат изображения тех объектов, для восприятия которых ключевыми выступают пространственные характеристики.

Первый, самый простой, вариант предполагал складывание из деталей, а затем и карточек (по типу плоскостного варианта методики Кооса) изображений реальных объектов: дома, елки, бабочки, цветка (рис. 4.2.3). Сначала отрабатывалось складывание фигуры по образцу; если оно было успешным, за ним следовало складывание по памяти; затем рисование фигуры. Если предъявление образца не приводило к успеху, то ребенку предлагалось обвести образец (тем самым приготовить шаблон), затем сложить фигуру по шаблону.

После отработки складывания по шаблону и без него следовали выполнение задания по памяти и рисование. Изготовление шаблона практиковалось также и в случае успешного складывания для закрепления конструктивной деятельности в графических заданиях: он служил опорой для рисования фигуры.

Графические задания требовали вычленения ключевых точек, нахождения их местоположения в соответствующих по размеру рамках и на листочке, разграфленном в клеточку, как в школьной тетради.

Второй набор заданий предполагал переход от складывания отдельных реальных объектов к изображению сюжета. Это реализовывалось с помощью пластмассовых кубиков, укрепляемых

Рис. 4.2.3. Образцы заданий «Сложи фигуру»

на панели со штырьками (кубики наряду со сплошной закраской имели и прямую, и закругленную линию разделения цветов, как в плоскостном варианте методики Кооса). Дети изображали домик, забор, елку, грибок, солнце. Складывание фигур и геометрических деталей по типу «плоскостного Кооса» представляет более сложную перцептивную деятельность по сравнению со складыванием фигур из конкретных частей (часть крыши, часть елки и т. п.). Оно требует более детального анализа образца и предварительного ориентирования элементов.

Третий набор заданий – адаптированная нами методика «Черные и белые квадраты». С одной стороны, она была сложнее предшествующих, поскольку рамка содержит 9 ячеек, в отличие от предыдущих, где, как правило, 4. С другой стороны, она несколько проще, поскольку составляющие фигуру элементы – целостные одноцветные квадраты (без деления на два цвета, как в ранее используемых кубиках). Переход к перцептивно более сложным фигурам удачно сочетается с более простым видом деятельности – вкладыванием в рамку крупных деталей с удобной ручкой. Это разнообразит дидактический материал, позволяя перейти от пластмассовых деталей, карточек, кубиков на панели к новым объектам.

При применении методики «Черные и белые квадраты» в коррекционных целях, как и в предыдущих заданиях, использовался широкий набор выполняемых действий:

¦ анализ рамки и образца;

¦ построение фигур по образцу и по памяти;

¦ поиск соответствующего выстроенной фигуре образца;

¦ выстраивание фигуры по образцу меньшего размера;

¦ графическое воспроизведение рамки и образца меньшего размера на листе в клеточку; при затруднениях – анализ построения рамки, вычленение и перенесение опорных точек;

¦ обведение контура фигуры, выполняемого самостоятельно или по намеченному педагогом пунктиру, раскрашивание фигуры;

¦ складывание фигуры из элементов меньшего размера (1 х 1 см).

Кроме варьирования размеров образца, может меняться и его положение: в горизонтальной или вертикальной плоскости.

Рассмотрим, как протекала работа по этой методике с Настей И.

Вначале шло знакомство с рамкой, девочка снимала все панели, пересчитывала количество клеток, определяла количество клеток с каждой стороны, находила центральную клетку, ряд сверху, ряд снизу, затем ряд слева, ряд справа. По аналогии с действиями на уроках в классе она находила левую верхнюю клетку, правую верхнюю клетку и т. д.

Затем предлагался нулевой образец. Девочка отвечала на вопросы: «Черный квадрат сверху или снизу? Справа или слева?». После вербального анализа образца девочка находила соответствующее место в рамке и накладывала панель. Далее педагог предъявлял на листе бумаги рамку меньшего размера и просил найти ту же позицию в ней. Соответствующая клеточка обводилась и раскрашивалась. Аналогично выполнялись фигуры 1, 2 и 3 (рис. 4.2.4).

Затем девочку попросили самостоятельно построить эти фигуры в большой рамке, и она успешно построила их и фигуру 4.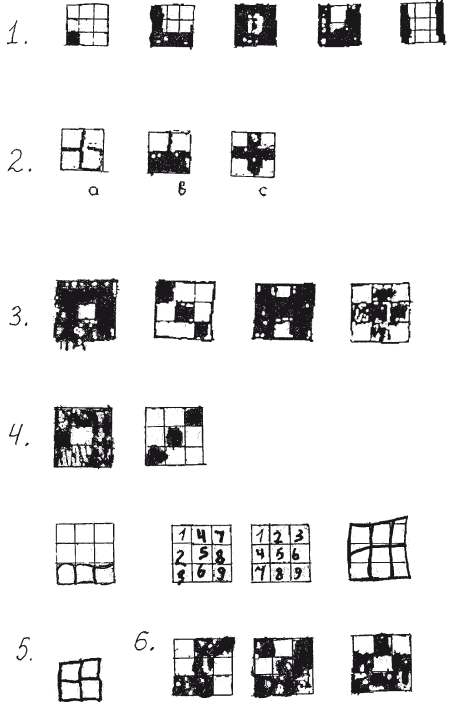

Рис. 4.2.4. Копирование фигур Настей И.

В следующем задании на копирование, в целом правильно воспроизведя образец, Настя заштриховывала неточно, игнорируя структуру рамки (см. рис. 4.2.4).

Более грубые ошибки выявились при выполнении пробы 14. Хотя девочка правильно сложила фигуру, при переходе к графическому выполнению задания она сначала рисовала крест фрагментарно, затем при попытке заштриховать теряла структуру (см. рис. 4.2.4, фигура 2 а, b). Чтобы добиться правильного выполнения, педагог вновь возвращался к развернутому совместному анализу образца и после обсуждения отмечал пунктиром контуры фигуры, которую девочка заштриховывала (см. рис. 4.2.4, фигура 2 с).

На следующем этапе сохранялось предварительное выстраивание фигур, а структура графической части задания менялась за счет повышения самостоятельности ученицы.

Для работы выбирались легко семантизируемые фигуры: буквы «О» и «Н», «лестница», знак «плюс». Фигуры 1 и 3 (буквы «О» и «Н») предполагали вычленение пустых клеток, две другие – заштрихованных.

Девочка легко выстроила фигуры из панелей, без труда нашла соответствующие маленькие образцы. Для копирования фигуры педагог предлагал нарисованную рамку, и после совместного обсуждения девочка сама выделяла контуры фигур, а затем заштриховывала. Здесь уже не встречались грубые ошибки по типу утраты фигуры при заштриховке, ярко выделенные границы штриховки учитывались девочкой, хотя она их иногда пересекала из-за плохой моторики.

Позднее выполнение проделанных проб закреплялось, структура графического действия сокращалась: после обсуждения с педагогом девочка самостоятельно заштриховывала фигуры без предварительного рисования контуров (см. рис. 4.2.4, фигура 4).

Важным этапом коррекционной работы стало обучение ребенка самостоятельному рисованию рамки. В начале работы с методикой «Сложи фигуру» проводился анализ рамки, что позволило применять готовую рамку при накладывании панелей, а затем и в графических действиях. На новом этапе девочка шла от пассивного использования рамки к ее самостоятельному конструированию.

Когда девочке дано было задание нарисовать рамку, она начала рисовать ее поэлементно, обводя клеточку за клеточкой (см. рис. 4.2.4, фигура 5). Чтобы уйти от фрагментарности и дать возможность девочке рисовать целостную структуру рамки, педагог «материализовал» структуру рамки, нумеруя клетки вместе с девочкой. После обсуждения педагог писал в верхней клеточке цифру 1, девочка находила следующую клетку, используя стратегию «сверху вниз», педагог подхватывал эту стратегию, а потом предлагал другую (см. рис. 4.2.4, фигура 5).

После такой проработки девочка сделала попытку нарисовать целостную структуру рамки: она правильно обвела квадрат со сторонами в три клетки, затем правильно расчленила квадрат линиями сверху вниз, но в горизонтальном членении она ошиблась. Следующая попытка оказалась успешной, и в приготовленной рамке девочка правильно нарисовала сложную фигуру (см. рис. 4.2.4, фигура 6).

Таким образом, в графическом плане было отработано выполнение заданий, не требующих смещения частей относительно ячеек рамки.

Контрольное исследование построения фигур 1-14 показало значительно более высокую успешность девочки. Она правильно выполнила задания 2–6, 8, 11 и 14, затратив на все фигуры, кроме 8-й, от 3 до 16 с (10, 3, 5, 7, 15, 11, 16); лишь фигура 8 (белый крест) потребовала развернутой ориентировки, время ее выполнения – 59 с (черный крест был сделан за 16 с).

С остальными шестью заданиями девочка тоже справилась, но по ходу выполнения допустила ошибки: две – по типу зеркальности; одну – мена фигуры и фона; три – из-за недостаточного анализа образца. Ошибки по типу зеркальности девочка исправляла самостоятельно, остальные – при привлечении ее внимания к образцу.

В целом, комплекс методик, направленных на развитие зрительно-пространственных функций, позволил Насте И. значительно продвинуться в освоении школьных навыков, в овладении письмом, чтением и счетом. Это наглядно видно при сравнении ее письменных работ в начале и в конце учебного года. Если учесть, что девочка вплоть до середины октября регулярно писала свое имя с ошибками, пропуская гласную и переставляя гласные, то результаты контрольного диктанта впечатляют: из первых 20 слов она 17 пишет правильно, а далее на фоне утомления в последних четырех словах делает специфические ошибки, главным образом пропуск гласных (подробнее о типичных ошибках см.: Ахутина, Золотарева, 1997, а также главу 6 данной части). Эти ошибки, как и несоблюдение размера и наклона букв, показывают, что первичный дефект (задержка формирования зрительно-пространственных функций) у девочки сохраняется, хотя он и претерпел значительное обратное развитие, что позволило овладеть базовыми школьными навыками.

Итак, апробация системы методик «Сложи фигуру» для коррекции зрительно-пространственных функций обнаружила ее эффективность. Методики позволяют менять формы работы (конструктивные и графические) и степень сложности заданий, и потому с их помощью можно отрабатывать зрительно-пространственный гнозис и праксис, переходя от совместных развернутых действий к самостоятельным свернутым действиям ребенка.

1. Ахутина Т. В., Золотарева Э. В. О зрительно-пространственной дисграфии: нейропсихологический анализ и методы коррекции // Школа здоровья, 1997. – Т. 4. – № 3. – С. 37–42.

2. Лурия А. Р. Высшие корковые функции. – М., 1969.

3. Манелис Н. Г. Развитие оптико-пространственных функций в онтогенезе // Школа здоровья, 1997. – Т. 4. – № 3. – С. 25–37.

4. Пылаева Н. М., Ахутина Т. В. Коррекция зрительно-вербальных функций у детей 5–7 лет // Школа здоровья, 1999. – № 2. – С. 65–71.

5. Семенович А. В., Умрихин С. О. Пространственные представления при отклоняющемся развитии (методические рекомендации к нейропсихологической диагностике). – М., 1998.

Целью представленного цикла является развитие зрительно-пространственных функций детей 5–8 лет в ходе выполнения игровых заданий.

В этих заданиях ребенок практически овладевает навыками и умениями ориентировки в пространстве, учится выражать пространственные отношения как в наглядных схемах, так и в понятиях.

Цикл рассчитан на 18–20 получасовых занятий, которые целесообразно проводить не реже 2–3 раз в неделю. Соответственно, длительность курса может варьироваться от 1,5 до 3 месяцев. Занятия проводятся индивидуально или в микрогруппах из 2–4 человек.

Развивающий эффект проводимых занятий отслеживается в ходе выполнения заданий (сокращение необходимой помощи взрослого и времени выполнения задания, уменьшения числа и степени грубости ошибок). Эффективность занятий контролируется методикой Кооса, которая проводится до и после развивающего цикла.

Для заданий необходимы карточки по типу «плоскостного Кооса», то есть разноцветные квадраты, одни из которых закрашены полностью одним цветом, а другие, разделенные по диагонали, – двумя цветами. Во всех заданиях этого типа ведущий выкладывает из карточек образец, а дети после анализа карточек и образца копируют его.

На рисунках ниже все изображения черно-белые, однако по аналогии со сторонами кубиков Кооса карточки могут быть также красно-белыми и желто-синими. Если первый раз ведущий сложил домик черно-белый, в следующий раз он может изменить цвета карточек, чтобы ребенок воспринимал это задание как новое.

Задание 1. «Найди по образцу».

Ребенок подкладывает карточки в соответствии с образцом (рис. 4.3.1).

Рис. 4.3.1. К заданиям 1 и 2

Задание 2. «Рассмотри и расскажи».

«Какая часть закрашена на третьей фигуре? (Левая верхняя.) А на четвертой?» и т. д. (см. рис. 4.3.1).

Задание 3. «Домик».

Перед ребенком набор карточек 1–6 и рисунок домика.

«Посмотри на домик и покажи, какие карточки тебе дать, чтобы построить такой домик. Построй домик».

Задание 4. «Домик и елочка». Выбери карточки для домика и построй его. Выбери карточки для елочки и сложи ее (рис. 4.3.2).

Рис. 4.3.2. К заданиям 3 и 4 Задание 5. Поворот карточки.

Выкладываются четыре карточки, разделенные по диагонали (рис. 4.3.3).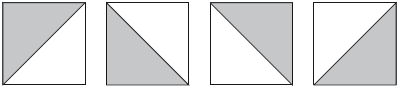

Рис. 4.3.3. К заданиям 5-7

Ребенку дают еще одну такую же и спрашивают:

«Она может быть похожа на первую карточку? Положи карточку так, чтобы они были одинаковыми. Теперь положи карточку под вторую, чтобы они тоже были одинаковыми. Что ты сделал с карточкой?» (Повернул.)

Таким же образом отрабатываются карточки 3 и 4. Тем самым ребенок подводится к выводу, что при вращении одной карточки получается любой из четырех вариантов.

«Давай нарисуем 4 карточки. Вот квадрат. Мы соединяем противоположные уголки и одну половину закрашиваем». (Психолог выделяет два угла, которые ребенок соединяет.)

Задание 6. «Отгадай карточку».

Перед ребенком 4 карточки (см. рис. 4.3.3).

«Сейчас я загадаю одну карточку, а ты найди ее. У нее левый верхний угол красный. А теперь найди другую карточку – у нее левый нижний угол красный. Найди карточку, где правый нижний угол красный».

Задание 7. «Загадай карточку».

Перед ребенком и психологом, сидящим рядом, лежат те же 4 образца (см. рис. 4.3.3).

«Загадай мне карточку, а я найду ее». (По аналогии с предыдущим заданием отрабатывается речевое описание положения карточки.)

Задание 8. «Делаем цветок».

«Построй такой цветок. Расскажи, где будут красные углы». (На первой карточке – в левом нижнем углу, на второй… и т. д.) (рис. 4.3.4).

Задания 9-12. «Сложи фигуру».

Дети строят бабочку, песочные часы, бантик и окошко. При затруднениях ребенку предлагается сказать, где находится цветной угол на образце (рис. 4.3.5).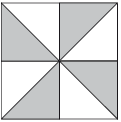

Рис. 4.3.4. К заданию 8

Рис. 4.3.5. К заданиям 9-13

Количество заданий, их повторение регулируются психологом в зависимости от утомляемости ребенка и степени усвоения материала. Хорошему усвоению способствуют задания «Придумай свою фигуру» и соревнования на скорость.

Задание 13. «Нарисуй фигуру».

«Вспомни, пожалуйста, какие фигуры ты сегодня складывал». (Ребенок перечисляет.) «Нарисуй, какие фигуры тебе понравились». (Ребенку дается лист бумаги с 4 рамками-квадратами, разделенными по вертикали и горизонтали на 4 части.) При затруднении вспомнить или нарисовать фигуру используется опора на образец (см. рис. 4.3.5).

Задание 14. «Сложи ромб».

Перед ребенком лежат карточки, направленные вниз углом, а не, как обычно, стороной, и образец фигуры (рис. 4.3.6).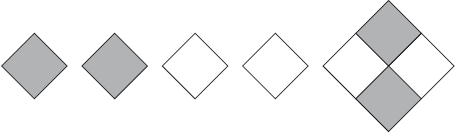

Рис. 4.3.119. К заданию 14

«Ты уже хорошо научился складывать разные фигуры. Попробуй сложить такую. Ты обратил внимание, как лежат карточки?»

Задания 15–16. «Сложи бантик и лодочку». При необходимости психолог выделяет границы одной или каждой из четырех карточек (рис. 4.3.7).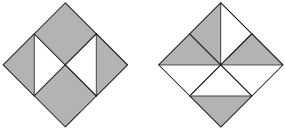

Рис. 4.3.7. К заданиям 15 и 16

Во всех заданиях этого раздела ребенку дают образец и карточки по типу «плоскостного Кооса».

Задание 1. «Конфета-карамель».

«Ты узнал, на что похожа эта фигура? Да, действительно, она похожа на конфету. Сколько карточек тебе нужно для этой фигуры? Сколько одноцветных карточек? Сколько двухцветных карточек? Выбери цвет и сложи конфету» (рис. 4.3.8).

Рис. 4.3.8. К заданию 1

Задание 2. «Шоколадная конфета».

«Первая конфета была карамелька, а теперь давай сложим шоколадную конфету. Сколько и каких карточек тебе нужно? Выбери и сложи» (рис. 4.3.9).

Рис. 4.3.9. К заданию 2

Задания 3–4. «Лодочка и рыбка».

Эти фигуры строятся аналогично (рис. 4.3.10).

Рис. 4.3.10. К заданиям 3-5

Задание 5. Срисовывание фигуры по образцу.

«Какая фигурка тебе понравилась больше? Давай ее срисуем». (Дается незаполненная рамка из 8 или 10 частей.)

Для выполнения заданий требуется конструктор «Лего» «Дакта» или его аналоги.

Задание 1. Сортировка фигур набора «Дакта» по форме.

Образцы фигур представлены на рис. 4.3.11.

Рис. 4.3.11. К заданиям 1 и 2

Задание 2. Игра «Запомни».

«Какая форма тебе больше всего нравится?» (Ребенок показывает и называет.) «Отбери все такие же фигуры».

Педагог или другой ребенок отбирает все фигурки любой другой формы. Детальки переворачиваются, и проводится игра по типу «Memory» – каждый играющий может открыть две детальки. Если обе они оказываются одинаковыми, он забирает их себе и сохраняет ход. Если фигуры разные, детальки возвращаются – и ход переходит к другому игроку. Выигрывает тот, кто соберет больше пар фигур.

Возможен другой вариант игры, когда каждый играющий выбирает «любимую» фигуру, тогда подсчитывается, сколько пар «любимых» фигур собрал каждый.

Задание 3. «Найди недостающую деталь».

Ребенку предъявляется карточка из набора «Лего» «Дакта», и ему предлагают закончить «елочку», узоры и «лодочку», то есть найти к каждой фигуре одну деталь (рис. 4.3.12).

Рис. 4.3.12. К заданию 3

«А теперь давай сложим один узор. Поставь фигурку, у которой левый нижний угол красный. Под ней поставь фигурку, у которой левый верхний угол красный. Ты догадался, какой узор мы складываем? Закончи ее. Какую половину ты достраиваешь – левую или правую?»

Задание 4. «Построим домик».

Ребенку показывают карточку (рис. 4.3.13).

Рис. 4.3.13. К заданию 4

«Это домик. В нем три этажа и три подъезда. Домик будет веселей, если на каждом из этажей будут жить фигурки одного цвета, например на первом этаже – зеленого. Построй первый этаж. А какого цвета фигуры будут жить на втором этаже? А на третьем? У тебя получился хороший дом. Какие фигуры над зелеными? Какие фигуры справа от среднего подъезда? А какие слева?»

Задание 5. «Змейка».

«Давай сделаем змею. Какая у змеи будет голова? Поставь детальку в левый верхний угол панели. А теперь будем делать туловище и хвост. Поставь следующую деталь – она должна отличаться от предыдущей или цветом, или формой. Например, после красного треугольника может идти любая красная фигура, но не такой же треугольник. А если ты выберешь такую же форму, то она должна быть другого цвета. Двое играющих ставят детали по очереди, ошибающийся теряет ход».

Задание 6. «Паровоз».

Ребенку предлагают образец и детали из набора «Лего» «Дакта» (рис. 4.3.14).

Рис. 4.3.14. К заданию 6

«Сложи паровоз. Начни с трубы. Ставь следующую деталь и говори, куда ставишь (под, над, справа)».

Затем ребенку дают лист в крупную клетку и предлагают перерисовать паровоз.

Задание 7. Складывание по образцу меньшего размера.

Ребенку даются картинка-образец и необходимые для ее складывания детали (рис. 4.3.15).

Рис. 4.3.15. К заданию 7

«Давай подумаем, что здесь нарисовано? (Елка, солнце, забор и ворота.) Давай построим ворота. Какие кубики нужны для нижней части? Верхней? Поставь их на панель».

Аналогично строятся и другие детали картинки, таким образом у ребенка вырабатывается стратегия упорядоченного считывания элементов образца.

Ребенку предъявляется рамка с девятью белыми клетками и девятью черными панелями с ручками. Ребенок выполняет узор, вкладывая (или снимая) эти панели в рамку. Размер панелей (11 х 11 см) и наличие ручки облегчают использование методики детьми с моторными трудностями (методика первоначально разработана финским психологом М. Саарела, подробнее см.: Пылаева, Ахутина, 2000 или предыдущую главу).

Задание 1. Знакомство с материалом.

«Сними все панели, пересчитай, сколько здесь клеток. Найди центральную клетку, ряд сверху, ряд снизу, затем ряд слева, ряд справа. Скажи, сколько клеток в каждом ряду. Найди левую верхнюю клетку, правую верхнюю клетку и т. д. Поставь черный квадрат в середину. А теперь – в левый верхний угол» (рис. 4.3.16).

Рис. 4.3.16. К заданию 1

Задание 2. Построй фигуру.

Ребенку последовательно предъявляют на карточках образцы меньшего размера, чем рамка, и предлагают сложить фигуру

(рис. 4.3.17).

Рис. 4.3.17. К заданиям 2 и 3

Задание 3. Построение по памяти.

«Вспомни, какие ты строил фигуры, и построй их еще раз».

Задание 4. «Сложи буквы».

Ребенку дают образец и спрашивают, узнал ли он букву. Затем предлагают сложить ее.

Далее ребенку последовательно предъявляют образцы, и он складывает буквы (рис. 4.3.18).

Рис. 4.3.18. К заданиям 4-6

Задание 5. Построение букв по памяти.

«Вспомни, какие ты строил буквы, и построй их еще раз в том же порядке. Какую первую букву ты строил? А вторую?» и т. д.

Задание 6. Рисование по памяти.

Ребенку дают лист бумаги в клетку.

«Давай нарисуем эти буквы. Сначала нарисуй рамку». (При затруднениях психолог намечает опорные точки рамки, ребенок рисует ее и делит с помощью психолога на части.) «А теперь нарисуй эту букву. Выбери карандаш твоего любимого цвета. Какие клетки ты закрасишь? А теперь следующую нарисуй другим цветом, но сначала приготовь рамку».

Задание 7. Построение знакомых фигур.

Ребенку последовательно предъявляют образцы и спрашивают, на что они похожи (лесенка, черный и белый кресты, шахматная доска) (рис. 4.3.19).

Рис. 4.3.119. К заданию 7

«Сделай лесенку. Скажи, куда ты положил черные квадраты». (В левую нижнюю клетку и т. д.)

Аналогично с проговариванием строятся другие образцы.

Задание 8. «Диктант фигур».

Ребенку дается карточка, и он командует психологу, как построить фигуру («Поставьте черный квадрат в нижний левый угол».) (рис. 4.3.20).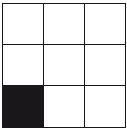

Рис. 4.3.20. К заданию 8

Для этого задания могут быть использованы и другие образцы. Психолог может «ошибаться» в выполнении задания.

Задание 9. Идентификация и запоминание фигур.

Перед ребенком выкладывают три карточки с образцами фигур (рис. 4.3.21).

Рис. 4.3.21. К заданию 9

Психолог на панели кладет среднюю фигуру.

«Покажи, какую фигуру я сложила. Посмотри на нее внимательно – сейчас ты ее будешь строить сам».

После этого психолог предъявляет и просит воспроизвести по памяти сначала первую фигуру, а потом третью. Одна фигура может быть сложена, а другая нарисована.

Задание 10. «Развиваем глазомер».

Перед ребенком две карточки-образца (рис. 4.3.22).

«Какие здесь буквы?» («Т» заглавная и «т» маленькая.) «Построй большую букву. Ты это делал и справился легко. Теперь попробуй маленькую». При затруднениях дается подсказка: «Посмотри, где граница клеток».

Рис. 4.3.22. К заданию 10

Задание 11. Построение фигур со смещением.

Ребенку последовательно предъявляют образцы и спрашивают, на что они похожи (пирамида, колодец, мишень и мельница) (рис. 4.3.23).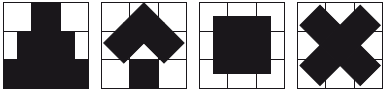

Рис. 4.3.23. К заданию 11

Ребенок строит фигуры с опорой на образец и повторяет по памяти.

Возможна отработка заданий в графическом плане.

Пылаева Н. М., Ахутина Т. В. Методика «Сложи фигуру» в диагностике и коррекции зрительно-пространственных трудностей // Школа здоровья, 2000. – № 3.

Глава 4

Настольные и компьютерные игры для преодоления пространственных трудностей у детей с церебральным параличом[3]

Отставание в развитии пространственных функций может быть как проявлением незрелости или поражения определенных мозговых структур, так и вторичным следствием нарушений, ведущих к ограничению автономного освоения пространства (Foreman, Orencas, Nicholas, Morton & Gell, 1989; Stanton, Wilson, Foreman, 1996). Недостаточное развитие навыков перемещения, навигации, зрительно-моторной координации может влиять на развитие других пространственных функций, например на ориентацию в ближнем пространстве (Foreman, Orencas, Nicholas, Morton & Gell, 1989; Stanton, Foreman & Wilson, 2002). И наоборот, развивающее обучение, направленное на коррекцию одних пространственных функций, может вести к улучшению других (Kass & Ahlers, 1998; Snodgrass, 2000).

У детей с детским церебральным параличом (ДЦП) дефицит пространственных функций особенно выражен, однако специальная коррекционная работа по развитию пространственных функций, как правило, не ведется. Она включена в общий комплекс медицинских и психолого-педагогических форм работы с детьми (Левченко, Приходько, 2001; Финни, 2001).

Развитие современных компьютерных технологий открыло новые перспективы для разработки специальных реабилитационных средств, позволяющих работать с детьми с тяжелыми поражениями двигательной сферы. Создаваемая компьютером среда виртуальной реальности (СВР) позволяет совершать воображаемые «путешествия в пространстве» тем, кто лишен возможности физического перемещения. Исследования показывают, что опыт пространственной тренировки с использованием СВР переносится на реальную среду детьми группы нормы и с отклонениями в развитии (McComas, Pivik & Laflamme, 1998; Rose & Foreman, 1999; Stanton, Wilson, Foreman, 1996; Stanton, Foreman & Wilson, 2002). При этом было обнаружено, что дети, которые не могут сами владеть компьютерной мышью или джойстиком, могут получать пространственную информацию с экрана компьютера, если управляют виртуальными движениями с помощью команд, даваемых экспериментатору (Wilson, 1997). Все это говорит о широких возможностях использования СВР в коррекционно-развивающей работе с детьми, имеющими проблемы психомоторного развития.

Наше исследование было нацелено на проверку того, как разработанный нами комплекс компьютерных и поддерживающих настольных методик способствует развитию ориентации в пространстве (как эгоцентрической, так и аллоцентрической) и влияет ли он на улучшение других видов пространственных функций детей, страдающих ДЦП. Этот комплекс реабилитационных методик, а также тесты для измерения результатов работы были ориентированы на детей не только со средними, но и с тяжелыми формами церебрального паралича, самостоятельное перемещение которых сильно затруднено и навыки ориентации в «большом» пространстве и координации в «малом» пространстве недостаточно развиты. Среди них могли быть и «безречевые» дети, для успешной работы от них требовался минимум: возможность подачи словом или взором, движением головы пяти команд. Все операции для реализации этих команд выполнял оператор-тренер.

Исследование включало пилотажную и основную части. В первой, пилотажной, части апробировался набор только компьютерных методик. Пилотажный эксперимент позволил прийти к следующим выводам.

1. Предложенные коррекционные методики действительно развивают пространственные функции у детей, хотя они эффективны лишь при наличии определенного стартового уровня освоения пространства.

2. Необходимо разработать предваряющие компьютерный комплекс задания, которые готовили бы детей с наиболее выраженными отклонениями к решению зрительно-пространственных задач (Ахутина, Кричевец, 2002).

Остановимся подробнее на второй, основной части эксперимента.

Все дети находились на лечении в Республиканском объединении по реабилитации и восстановительному лечению детей-инвалидов (Горки Ленинские) с диагнозом «Детский церебральный паралич». В эксперименте принял участие 51 ребенок в возрасте от 8 до 14 лет. После клинического обследования и предварительного собеседования дети разбивались на пары с близкими результатами и из каждой пары один ребенок отбирался в экспериментальную группу, а второй в контрольную. 6 детей выписались из стационара досрочно. В связи с этим полные данные собраны по 23 детям экспериментальной группы и по 22 – контрольной. В обеих группах были дети с диплегией, левосторонним гемипарезом, правосторонним гемипарезом и атонической-астатической формой ДЦП (в экспериментальной группе соответственно 13-2-1-1, в контрольной – 14-6-1-1). Только в экспериментальной группе было 3 ребенка с гиперкинетической формой ДЦП. Дети-колясочники (2 ребенка) были представлены только в экспериментальной группе.

Дети обеих групп проходили стандартный курс реабилитации (фармакологическое лечение, лечебная гимнастика и т. п.), а экспериментальная группа дополнительно занималась по экспериментальной методике. С каждым ребенком проводились занятия 2–3 раза в неделю в течение 5 недель, занятия длились 30–60 мин. До и после курса дети проходили тестирование пространственных функций, осуществляемое с помощью разработанных нами компьютерных методик и тестов, входящих в нейропсихологическое обследование (см. ниже). Полное нейропсихологическое обследование детей и тестирование по матрицам Равена проводили однократно в начале обучения.

Курс коррекционно-развивающего обучения был разработан по методологии Л. С. Выготского – А. Р. Лурия (см. выше). Он начинался с подготовительных игр и заданий. После пятого занятия параллельно подключались компьютерные игры. Количество поддерживающих занятий зависело от успешности прохождения их программы, всего ребенок получал от 5 до 10 тридцатиминутных занятий. Количество компьютерных занятий также зависело от скорости освоения игровых заданий и составляло в среднем 8 занятий. Все тестовые и коррекционные занятия проводились индивидуально в отдельной комнате.

Поддерживающие задания. Целью таких заданий было закрепление пространственного словаря и развитие речевой регуляции пространственных действий, то есть развитие собственно пространственных функций и функций программирования и контроля, необходимых для решения пространственных проблем. При выполнении этих заданий вводились (или тренировались) понятия «верх», «низ», «вперед», «назад», «вправо», «влево» с эгоцентрической точки зрения, а также совмещение понятий «верхний правый угол» и т. п. Отдельно отрабатывались команды движения: «вперед», «стоп», «поворот направо» и т. п.

Все игры были упорядочены так, чтобы обеспечивать постепенное повышение нагрузки на пространственные функции и регулирующую функцию речи. Дидактический материал широко варьировался с целью поддержания интереса детей к заданиям. В набор входили игры: «Полет воздушного шара (бабочки)», «Почтальон» (игры реализованы на металлическом планшете); «Сложи фигуру» (фигуры складываются из карточек, деталей «Лего», деревянных панелей из методики «Черные квадраты»); графические диктанты, «Учитель-робот». Каждая игра-задание позволяла широко варьировать набор выполняемых действий.

Так, в заданиях «Сложи фигуру» дети проводили:

¦ анализ рамки и образца, построение фигур по образцу и по памяти;

¦ поиск образца меньшего размера;

¦ выстраивание фигуры по образцу меньшего размера;

¦ обведение контура фигуры, раскрашивание фигуры;

¦ складывание фигуры из элементов меньшего размера;

¦ графическое воспроизведение рамки и образца меньшего размера на листе в крупную клетку.

Кроме того, дети работали с набором бланковых методик разного уровня сложности на узнавание, копирование, воспроизведение по образцу и по памяти различных пространственных структур (отдельные задания и их комплексы представлены выше).

Компьютерные развивающие игры. Компьютерные задания демонстрировались на стандартном компьютере IBM-PC. Они были разработаны с помощью пакета программ Superscape. Дети смотрели на экран монитора размером 40 х 30 см с удобного расстояния около 40 см. Движения в виртуальном пространстве (вперед, назад, повороты вправо и влево) производились тренером по команде испытуемого. Все движения производились с небольшой постоянной скоростью и прекращались по команде ребенка «стоп». Предметные копии лабиринтов (см. ниже) конструировались из снабженных магнитами пластиковых фишек (стен), помещенных на металлическую поверхность размером 40 х 40 см.

Идея комплекса компьютерных методик состояла в моделировании одних и тех же пространственных задач (лабиринтов) различными средствами для постоянного соотнесения в процессе работы пространственных структур, выполненных в разном материале с тем, чтобы получить обобщенный навык работы с пространственными структурами данного вида. Детям предлагали следующие задания:

¦ компьютерный двумерный лабиринт;

¦ изготовление «игрушечной» (предметной) копии лабиринта и продвижение по нему;

¦ виртуальный трехмерный лабиринт, движение в котором осуществлялось с опорой на предметную копию. (Все три варианта реализовывали лабиринт одной и той же структуры.)

Целью ребенка было достижение находящегося в лабиринте «дерева» (нарисованного, игрушечного или виртуального).

В первом и втором заданиях по лабиринту продвигалась «божья коровка», нарисованная или игрушечная.

В третьем задании в виртуальном пространстве двигалась «точка зрения» играющего. В первом и втором случаях лабиринт виделся сверху и цель была видна. В последнем задании виртуальная точка зрения перемещалась по горизонтали ниже верхней кромки стен лабиринта. Стены лабиринта загораживали низкое дерево, и оно становилось видимым только в непосредственной близости от него. Ребенок подавал тренеру команды «вперед», «стоп», «направо», ориентируясь на их (ребенка и тренера) общую точку зрения. При перемещении «божьей коровки» команда «направо» интерпретировалась как поворот на месте в сторону ее правой передней ноги. Это было сделано с той целью, чтобы унифицировать команды во всех трех видах заданий и не допустить множественности интерпретаций.

Занятие начиналось с двумерной компьютерной игры – ребенок двигал «божью коровку» к видимому дереву. После этого он строил модель этого лабиринта из пластиковых полосок с магнитами и двигал игрушку к выходу. Наконец, дети решали задачу виртуального перемещения и достижения цели с опорой на реальную модель. Структура лабиринта, единая во всех трех заданиях, постепенно усложнялась в ходе курса коррекции (примеры лабиринтов в двумерной игре представлены на рис. 4.4.1).

Имелось также дополнительное задание, предлагавшееся тем ученикам, которые прошли полный цикл лабиринтов. Оно состояло из 6 вариантов виртуального парка, в определенной точке которого была спрятана цель (маленький вращающийся ветряк). Цель находилась в яме и была видна только с минимального расстояния. К каждому из вариантов задания прилагалась карта «парка» с помеченным местом нахождения цели и местами нахождения двух крупных ориентиров, видимых из любой точки «парка». Стартуя от произвольной точки, ученик должен был найти спрятанную цель (подробнее о методике работы см.: Ахутина, Кричевец, 2002; Ахутина, Форман и др., 2004; Akhutina, Foreman et al., 2003).

Рис. 4.4.1. Примеры двумерных лабиринтов. Слева – простой лабиринт, справа – лабиринт средней сложности

Чтобы оценить эффективность коррекционного воздействия, были использованы два специально разработанных компьютерных теста и нейропсихологические пробы, не требующие графической деятельности.

До курса коррекции для сравнения детей основной и контрольной групп им предлагали тест «Матрицы Равена».

В комплект инструментария, применяемого с помощью компьютера, входили следующие методические средства.

Компьютерный вариант методики «Кубики Кооса». В правой половине экрана тестируемому предъявлялась конфигурация, составленная из трех видов квадратов: сплошного белого; сплошного красного; поделенного диагональю на красную и белую половины.

Такие же квадраты были представлены в нижней части левой половины экрана.

Цель задания – составить аналогичную конфигурацию в левой части экрана. Тестируемый мог давать команды «вверх», «вправо», «влево», «вниз», «повернуть», «сменить фигуру». Поворот осуществлялся по каждой команде на 22,5° в любую сторону.

Задания делились по сложности на 4 группы по следующим признакам:

¦ границы квадратов совпадают/не совпадают с границами цветовых полей;

¦ стороны квадратов параллельны/расположены под углом 45° к границам экрана.

Выполнение задания оценивалось с помощью 5 шкал, отражающих передачу общего гештальта, ориентацию основных частей относительно экрана, наличие зазоров между квадратами и т. п. По каждой шкале ребенок получал 0 (правильно)– 2 (полностью неправильно) балла.

Компьютерное задание на конструктивный праксис. На экране показывали два изображения клоуна, симметричные относительно вертикальной оси экрана. Тестируемому предлагалось запомнить клоуна и его «отражение». Через минуту левое изображение убиралось, а в нижней части левой половины экрана располагались детали изображения (руки, туловище, ноги и шляпа), причем ноги и руки предлагались в двух ориентациях (задаваемых положением кисти и стопы). Фигуры передвигались теми же командами, что и в предыдущем задании (на рис. 4.4.2 представлены результаты одного из испытуемых по этому тесту).

Выполнение задания также оценивалось с помощью 5 шкал, отражающих передачу общего гештальта, ориентацию основных частей тела, углы наклона частей клоуна, ориентацию рук и ног, расстояние между прилегающими элементами. Оценки по каждой шкале ребенок получал от 0 до 2 баллов.

Оценка выполнения тестов производилась экспертами, не знающими, к какой группе относится ребенок.

Нейропсихологические пробы включали следующие методические средства.

Тест Бентона на ориентацию линий (Benton, Hamsher, Varney and Spreen, 1983) оценивает пространственное восприятие. Тест включает 5 наклонных отрезков. Испытуемый должен найти линию с таким же наклоном на контрольной карте. Количество сегментов между выбранной ребенком линией и правильной определяет штрафной балл. Общая оценка – сумма отдельных оценок.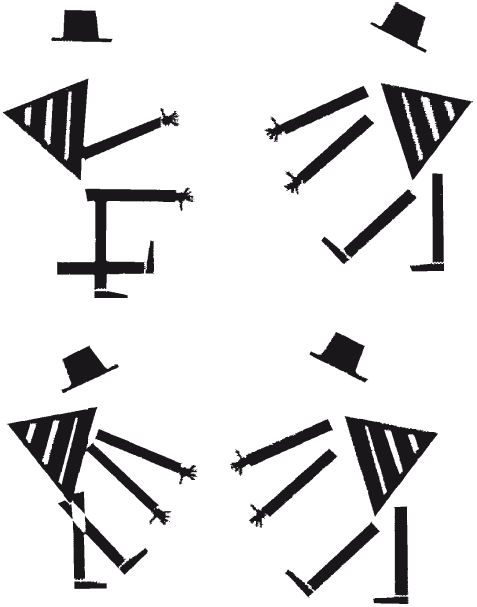

Рис. 4.4.2. Образец (справа) и выполнение (слева) компьютерной пробы на конструктивный праксис: «клоун» до (вверху) и после (внизу) прохождения коррекционного курса

Субтест «Стрелы» из нейропсихологической батареи для детей Nepsy (Korkman, Kirk & Kemp, 1998) также требует оценки ориентации линий. В каждом задании на бланке изображены 8 стрелок и цель. Нужно определить, какая стрелка направлена на цель (их две). Оценка – количество правильно найденных стрелок (максимум 10).

«Дорожки» – тест, разработанный в Институте дошкольного образования АО СССР и включенный в Nepsy. Тест измеряет восприятие зрительно-пространственных отношений и возможность пользоваться схемами маршрута. Оценивалось количество правильных ответов (максимум 10).

Группы не отличались друг от друга по полу (52 % мальчиков в экспериментальной и 55 % в контрольной группе) и по возрасту (m = 9,7, s = 1,6 в основной и m = 9,7, s = 1,6 в контрольной группах). Не было найдено различий при оценке интеллекта с помощью матриц Равена. Данные по пространственным пробам до и после прохождения курса коррекции были нормализованы по первичным данным для использования в статистическом анализе. Различий между группами в состоянии пространственных функций до коррекции обнаружено не было.

Корреляционный анализ показал существенную негативную корреляцию между состоянием пространственных функций до прохождения курса реабилитации и улучшением этого показателя за время эксперимента у испытуемых обеих групп в совокупности (r = -0,51, p < 0,001). Диаграмма рассеяния представлена на рис. 4.4.3. Для контроля этого фактора переменная «стартовый суммарный показатель тестирования пространственных функций» была включена в качестве ковариаты в дисперсионный анализ. Был использован дисперсионный анализ (ANOVA) с зависимой переменной «улучшение суммарного показателя тестирования», фактором «экспериментальная/контрольная группа» и описанной выше ковариатой. Обе группы продемонстрировали улучшение результатов: t-критерий показал для контрольной группы: t = 5,71, df = 21, p < 0,001, для экпериментальной группы: t = 8,65, df = 22, p < 0,001, но прогресс экспериментальной группы был значительно выше (ANOVA, F = 5,35, p = 0,026).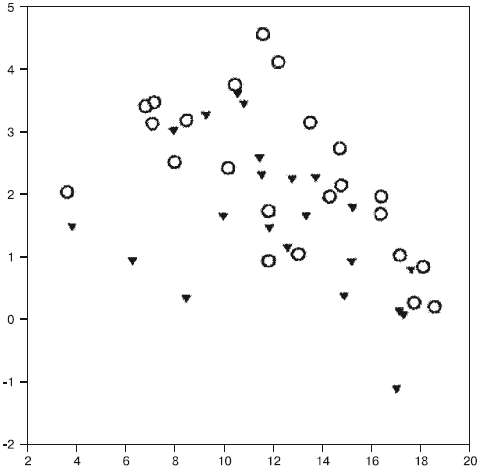

Рис. 4.4.3. Диаграмма рассеяния результатов испытуемых: по горизонтальной оси результаты тестирования в начале эксперимента, по вертикальной – разность между результатами тестирования в начале и в конце эксперимента; О – экспериментальная группа; Ў – контрольная группа

Исследование показало, что пространственные функции детей с моторными нарушениями могут быть улучшены при использовании разработанной батареи заданий. Результаты находятся в соответствии с более ранними наблюдениями, которые показывают, что для детей и взрослых навигационный опыт, получаемый в виртуальной среде, особенно эффективен в отношении развития пространственных функций (Foreman, Stirk, Pohl, Mandelkow, Lehnung, Herzog & Leplow, 2000; Foreman, Stanton, Wilson & Duffy, 2003; McComas, Pivik & Laflamme, 1998; Stanton, Wilson, Foreman, 1996). Вполне возможно, что соединение тренинга в СВР с более традиционными настольными пространственными играми и поддерживающими заданиями ведет к улучшению пространственных функций в целом, обнаруженному у детей экспериментальной группы.

В отличие от пилотажного эксперимента (в котором дети с низким уровнем развития пространственных и регуляторных функций не были успешны в освоении компьютерных навигационных игр), в основном эксперименте прогресс обнаружен у всех детей, и он был особенно большой у детей с низким стартовым уровнем (что обнаруживает высокая отрицательная корреляция между исходным уровнем и улучшением). Благодаря дополнительным поддерживающим заданиям всем детям удалось интериоризовать пространственные понятия и успешно действовать в новой среде. Их успех отражает оптимальность интерактивного обучения и эффективность методов, построенных на основе методологии Выготского – Лурия.

Как в пилотажном, так и в основном экспериментах все дети проходили стандартный курс коррекции, неудивительно поэтому, что улучшение тестируемого показателя наблюдалось в обеих группах, но в экспериментальной группе оно было значительно выше. Этот факт – отчетливое свидетельство полезности предложенного курса коррекции.

У нас есть только ограниченные данные об улучшении общего функционирования ребенка после прохождения коррекционных занятий, хотя полученные нами неформальные данные от педагогического персонала, медсестер и родителей говорят о позитивном влиянии проведенного тренинга на школьные успехи детей. До какой степени тренинг пространственных функций оказывает влияние на общие жизненные навыки и овладение школьными знаниями – этот вопрос заслуживает специального рассмотрения.

1. Ахутина Т. В., КричевецА.Н. Использование виртуальных сред для развития пространственных функций у детей с церебральным параличом // Вестник Московского университета. Серия 14. Психология, 2002. – № 4. – С. 77–85.

2. Ахутина Т. В., Форман Н., Кричевец А. Н., Матикка Л., Нархи В., Пълаева Н. М., Вахакуопус Е. Развитие пространственных функций у детей с церебральным параличом с помощью компьютерных и настольных игр // Школа здоровья, 2004. —№ 4. – С. 30–37.

3. Левченко И. Ю., Приходько О. Г. Технологии обучения и воспитания детей с нарушениями опорно-двигательного аппарата. – М., 2001.

4. Финни Н. Р. Ребенок с церебральным параличом. Помощь, уход, развитие. Книга для родителей. – М., 2001.

5. Akhutina Т., Foreman N., Krichevets A., Matikka L., Narhi V., Pylaeva N., VahakuopusJ. Improving spatial functioning in children with cerebral palsy using computerized and traditional game tasks // Disability and Rehabilitation, 2003. – Vol. 25. —N. 24. – Р. 1361–1371.

6. Benton A.L., Hamsher K., Varney N. R. and Spreen O. Contributions to neuropsychological assessment. – New York: Oxford University Press, 1983.

7. Foreman N. P., Orencas C., Nicholas E., Morton P. & Gel M. Spatial awareness in seven to eleven year-old physically handicapped children in mainstream schools // European Journal of Special Needs Education, 1989. – P. 4, 171–179.

8. Foreman N., StirkJ., PohlJ., Mandelkow L., Lehnung M., Her-zogA. & Leplow B. Spatial information transfer from virtual to real versions of the Kiel Locomotor Maze // Behavioural Brain Research, 2000. – P. 112, 53–61.

9. Foreman N., Stanton D., Wilson P. &Duffy H. Spatial knowledge of a real school environment acquired from virtual or physical models by able-bodied children and children with physical disabilities // Journal or Experimental Psychology: Applied, 2003. – P. 9, 67–74.

10. KassS. & Ahlers R. Eliminating gender differences through practice on spatial skills in girls and boys //Journal of Applied Developmental Psychology, 1998. – P. 15, 13–32.

11. Korkman M., Kirk U. &KempS. NEPSY. A developmental neuropsychological assessment. – San Antonio, TX: The Psychological Corporation, 1998.

12. McComas J., Pivik J. & Laflamme M. Children's transfer of spatial learning from virtual reality to real environments // Cyberpsychology and Behavior, 1998. – P. 1, 121–128.

13. Rose D. & Foreman N. Virtual Reality // The Psychologist, 1999. – P. 12, 550–554.

14. Snodgrass L. Imagery training improves both spatial skills and graph reading. Paper presented at the 27^th International Congress of Psychology, Stockholm, Sweden. – July, 2000.

15. Stanton D., Wilson P., Foreman N. Using virtual reality environments to aid spatial awareness in disabled children // In: Sharkey P.M. (ed.) Proceedings of the 1-st European conference on disability, virtual reality and associated technologies, Maidenhead, Berkshire. – UK, 1996. – P. 93–101.

16. Stanton D., Foreman N. & Wilson P. Effects of early mobility on shortcut performance in a simulated maze // Behavioural Brain Research, 2002. – P. 136: 61–66.

17. Wilson P. N. Virtual Reality in spatial research // N. Foreman & R. Gillett (Eds.), Handbook of Spatial Research Paradigms and Methodologies. – Vol. 1: Spatial Cognition in the Child and Adult. Hove: Psychology Press, 1997.

В данной главе представлены 12 типичных заданий, которые показывают разработанную нами последовательность направлений работы по развитию и коррекции зрительно-пространственных функций с детьми-дошкольниками.

Задание 1. Ориентировка в пространстве листа.

На листе бумаги ребенку предлагают найти середину (центр) листа и нарисовать шарик. Далее ему дают задание: «Шарик летит вверх – прочерти дорожку и нарисуй шарик вверху».

Аналогично с ребенком отрабатывают положения внизу, слева и справа.

Затем шарик летит в верхний левый угол, верхний правый угол и т. д. (рис. 4.5.1).

В следующий раз ребенка просят нарисовать бабочку, листочек и по инструкции сделать то же самое.

После этого можно перейти к более сложному рисунку. «Нарисуй внизу травку, в левом нижнем углу – грибок; вверху – облака, в верхнем правом углу – солнышко».

Задание 2. Лабиринт.

Сначала ребенок помогает ежикам найти в лабиринте путь к яблокам, проводя дорожку пальчиком. Затем он рисует ее простым карандашом и исправляет ошибки, если они есть (стирает ластиком), потом обводит цветным карандашом, диктуя ежикам команды: вверх, вниз, направо, налево (рис. 4.5.2).

Задание 3. Освоение листа в клетку.

На листе в клетку ребенку предлагают найти середину и обвести одну клеточку. Потом он обводит клеточку в середине, в верхней, нижней, левой, правой части листа, а затем в левом верхнем уголке и т. д. (рис. 4.5.3).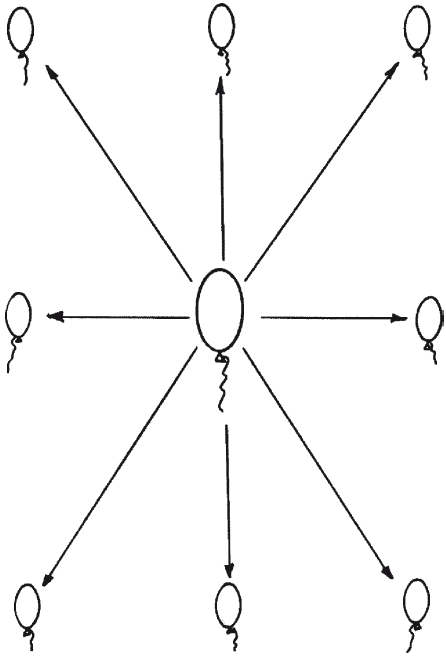

Рис. 4.5.1. К заданию 1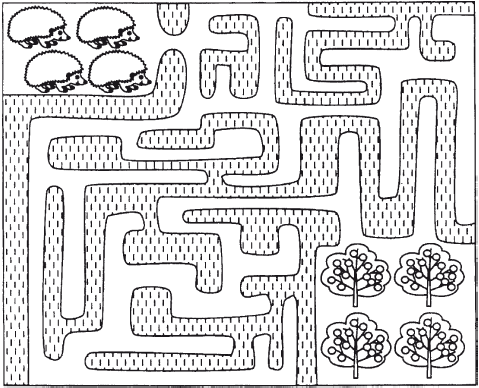

Рис. 4.5.2. К заданию 2

Затем отрабатываются движения в разных направлениях. Сначала «сажаем морковку» – проводим линии от заданных точек на 1, 2 и т. д. клетки вниз. Затем «выращиваем цветы» – линии от точек вверх, далее «забиваем гвоздики» – линии направо и налево.

После этого учимся обозначать длину пути и направление движения: ставим число и соответствующую стрелку. Предлагаем прочитать запись: «2>, то есть две клетки направо» и т. д. Это готовит детей к выполнению графического диктанта.

На следующих занятиях ребенку предлагаются усложняющиеся программы действий:

¦ продолжить узор по заданной программе с опорой на образец;

¦ выполнить узор по заданной программе;

¦ проанализировать образец и составить программу (эти задания могут быть разной сложности). Все программы проговариваются, например: «Одна клетка вверх, две направо…».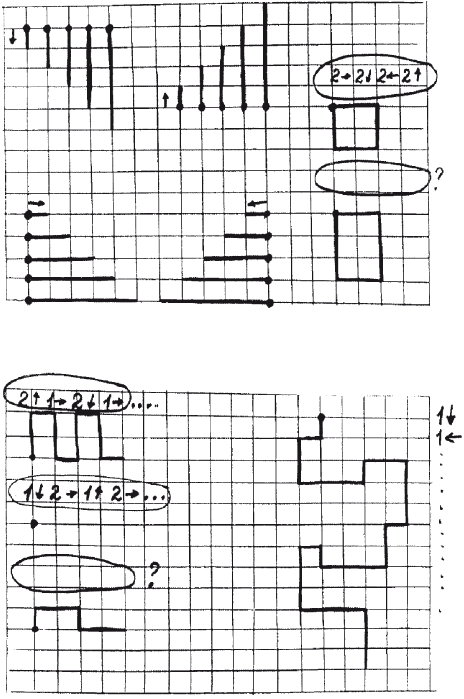

Рис. 4.5.3. К заданию 3

Задание 4. Графические диктанты. («Гномы приглашают гостей».)

Это задания из пособия по подготовке детей к школе «Скоро школа. Путешествие с Бимом и Бомом в страну Математику» (Ахутина, Манелис, Пылаева, Хотылева, 2006).

Первый графический диктант выполняется по программе, которую проговаривает взрослый (ребенок не только видит программу, но и слышит ее). Каждый выполненный шаг программы отмечается цветным маркером.

Следующие задания ребенок выполняет самостоятельно, диктуя себе шаги вслух или про себя. Пройденный шаг маркируется в программе (рис. 4.5.4).

Задание 5. Копирование рисунков по клеткам.

Выполнению этих заданий предшествует работа по делению клеток пополам вертикальными, горизонтальными и диагональными линиями. Параллельно отрабатывается складывание квадрата из 2 или 4 соответствующих частей.

В первом задании взрослый помогает ребенку проанализировать чертеж. Они вместе последовательно проговаривают направление движения и количество клеток, и ребенок воплощает эту программу.

Второе задание ребенок выполняет самостоятельно (рис. 4.5.5).

Задание 6. Варианты работы с рисунками по клеткам. Желательно, чтобы ребенок научился разнообразным способам выполнения заданий:

¦ взрослый диктует, а ребенок выполняет рисунок по речевой программе;

¦ ребенок выполняет рисунок по зрительному образцу;

¦ ребенок анализирует рисунок и составляет программу, а потом диктует другому ребенку или взрослому (рис. 4.5.6).

Задание 7. Структуры точек.

Задания со структурами точек используются и для отработки пространственных функций, и для развития функций программирования и контроля (см.: «Школа внимания», Пылаева, Ахутина, 2003) (рис. 4.5.7).

Рис. 4.5.4. К заданию 4

При работе по развитию пространственных функций взрослый предлагает ребенку:

Рис. 4.5.5. К заданию 5

¦ обвести кружки на кружках, сосчитать их количество и обсудить их расположение;

¦ соотнести одинаковые структуры на кружках и ложках и провести дорожку от кружки к ложке;

¦ сравнить, одинаково ли украшены кружки и тарелки с одним и двумя кружками;

¦ разрисовать тарелки, повторяя рисунок на кружках.

Задание 8. «Бим и Бом проводят „научное исследование“ цифр».

В этом задании обсуждается строение цифр, дети обводят цифры и самостоятельно конструируют их из пластилина или теста.

Для преодоления зеркальности полезно выстроить цифры в ряд, выделить начало написания каждой цифры и «открыть», что только цифра 6 смотрит направо, отвернувшись от цифры 5 (рис. 4.5.8).

Рис. 4.5.6. К заданию 6

Задание на дорисовывание достаточно сложное. Сначала цифры дорисовываются простым карандашом, чтобы можно было исправить ошибки.

Задание 9. «Узнай и допиши букву».

Работа с буквами способствует развитию зрительно-пространственных функций. С этой целью используется конструирование букв из элементов. Внимание ребенка обращают на то, какие буквы можно построить из палочек, а для каких нужны округлые элементы. Самые простые буквы складываются из палочек разного размера, и с самого начала для профилактики зеркальных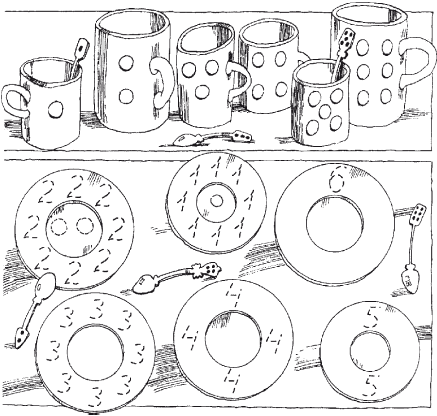

Рис. 4.5.7. К заданию 7

ошибок важно фиксировать пространственное расположение буквы в целом и ее элементов. Не вызывают трудностей симметричные буквы: «А», «Д», «Ж», «Л», «М», «Н», «О», «П», «Т», «Ф», «Х», «Ш». Зеркальные ошибки (справа – слева) встречаются в 11 буквах, которые смотрят направо: «Б», «В», «Г», «Е», «К», «Р», «С», «Ь», «Ы», «Ъ», «Ю», и в 5 буквах, которые смотрят налево: «З», «У», «Ч», «Э», «Я», а также в букве «И».

В задании сверху представлены гласные и согласные, опираясь на которые ребенок может разгадать зашифрованные слова. Ребенок вместе со взрослым приходит к выводу, что в этом наборе у букв не хватает левых частей. Далее он выбирает любимый цветной фломастер и, разгадывая букву за буквой, дорисовывает недостающие элементы и читает все слово. После выполнения нескольких таких заданий, где он дополняет так же правые,

Бим и Бом стали вспоминать, с какими цифрами они познакомились в стране Математике.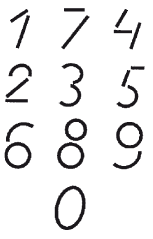

Мальчики заметили, что есть цифры, которые состоят только из палочек. Обведи их.

Есть цифры, которые состоят из палочек и половинок круга. Обведи их.

Есть цифры, которые состоят из кругов и крючочков. Обведи их.

А еще есть цифра, непохожая на все остальные. Она – в виде овала.

Бим и Бом решили из страны Математики уплыть на корабле. Но перед отплытием надо было оставить что-нибудь вкусное для цифр. Помоги Биму и Бому вылепить печенье для каждой цифры. Дорисуй их. Какой цифре не хватило печенья? Нарисуй недостающее печеньице.

Рис. 4.5.8. К заданию 8

нижние или верхние половинки букв, ребенок сам зашифровывает слова для педагога или других детей (рис. 4.5.9).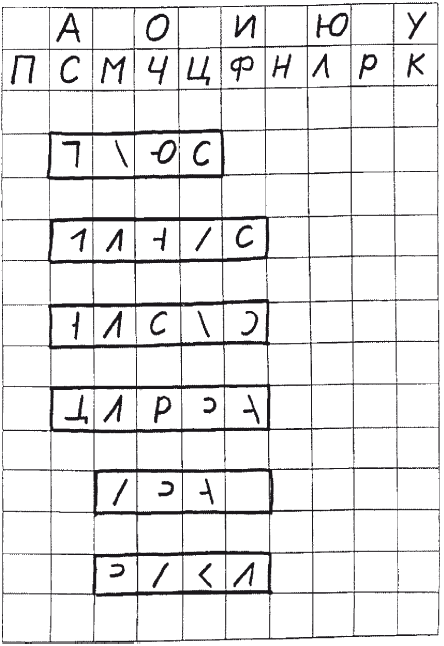

Рис. 4.5.9. К заданию 9

Задание 10. Римские цифры.

Работа с римскими цифрами позволяет отрабатывать и состав числа, и значимость позиций слева и справа.

Взрослый рассказывает про римские цифры, пользуясь текстом и картинкой.

Римские цифры показываются на пальцах и выкладываются из палочек. Особое внимание обращается на «5» и «10» и их соседей.

Далее римские цифры обводятся и соотносятся с арабскими (рис. 4.5.10).

Задание 11. Задачи на наглядное зрительно-пространственное мышление.

Ребенок вместе со взрослым рассматривает ковер, перечисляет, каких частей не хватает («и верхнего левого угла, и верхнего правого…»). Выделяет слово «влево» и раскрашивает его и узоры, которые смотрят влево, синим цветом. Далее находит такой же узор на кусочках и раскрашивает его. Потом определяет, какой кусочек подходит для левого верхнего угла, и соединяет их дорожкой, также находится кусочек для левого нижнего угла. Слово «вправо» и соответствующие узоры раскрашиваются красным, а затем рисуются дорожки. В центральном кусочке сначала раскрашиваются соответствующим цветом узоры, направленные влево и вправо, а затем узор, смотрящий вверх (на солнце), – желтым, а смотрящий вниз (на траву) – зеленым.

Во второй части ребенок решает логические задачи на основании понятий «влево-вправо», «вверх-вниз» (рис. 4.5.11).

Задание 12. Понимание обратимых конструкций с предлогами.

Это задание – пример работы над квазипространственными функциями (рис. 4.5.12).

Взрослый рассказывает, что в сарае прячется какой-то зверек.

«Сначала он спрятался там, где НА ящике стоит бочка (поставь в этом месте точку и цифру 1). Потом он перебежал туда, где ящик лежит В бочке (поставь здесь точку и цифру 2). Затем туда, где ящик ЗА бочкой (поставь здесь точку и цифру 3). Потом туда, где ПОД ящиком бочка (поставь здесь точку и цифру 4). А потом туда, где ящик ПЕРЕД бочкой (поставь здесь точку и цифру 5). Теперь соедини точки по порядку. Что у тебя получилось? (Звезда.) А чего в ней не хватает? Проведи недостающую линию».

В древние времена люди пользовались для счета пальцами, поэтому римские цифры похожи на пальчики. Обрати внимание, как при помощи рук изображаются числа пять и десять – ведь на одной руке 5 пальцев, а на двух – 10. Посмотри на рисунки и обведи римские цифры. В квадратики впиши соответствующие арабские цифры.

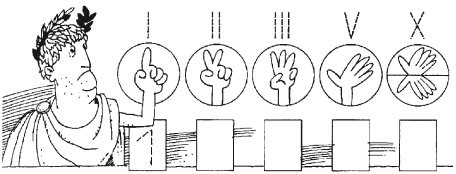
Посмотри, как записываются римские цифры, и обведи их.

Под каждой римской цифрой напиши соответствующую ей арабскую.

Рис. 4.5.10. К заданию 10

На этом материале можно отрабатывать и употребление предложных конструкций.

Взрослый говорит: «Я положил яблоко в бочку на ящике. Найди. А теперь я переложил его – угадай куда?»

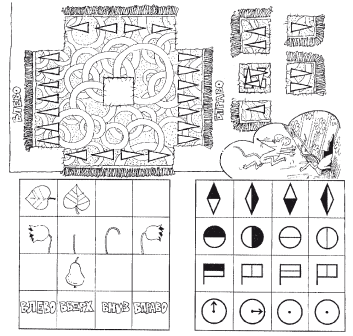Рис. 4.5.11. К заданию 11

Рис. 4.5.12. К заданию 12

Глава 6

Взаимодействие педагога и нейропсихолога при разработке методического пособия «Состав числа»[4]

При творческом взаимодействии нейропсихологов с педагогами появляется возможность применения нейропсихологического подхода в коррекционно-развивающем обучении. Для этого необходимо создание новых блоков обучающих методик, предназначенных для облегчения усвоения учебной программы. В разработке таких дидактических материалов особенно важно участие педагогов, так как последние знают учебные программы и обладают богатым арсеналом методов по развитию познавательной активности детей. Опыт показывает, что совместная работа педагога и нейропсихолога создает условия для предупреждения школьной неуспеваемости.

Мы выбрали для разработки тему «Состав числа» по следующим причинам. Эта тема является одной из самых важных и самых сложных в программе начальной школы. Несмотря на большое количество методической литературы, касающейся данной темы, она продолжает оставаться трудной для большинства детей. Неусвоенный материал данной темы не дает ребенку возможности для успешного прохождения дальнейшей программы (автоматизация вычислительных навыков в пределах 10, сложение, вычитание чисел с переходом через десяток и т. д.).

Методическая литература по данной теме недостаточно учитывает различные трудности детей, и потому учитель не может в полной мере воплотить системный подход к освоению этого материала. Мы выделили следующие трудности детей при усвоении темы «Состав числа».

Зрительные и зрительно-пространственные:

¦ трудности ориентации на листе;

¦ трудности опознания, запоминания и актуализации пространственных структур;

¦ зеркальность;

¦ трудности работы в зрительно-насыщенном поле;

¦ трудности соотнесения числа с количеством. Программирование и контроль:

¦ неумение ориентироваться в задании, построить программу работы;

¦ невозможность выполнения развернутой программы, необходимость пошагового планирования извне;

¦ импульсивность или инактивность действий;

¦ трудности контроля – трудности проверки без внешних программ;

¦ трудности серийной организации – установления последовательности действий;

¦ трудности переноса способов действия.

Из анализа трудностей детей вытекают требования к построению системы методов формирования представлений о составе числа:

¦ необходимость условий, повышающих мотивацию к обучению (разнообразные, в том числе игровые, формы работы), повторение, не повторяясь;

¦ градация трудностей и организация пошагового усвоения с вынесенной программой действий, обеспечение постепенного перехода от предметного действия к выполнению заданий в уме;

¦ учет пространственного фактора, необходимость репрезентации количества в определенных структурах;

¦ учет зрительного фактора – ранжирование насыщенности зрительного поля.

Наше методическое пособие представляет собой пакет бланковых методик, построенных на основании выдвинутых требований. Здесь мы демонстрируем примеры заданий на усвоение числа «три».

Три – одна из самых простых для восприятия структур количества, ее легко определить на глаз даже маленькому ребенку. Чтобы научить ребенка считывать разнообразные структуры, мы решили представить состав числа «три» в четырех различных по пространственной ориентации вариантах. Это делает задания более интересными, дает ребенку возможность научиться анализировать зрительный материал, ориентироваться на листе, развивать зрительное восприятие и зрительно-пространственные представления.

Бланки 1, 2 (рис. 4.6.1) предполагают следующие виды заданий: обведение структур, выкладывание их из пластилина, мозаики, пуговиц, копирование структур с данного образца. Это первый уровень сложности, на котором ребенок действует по развернутой программе. На первом этапе от ребенка не требуется удержания структуры (программы) в памяти, у него есть возможность пошагового выполнения задания.

Рис. 4.6.1. Бланки 1 и 2

Бланки 3, 4, 5 предполагают узнавание и воспроизведение структур. Бланк 3 – узнавание структур точек с опорой на образец. Бланк 4 – воспроизведение структур точек по памяти (контрольное задание) (рис. 4.6.2).

Рис. 4.6.2. Бланки 3 и 4

Бланк 5 – узнавание структур, где вместо точек выступают реальные предметы (рис. 4.6.3).

Задания такого рода предполагают удержание ребенком структуры во внутреннем плане.

На следующем уровне сложности перед ребенком ставится задача дополнения структуры до целого.

Бланк 6 (см. рис. 4.6.3) – с вынесенной программой действия. Бланки 7, 8 (рис. 4.6.4) – без нее.

Эти задания сложнее предыдущих, так как для их выполнения ребенку необходимо проанализировать предложенный рисунок, перебрать в уме возможные структуры и выбрать подходящую. В заданиях бланка 8 впервые вводится цифровое обозначение

Рис. 4.6.3. Бланки 5 и 6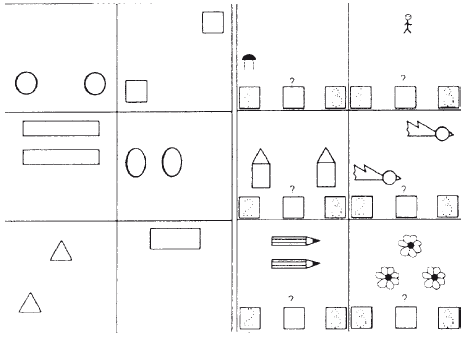

Рис. 4.6.4. Бланки 7 и 8

количества объектов без знаков действий. Оно готовит ребенка к заданиям следующего уровня сложности.

Бланк 9 (рис. 4.6.5) – контрольное задание по дополнению структуры до целого.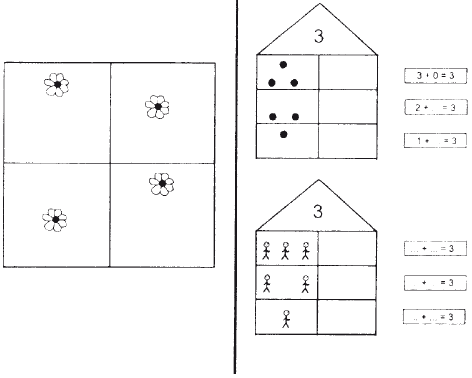

Рис. 4.6.5. Бланки 9 и 10

На бланках 10, 11, 12 даны итоговые задания. Они непосредственно выводят ребенка к активному применению полученных знаний о составе цифры «три» в арифметических действиях. На материале всех пройденных ранее видов заданий дети овладевают умением складывать и вычитать в пределах трех (рис. 4.6.6).

Данные задания апробированы при подготовке к школе детей с недостаточным развитием функций программирования и контроля и ориентировки в пространстве. Их апробация показала, что выбор материала и система предъявления адекватны возможностям детей и позволяют развивать слабые звенья высших психических функций ребенка.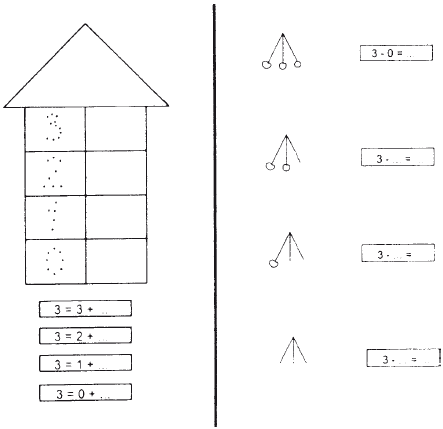

Рис. 4.6.6. Бланки 11 и 12

Трудности овладения письмом – явление нередкое в начальной школе. Они обнаруживаются в первом классе и в значительном числе случаев сохраняются и позднее, проявляясь при повышении требований к письменной речи.

Эффективное преодоление трудностей письма требует понимания их механизмов – коррекционная работа должна быть построена с учетом качественного своеобразия трудностей данного ребенка.

Нейропсихологический анализ письма, который был проведен как А. Р. Лурия (1950, 1969), так и современными отечественными и зарубежными исследователями, показывает, что в функциональную систему письма входят следующие компоненты:

¦ процессы переработки слухоречевой информации (звуковой анализ услышанного, слухоречевая память);

¦ дифференциация звуков на основе кинестетической информации;

¦ актуализация зрительных образов букв;

¦ ориентация элементов буквы; буквы, строки в пространстве;

¦ моторное (кинетическое) программирование графических движений;

¦ планирование, реализация и контроль акта письма;

¦ поддержание рабочего состояния, активного тонуса коры. Каждый из перечисленных компонентов может вызывать

трудности письма, выступая относительно изолированно или в сочетании с другими.

Пространственные трудности на письме издавна выделялись учителями. Современные исследования нейропсихологов позволяют уточнить механизм пространственных трудностей.

Ориентировка в пространстве, правильная организация действия в пространстве – сложная деятельность, в которой участвуют как правое, так и левое полушария. Самые простые, рано формирующиеся функции связаны преимущественно с работой правого полушария. От него зависят зрительно-моторные координации, возможность соотнести движение с вертикальной и горизонтальной координатами, возможность объединить в одно целое и запомнить общее взаиморасположение частей, то есть схватить целостный образ.

Левое полушарие решает более сложные задачи, особенно те из них, которые связаны с тонким анализом и речевым опосредованием. Способ его работы – анализ деталей, частей, и оно не так успешно в объединении частей в единое целое.

В данной главе мы хотели бы рассказать о трудностях письма и их преодолении у ученика 3-го (коррекционного) класса (1–3) Егора П. (имя изменено). Нейропсихологическое обследование выявило у него функциональную недостаточность правого полушария: пространственные трудности, трудности автоматизации двигательных, особенно зрительно-моторных, навыков, а также снижение функций I блока мозга, обеспечивающего нужный уровень активности, работоспособности.

Наблюдения учителя за поведением ребенка в классе показали, что в первый период Егор не хотел учиться и находиться в школе, общаться со сверстниками. Когда мальчик вовлекался в совместную работу в классе, он обнаруживал хорошее общее развитие, достаточно богатый словарь, сформированность связной речи. В то же время он был неорганизован, не умел сосредоточиться на поставленной задаче, что, вместе с отсутствием ряда учебных навыков, приводило к частым отказам от заданий, раздражительности, крайне быстрой истощаемости.

В ходе дальнейшего обучения негативные поведенческие реакции сглаживались. Мальчик стал более активным на уроках, проявлял интерес к заданиям (устным) творческого характера, у него возникла привязанность к некоторым ученикам и учителям в школе.

Выполнение письменных заданий оставалось малодоступным для мальчика. Из-за трудностей включения в задание и замедленного темпа деятельности Егор часто нервничал, торопился, начинал много зачеркивать. Иногда это заканчивалось слезами, после чего мальчик долго не мог успокоиться, говорил, что он не такой, как все, что он ничего не умеет и никогда не научится.

Колебания работоспособности в течение урока, дня сочетались с периодическими колебаниями общего самочувствия мальчика в течение недели, месяца.

Однако постепенно работоспособность мальчика возрастала, при этом она была тесно связана с повысившейся мотивацией к содержательному общению, познавательной деятельности и с осознанием своих успехов.

Обратимся теперь к работе мальчика на уроках русского языка.

Уже на первых уроках обнаружились большие «ножницы» при выполнении устных и письменных работ. При хороших знаниях орфографических правил, при умелом объяснении той или иной орфограммы мальчик практически не справлялся с письмом. Приведем образец текста, написанного под диктовку: «На корабле с нами было два мальчика» (рис. 4.7.1).

Рис. 4.7.1. Пример письма третьеклассника Егора

Анализ трудностей обнаруживает:

¦ сложности в ориентировке на тетрадном листе, в нахождении начала строки;

¦ трудности в удержании строки;

¦ буквы имеют разный наклон и высоту, элементы букв часто разрываются и не соответствуют по размеру друг другу;

¦ при написании слова с трудом вспоминается графический и двигательный образ нужной буквы, заменяются буквы, близкие по написанию: Нлассная работа, Нак все кругом, калсж (колхозный);

¦ наблюдается устойчивая зеркальность при написании букв д-в, у-ч, д-б;

¦ частое повторение слов на письме не приводит к образованию устойчивых идеограмм: Классная родота, Упрожнение, Чпражнение;

¦ часто встречается мена гласных, даже ударных, пропуск гласных: Тровка, Я сгодя хдла (Я сегодня ходила);

¦ теряется порядок букв: по…ртрпе (по тропе), део дк (декабрь);

¦ имеется тенденция к фонетическому письму: ручйи, радсно;

¦ не выделяется целостный образ слова, вследствие чего два знаменательных слова, местоимение и глагол, слова с предлогами пишутся слитно; позднее, в связи со сверхгенерализацией правила написания предлогов, пишутся отдельно приставки.

Все эти ошибки легко объясняются правополушарными трудностями обработки зрительной и зрительно-пространственной информации.

Наряду с этим на фоне утомления появились персеверации букв и слогов и контаминации слов: 24 февраа; Вена – весна; Ве Ве В поле…; На елижит – на ели лежит; Нуку немлют на мукг – муку мелют на мельнице.

Существенно отметить, что задания творческие – более сложные и одновременно более эмоционально значимые – мальчик выполнял лучше, чем простые, обычные.

Кратко остановимся на методах коррекционной работы. В соответствии с нейропсихологическим подходом Л. С. Выготского – А. Р. Лурия, основная стратегия коррекционного воздействия заключается в «выращивании» слабого звена при опоре на сильные звенья в процессе специально организованной совместной деятельности.

У Егора было два слабых звена: работоспособность и зрительно-пространственная организация акта письма. Все остальное (в частности, программирование и контроль) страдало вторично.

Чтобы увеличить работоспособность, нужно было, с одной стороны, увеличить мотивацию, заинтересованность мальчика заданием, а с другой – раздробить и уменьшить объем выполняемого задания, упростить по возможности его выполнение.

Пространственные трудности ребенка могут отрабатываться в ходе индивидуальных коррекционных занятий с психологом, но и учитель может участвовать в их преодолении.

Учитывая трудности мальчика в ориентировке на листе тетради, учитель выделял поля, а в начале даже рабочую строку. Для работы была выбрана тетрадь с разлиновкой: две строчки с редкой косой линейкой. Учитель четко давал инструкцию, где начинать писать, и проверял ее выполнение.

Программа работы по письму предполагала развернутое последовательное повторение основных орфографических правил и отработку графических навыков.

В первых заданиях учитель стремился придерживаться правила «одной трудности». Если учебная задача заключалась в усвоении содержательного грамматического правила, то графическая работа мальчику давалась минимальная – это были задания на вставку букв и слов, завершение предложений, определенные куски обычных упражнений.

Если же учебная задача заключалась в отработке графических навыков, то здесь использовалось письмо букв вместе с мнемоническим знаком для их запоминания. Например, мальчик, выполняя задание, писал букву в и рядом стрелку вверх, что позволяло упрочить правильную ориентацию буквы.

Параллельно нейропсихолог, занимаясь с ребенком, проводил «научный анализ» строчных букв. Егор выяснил, что выходят за строчку всего 7 букв: из них 2 вверх (б, в) и 5 вниз (д, з, р, у, ф); кроме того, у букв ц и щ есть маленькие хвостики (он проводил сравнение выходящих за строку элементов ц и у). Для преодоления зеркальности выделялись буквы, которые смотрят в начало и конец строки (налево и направо).

Развернутая работа над пространством шла также на уроках математики, где вначале простое написание цифр в столбик с соблюдением размеров составляло неразрешимую задачу. Чтобы преодолеть эти трудности, было изготовлено большое полотно с кармашками, которое висело рядом с доской. Когда дети решали примеры в тетрадях, Егор решал их у полотна, вставляя цифры в клетки-кармашки, что позволило ему решать сложные примеры и на сложение, и на вычитание. Снятие боязни примеров подготовило почву для записи и решения примеров в тетради, где место решения примера было расчерчено в клетку красными чернилами. Позднее необходимость в таком расчерчивании отпала.

Пространственная организация действия отрабатывалась и на уроках чтения. Для преодоления устойчивой ошибки мальчика давать наряду с левонаправленным правонаправленное чтение использовался прием слежения строки пальцем или специальной линейкой, имевшей такую форму: I___

Кроме того, регулярно проводилось чтение таблиц слогов и односложных слов. По одной таблице работали в течение месяца в начале каждого урока чтения. Дети работали попарно, читая по столбцам или строчкам, и фиксировали время чтения и ошибки. Роли учителя и ученика в паре менялись, и каждый хотел дать другому задание потруднее, а сам прочитать без ошибок. Это упражнение было направлено на узнавание слогов и слов «в лицо», таким образом, оно было направлено на оптимизацию и аналитического (чтение слогов), и целостного (глобального) чтения. Приведем в качестве образца две из восьми строчек одной из таблиц.

Примененные приемы позволили мальчику догнать упущенное и овладеть программой 3-го класса. Тем не менее определенные пространственные трудности у него сохранились. Так, итоговую контрольную за третью четверть по математике Егор сделал безошибочно, но, боясь совершить ошибку, он на всякий случай у учителя спросил, показывая на пример с вычитанием: «Из этого числа это вычитать?»

1. Лурия А. Р. Высшие корковые функции человека. – М., 1969.

2. Лурия А. Р. Очерки психофизиологии письма. – М., 1950.