Лекция 5

В начале мне хочется коротко обсудить характер взаимоотношений между говорящим и слушателями на подобных встречах. Они отличаются от того, что происходит на академических лекциях. Они похожи скорее на отношения дирижера и оркестра: способности слушателей ограничивают или расширяют власть говорящего. Нам очень повезло. У меня никогда прежде не было слушателей, среди которых так много музыкантов (это образное сравнение). Некоторые из вас – настоящие виртуозы, как явные, так и скрытые. Это наша совместная работа. Я хочу, чтобы сегодня, чуть позже, мы вышли в открытое море. До сих пор мы оставались у берега, едва замочили ноги, но сегодня я предлагаю нырнуть в глубину.

Перед этим я хотел бы представить вам одну концепцию, которую я разработал несколько лет назад, прочитав книгу философа Нортропа под названием «Встреча Востока и Запада» [1]. Он изложил там свои представления о характере восточного сознания – прежде всего, дальневосточного, но его рассуждения во многом справедливы и в отношении всего Востока. Он говорит о том, что обычное сознание представляет собой дифференцируемое эстетическое непрерывное пространство. Понятие «эстетический» не означает у него только красоту. Скорее, оно похоже на те соображения, которыми руководствовались при использовании этого термина Баумгартен [2] или Иммануил Кант, то есть означает упорядоченность чувственного сознания. Эта эстетичность представлена в плоском, двумерном искусстве Дальнего Востока. Помимо того, она проявляется в том, что мы называем номиналистической, фено-меналистической и позитивистской формой, которая так часто повторяется в буддийских сутрах и в направлении буддийской философии, именуемом философией Пустоты, или Шуньи. В ней видоизменения ощущаемого мира можно уподобить образам на поверхности мыльного пузыря; йога превращается в процесс ориентации в неопределимом эстетическом непрерывном пространстве – самом мыльном пузыре, который рассматривается отдельно от возникающих на его поверхности образов. Сначала сознание сталкивается с игрой образов, но путем Осознания рано или поздно начинает постигать то, что является не образом, а его основой.

Нортроп выделяет противоположный, западный гений, который развивается в измерении теоретического непрерывного пространства – в данном случае дифференцированного. Дифференцированное теоретическое непрерывное пространство является основой нашей науки. Примечательно, что математика Востока не идет ни в какое сравнение с ее развитием на Западе. Разумеется, мы заимствовали у Востока несколько важных принципов; в частности, из Индии к нам пришло понятие нуля -нечто чрезвычайно важное, хотя оно обозначает ничто. Знаменательно – и этого следовало ожидать, – что подобное понятие родилось у метафизического народа. И все же широкое развитие математической мысли в целом, которое стало основой всей западной науки, является заслугой гения Запада.

В качестве своего дополнения к этой мысли я предлагаю концепцию неопределенного теоретического непрерывного пространства как пути йоги – и это не перенос йоги на западную почву, а та форма йоги, которая исконно присуща человеку Запада. По моим представлениям, основная идея этой йоги была заложена Пифагором, так как его основной вклад в математику, возможно, стал и самым важным из когда-либо сделанных математических открытий – я говорю о принципе умозрительного доказательства. До него математические теоремы и утверждения опирались в основном на эмпирические доказательства. Из этого родилась монументальная структура, призвавшая к жизни невероятно могучую способность постижения. Я надеюсь, что сегодня вечером смогу немного познакомить вас с ней. Многие среди вас не имеют достаточной специальной подготовки. Вам будет трудновато, но, если вы почувствуете, что почва уходит из-под ног, просто откиньтесь на спинку стула и отдохните.

У меня есть своя причина, чтобы познакомить вас с этими вещами. Она связана с одним абзацем в книге «Пути в иные измерения» – началом раздела 52 «Высокая Беспристрастность». Мне известен только один человек, который прочел этот абзац и уловил заключенную в нем важнейшую аналогию.

Как описать то, что случилось со мной прошлой ночью? Все, что я могу об этом сказать, в лучшем случае будет лишь намеком на Нечто, ибо это не было ни внутренним событием, ни интеллектуальным проникновением; как познавательная способность, так и возможности восприятия – безнадежно, абсолютно неадекватны на этом Уровне. Как бесконечное для конечного, таким же было и это Сознание для относительного сознания субъектно-объектной множественности. Я проник в Состояние не только полностью вне сферы относительного, но и вне всего, что Постиг прежде. Поистине, в Бесконечности -тайна за тайной, глубина за глубиной, величие за величием. И как в математике есть бесконечности высшего порядка, бесконечно превосходящие бесконечности низшего порядка, – так и в Трансцендентном Мире. Значит, нет конца возможному Пробуждению? Нет конца прогрессии бесконечностей? Может быть. Я знаю только, что нашел некий бесконечный Мир, а затем другую Бесконечность, поглотившую этот Мир. Я могу лишь свидетельствовать, что эти Миры существуют, но я не в силах наложить никаких ограничений на Высшее. Тайна Тайн, простирающаяся внутрь и вовне, но всегда Запредельная! И из этой Безмерности идут все новые отзвуки иной, неощутимой Красоты! Как же мал этот мир в начале Тропы… [3]

Тот человек распознал здесь аналогию с канторовской бесконечностью. Он был опытным физиком-теоретиком, преподавателем горного дела в Колумбийском университете, автором учебников по термодинамике. Но у него возникла тяга к мистическому. Он уже не мог продолжать свою работу. Он был вынужден оставить место, хотя ему предлагали повышение и даже годичный контракт на преподавание в Принстонской высшей школе. Он все равно не мог продолжать. В конце концов ему в руки попалась моя книга, и, судя по его письмам, только этот человек понял, о чем я говорил: приведенный абзац – не поэтическое преувеличение, это полное и буквальное описание.

Итак, у нас есть два способа осознания. Они известны нам по сфере обычных переживаний – в данном случае научного познания. Я расскажу вам историю открытия Нептуна. Исходя из возмущений в движении ближайшей к нему внешней планеты Уран, некоторые математики Англии и Франции высчитали, что в определенной точке пространства должна находиться планета с предполагаемыми характеристиками. Один из английских ученых [4] связался с астрономом Гринвичской обсерватории и попросил его навести телескоп на эту точку в расчете на открытие новой планеты. Во Франции то же самое сделал другой ученый [5], но его просьбу презрительно отвергли, и в результате планету первым увидел английский астроном. Этот случай иллюстрирует два способа познания – математический и чувственный. Сначала состоялось открытие путем выявления новых математических взаимоотношений и расчетов, а затем последовало открытие посредством зрительного наблюдения. В относительном сознании эти два способа являются взаимодополняющими.

В йоге используется такой же принцип. Существуют несколько философий йоги, одна из которых, самая важная, была развита Шри Шанкарачарьей [6]. Человек может изучить философию и удостовериться в ее обоснованности, логической последовательности. Он может полностью принять такую философию. Это не Осознание. С другой стороны, если Дверь распахивается, человек постигает Невыразимую Действительность, основополагающее quale [7] которой просто невозможно передать словами.

Поскольку мне знаком этот путь, я могу говорить о нем. Кое-что из Внутреннего можно объяснить. Логика Шанкары меня полностью убедила. Конкретным методом был майявадин, то есть взгляд на все проявленное, на окружающий мир как на иллюзию, не имеющую ничего общего с Истиной. Это стало итогом исканий, длившихся двадцать четыре года – за это время я бесповоротно пожертвовал своей академической карьерой. По завершении этих двадцати четырех лет я постиг только одно: нет ничего такого, к чему следовало бы стремиться. Логичносгь этого вывода очень легко понять. Если или все прочие создания представляют собой ТО – по самой природе Предельной Действительности, пусть даже она скрывается за покровом внешнего сознания, – то я просто не в состоянии достичь такой Предельной Действительности: ведь я, как и все остальные создания, уже есть ТО. Эта йога была связана с Я, с поисками Себя – не эго, а именно Себя. Эти два понятия сильно различаются. Эго может служить объектом сознания, а Я – нет. Если вы попытаетесь сосредоточиться на нем, то окажетесь в круге бесконечных повторений. Если вы решите, что способны наблюдать его, то вновь и вновь будете задавать себе вопрос: «Кто же наблюдает?» Я наблюдаю. Всякая попытка поместить его в сферу наблюдения станет очередным шагом назад – до тех пор, пока вы не научитесь вообще не рассматривать его сознанием и просто погружаться в него.

Однажды я читал об Освобождении в духе Шанкары в книге Дейссена «Системы веданты» [8] и понял эту мысль совершенно отчетливо: нет ничего такого, чего следует или можно достичь. В тот миг я отбросил все свои стремления и с тех пор не пытаюсь ничего добиться -потому что я уже есть ТО, чего ищу.

Я решил, что после этого уже ничто не может случиться, но на самом деле я только распахнул все заслонки. Произошло вознесение сознания. Это очень приблизительное выражение, но именно так оно ощущается. Все это явление относится к той сфере, которую я бы назвал метапсихологией. Я оказался выше пространства, времени и закона, то есть стал совершенно свободным. Логику происшедшего вновь нетрудно понять: ТО, которое является источником пространства, времени и закономерности, по необходимости пребывает вне обусловленности пространством, временем и законами. Индийцы называют это словом Парабрахман, а буддисты, возможно, назвали бы алайявиджняной [9]. Основополагающий принцип философии Шанкары заключается в том, что любое создание рассматривается как тождественное Парабрахману. Обратите на это внимание: тождественное не какой-то его части, а всей целостности Парабрахмана. Таким образом, последователь йоги должен мыслить самого себя частью и частицей всего целого, а не отдельной его деталью.

В подобные мгновения разум обычно спотыкается и не желает двигаться дальше; но, благодаря достижениям в области математики, у нас есть достаточно понятные символы, вмещающие такое содержание – и позволяющие его передать. За это следует благодарить, в частности, Дедекинда [10].

Я предлагаю вам взглянуть на самую обычную систему чисел: 1, 2, 3, 4, 5 и так далее, без конца. Одновременно рассмотрим ряд тех же чисел, умноженных на 2:

1 2x1=2

2 2x2=4

3 2x3=6

4 2x4=8

5 2x5 = 10

n 2хn = 2n

Два таких ряда обладают взаимно однозначным соответствием: это простейший процесс нумерации членов ряда. Можно заметить и другое свойство: каждое число из второго ряда обязательно встретится в первом, однако второй ряд не включает в себя всех членов первого ряда. В нем нет нечетных чисел, однако тот факт, что мы установили взаимно однозначное соответствие, позволяет утверждать, что эти ряды одинаковы. Они просто расширяют обычный порядковый счет.

Представим себе пастуха, который пересчитывает своих овец – скажем, по пальцам. Он устанавливает обычное взаимно однозначное соответствие; если пальцев на руках и ногах не хватает, он может воспользоваться камешками. Он подсчитывает овец, откладывая камни в сторону (например, в мешочек), и, вернувшись домой, объявляет: «У меня столько-то овец». Так было до тех пор, пока не возникли абстрактные числа. Таким был первоначальный счет. Камешек называли «calculus», и позже это слово стало основой для понятий «калькуляция», то есть «подсчет, вычисление, исчисление». Впрочем, для врача слово «calculus» означает совсем другое*, но это не важно. В действительности при таком подсчете мы просто устанавливаем взаимно однозначное соответствие между двумя рядами: набором камешков и отарой овец. В нашем случае мы проделали то же самое с двумя числовыми рядами, а когда количество камней и овец сходится, мы говорим, что эти множества равны по своей мощности, то есть по количеству элементов. В данном примере мы столкнулись с равенством, с тождественностью двух рядов – ряда целых и ряда четных чисел; соответствие между этими рядами продолжается до бесконечности: каким бы большим ни было число в первом наборе, во втором всегда найдется число в два раза больше. Теперь представим себе, что второй ряд является некоей сущностью, которая выглядит отделенной от своего основного источника, первого ряда. Его объединение с основным источником станет слиянием со всей целостностью источника в его полной протяженности. Поскольку мы можем построить бесконечное множество рядов вида З* (число), 4* (число),… n* (число) – или, например, степенных рядов (число) в степени 1, (число) в степени 2, (число) в степени 3 и так далее до (число) в степени n, – то, следовательно, способны получить бесчисленное количество подмножеств или, если угодно, вычетов из исходного многообразия. Пусть первоначальная последовательность целых чисел олицетворяет Парабрахмана, а каждый порожденный на ее основе ряд – того же Парабрахмана, который забыл самого себя. Он возвращается к Отождествлению с целостностью первоисточника, так как каждая грань его существования соответствует некоторой частице целостности. Эта аналогия подразумевает, что целостность сущности каждого из нас, Подлинной Сущности, не конечна, а беспредельна. Это – часть логики бесконечности, представленная в математических понятиях.

Вернемся к тому переживанию или, точнее, Осознанию (я избегаю слова «переживание», так как хочу ограничить его применение более узкой областью, а именно сферой чувственного восприятия; понятием «Осознание» я называю иной способ постижения, отличный от чувственного и умозрительного). Я говорил об ощущении Освобожденности. При этом возникает свойство Восторга, превосходящее все то, что доступно воображению относительного сознания. Я повторил бы то, что один за другим говорили мистики: это Сокровище, это Счастье в буквальном смысле дороже любых жертв. Даже страдания на протяжении всей жизни могут оказаться недостаточно высокой ценой. Это невозможно вообразить. Восторг – не удовольствие, а Блаженство. Это ощущение высшей Чистоты, Радость, очищающая намного лучше, чем страдания. Запомните: это совсем не эгоистическое наслаждение удовольствием. Аналогия с удовольствием вообще не уместна. Это выходит так далеко за пределы воображения, что трудно подбирать слова. Мистики часто пользуются выражениями, которые выглядят неправдоподобными преувеличениями, но фактически оказывается, что любой существующий язык лишь преуменьшает выразительность этого богатства. Это не эгоистическое переживание, а способность благословлять: с ней связано не только нравственное стремление благожелательности, но некое пространство Благости, окутывающее всякого, кто вошел. Благожелательность перестает быть вопросом нравственной дисциплины, она является частью ТОГО.

Я, можно сказать, совершал переходы туда и обратно между относительным сознанием и этим, более глубоким состоянием, и очевидным стало одно: в определенный момент случается некое смещение, которое можно инстинктивно назвать «переворотом сознания». Слово «переворот», «инверсия» часто встречается в трудах Ауробиндо. Не совсем ясно, что именно оно собой представляет и как можно подступиться к его анализу. В миг переворота возникает нечто имеющее определенное сходство с тем, что математик назвал бы «разрывом непрерывности»: одно сознание затуманивается и на его месте мгновенно возникает иное. Были случаи, когда я намеренно путешествовал туда и обратно, пытаясь сохранить непрерывность сознания, но это мне не удавалось. Разрыв все равно происходил – и очень быстро. С одной стороны (сейчас я высказываю точку зрения обычного сознания) оставалось: «Я – относительная личность, обусловленная тем, что окружает меня извне», а с другой возникало: «Я – ТО, поддерживающее вселенную». Было и ощущение того, что Я возносится и нисходит. Я никогда не встречал описаний чего-либо подобного в книгах; и я без особой уверенности использовал термин «восходящее Я». Быть может, это только видимость. Сейчас мне так не кажется – скорее, я думаю, оба типа сознания действуют параллельно. И все же был этот вид переживания я, пребывающего в сфере относительности, ограниченного, скованного, обусловленного окружающим миром-то есть высшим Я, поддерживающим целую вселенную. Только не воображайте себе Атласа, физически подпирающего что-то плечами. Это вселенная нашего сознания, единственная известная нам, – но, следует отметить, вселенная всего сознания, а не только относительного. Единственной подлинно важной вселенной является то мироздание, которое существует в нашем сознании, а Я служит ее основой, поддерживает ее. Однако это Я не является собственно личностью; подобно этому, солнце, отражающееся во множестве росинок, едино, а его множественность в каплях росы остается иллюзией. На самом деле, отражение солнца в росинке является неотъемлемой частью и частицей солнца в небе – точно то же самое можно сказать и про Я. Иными словами, Атман тождествен Параматману, и когда я говорю: «Я поддерживаю эту Вселенную», то эти слова представляют собой не безграничный эгоизм, не раздутую гордыню, а извечный факт, с которым сливается личное сознание: как только это слияние происходит, человек становится частью Всеобщего Сознания.

Я называю это состояние «Нирвана» [11]. Я не знаю, так ли понимают его другие. В то время оно казалось моему рассудку окончательным состоянием, самым желанным из всех возможных. В моих представлениях Нирвана, или Мокша [12], располагалась вертикально по отношению к миру видимых форм, Сансаре, но при этом Нирвана была Абсолютной, а Сансара – относительной.

Итак, я размышлял на протяжении тридцати трех дней. Меня предупредили, чтобы я был внимателен к циклу тридцать три. Разумеется, я мыслил о тридцати трех годах, тридцати трех жизнях, месяцах и тому подобное, но не подозревал, что речь может идти всего о тридцати трех днях. Я не знал, что есть что-то еще, и по этой причине не искал ничего иного – и в результате перешел к такому сознанию, которое относилось к обычному так, как я только что описал: как Бесконечность более высокого порядка. Теперь мне придется воспользоваться символикой теории бесконечных чисел, которую разработал Кантор [13].

Прежде всего, давайте, насколько сумеем, подойдем к этой теме с точки зрения представительного описания, которое может быть названо «метапсихологией». Если говорить об ощущениях, то лейтмотивом самых первых переживаний было состояние невообразимого Восторга. Не думайте, что этот Восторг не является Силой. Физическому организму очень трудно переносить это Состояние. В самом Состоянии нет ничего сложного, но когда человек весь открывается ему, оно может истощить даже крепкий физический организм. Оно вызывает в теле чувство усталости, и одним из следствий может оказаться достаточно сильное отвращение к физическому организму. Его хочется сбросить. Такое искушение возникает совсем не редко.

Если вы хотите определить состояние сознания, то их – два. Возникает противопоставление: Восторг – и этот, низший мир, царство страданий. Это означает, что здесь даже удовольствие или наслаждение, если вы их испытываете, могут приводить к боли. То, что мы называем весельем, есть страдание – так проявляется целостность. Таким образом, лейтмотивом низшего мира является страдание, Сансара. Имеем дуализм: вверху – Восторг, внизу – боль. В таких условиях возникает побуждение к выбору, к предпочтению. Кем бы ни были мы, люди, наше состояние нельзя назвать совершенно не двойственным состоянием, оно не обладает полным равновесием.

Тридцать три дня спустя, в ночь с 8 на 9 сентября 1936 года произошло важное событие: я перешел к состоянию совершенной уравновешенности, в котором сознание с равным отношением взирало и на Высший Восторг, и на страдание. Обычное человеческое сознание вряд ли пожелает оказаться в таком положении, но это Осознание превосходит то состояние, которое было Осознано прежде, подобно тому как бесконечность высшего порядка превосходит бесконечность меньшей мощности. Я мог бы сказать, что это Сознание вообще не является человеческим – во всяком случае, в обычном смысле этого слова, поскольку любое человеческое сознание обусловлено предпочтениями. Это Сознание было свободно от каких-либо склонностей и представляло собой состояние совершенного эмоционального равновесия. Если бы возникли причины погрузиться в мир страданий, то с точки зрения этого Сознания такой переход оказался бы столь же легким, как и погружение в царство Невыразимого Восторга. Я понимаю, что это трудно вообразить, но говорю, опираясь на собственный опыт. Там нет никаких предпочтений. Господствует глубокое Осознание того, что нет такого существа, которое испытывало бы страдание, что ни единая частичка целого никогда не оказывалась потерянной. Там все пребывает вечно. Единственное происшествие в этом мире можно описать так: Изначальный Источник всего сущего на мгновение сомкнул глаза, и в течение этого мига привиделось, будто протекли миллиарды [14] лет, в это время вселенная якобы развивалась, существа как будто бы рождались и испытывали страдания – но вот глаза открылись, этот мир исчез, и все опять здесь. По этой причине теряет свою силу памятное обязательство Освобождения или Просветления всех созданий, поскольку нет такого создания, которое уже не являлось бы Просветленным. Нет ни одного страдающего существа – есть только мимолетная дремота, в которой возникает воображаемый образ Вселенной, растянутый на миллиарды лет. В этом состоянии не возникает побуждений к каким-либо действиям, но любое принятое решение стало бы Божественно правильным. Остаться, задержаться в этом Состоянии во всей его полноте либо вернуться в сферу кажущегося развития – Божественно правильным окажется любое из этих решений. Это полная свобода выбора, хотя нет никаких причин, подталкивающих к тому или иному выбору. Нет ничего такого, что выделяло бы один или другой путь, нет ничего лучшего или худшего – только Совершенное Равновесие. Любое решение становится произвольным, не имеющим никаких причин.

На следующее утро я вновь оказался в этом мире, в сознании этого мира. Судя по всему, решение все же было принято, но, при всей произвольности, оно было ничуть не лучше любого другого возможного решения. Так я узнал нечто новое, чего не встречал ни в сутрах, ни в шастрах, несмотря на то что читал их очень внимательно. Едва ли я мог найти нечто такое, что предоставило бы хотя бы слабый намек на это. Кое-что в моих взглядах решительно изменилось: я стал совершенно иначе смотреть на характер отношений между Нирваной и Сансарой, деятельной вселенной. Я понял, что Нирвана не абсолютна, а относительна, что даже в ней сохраняется двойственность; а Высшее Сознание, в котором я побывал, есть, помимо прочего, слияние этой двойственности. Таким образом, Нирвана относительна. Позже, обратившись к некоторым сутрам тибетского буддизма под редакцией Эванса-Вентца [15], я встретил там эту мысль: Нирвана во вселенной действия относительна, и если человек превосходит такую Нирвану, то она может перейти в нефиксированную Нирвану. Если человек входит в нирваническое состояние по первому способу, он оказывается запертым – точно так же, как прежде был заперт в состоянии Сансары. Он не может покинуть его по желанию; а нефиксированная Нирвана позволяет переходить в нее и покидать ее по собственной воле. Таким образом, это стало определенным подтверждением, и все же в моем переживании были и другие особенности, намеков на которые я не встречал в книгах.

Я уделил много времени описанию этого состояния сознания, а теперь намерен предложить вам метод интеллектуального постижения его масштабов, опираясь на определенные понятия современной математики. Эта умственная разминка потребует определенной гибкости ума. Мы пользуемся понятием «бесконечность» довольно легкомысленно. Говорят, готтентоты умеют считать только до трех. Для них бесконечно все, что больше числа три. Один поэт говорил о бесконечности ночного неба, подразумевая при этом видимые звезды – однако их лишь чуть больше трех тысяч. Он, видимо, смог досчитать до трех тысяч, а все, что сверх этого, оказалось для него бесконечностью. Истинная бесконечность – нечто иное. Рассмотрим число 1+Е100 – единицу с сотней нулей; это число называется «гугол». Оно намного превышает наш национальный долг, составляющий всего 300 000 000 000 долларов [16]. В последнем числе только двенадцать цифр. Добавим к нему еще один нуль и получим число в десять раз большее; добавим два – и оно станет в сто раз больше, три – в тысячу раз.

Исходный долг составляет всего одну десятую процента (0,1%) от третьего числа, но и в этом, последнем числе только пятнадцать цифр, а у гугола сто нулей. Выходит, полученное нами число по-прежнему очень мало по сравнению с гуголом. Вероятнее всего, гугола, или десяти в сотой степени, вполне хватит для того, чтобы сосчитать все капли дождя, упавшие на Землю за весь геологический период.

Обратимся к другому числу, по сравнению с которым даже гугол покажется совсем крошечным. Это число можно было бы назвать «гуголлион». Записывается оно как десять в степени гугол:

₁₀гугол

или, иначе, как десять в степени десять в сотой степени:

10^{10^100 .}

Чтобы записать это число в полном виде, потребуется добавить к единице гугол нулей. Постичь это способен далеко не каждый. Однажды я объяснял эту мысль одному врачу, и тот никак не мог уловить ее, пока я не сказал, что есть огромная разница между записью миллиона как единицы с девятью нулями и записью числа с миллионом нулей после единицы. После этого он сразу понял смысл.

Чтобы вызвать у вас представление о подобной беспредельности, я попрошу задуматься о том, сколько места потребуется для записи «гуголлиона», то есть строки из гугола нулей. Когда-то я уже обращался с таким вопросом к группе слушателей. Предположим, у нас есть бумажная полоска, и каждый нуль представляет собой кружок диаметром в четверть дюйма. Какую длину будет иметь такая полоска?

Один человек предположил, что ее хватит, чтобы обернуть земной шар по экватору. Другой, более реалистичный, сказал: «Скорее всего, миллион световых лет». Световой год представляет собой то расстояние, которое проходит за один год луч света, движущийся со скоростью 186 тысяч миль в секунду. Однако и эта догадка оказалась сильным преуменьшением. Представьте себе конечную вселенную (какой она является в соответствии с принципами Эйнштейна), поперечник которой составляет три миллиарда световых лет [17]. Вообразите это: огромная сфера диаметром в три миллиарда световых лет. Теперь представьте наши нули как крошечные сферы размерами меньше атома, но чуть больше его ядра. Заполните этими маленькими шариками весь объем сферы вселенной, и тогда у вас как раз хватит нулей, чтобы записать число «гуголлион». Я проверил это расчетами, а позже встретился с подсчетом количества электронов, необходимых для того, чтобы до отказа наполнить ими всю вселенную. Полученная оценка составляла десять в сто десятой степени (10¹¹⁰). Это, конечно, больше, но не намного – всего на несколько порядков, то есть наш расчет не так уж плох*.

Однако и «гуголлион» становится крошечным, когда речь заходит о Бесконечности. Работая с бесконечными числами, математики имеют дело с превосходящей любое воображение беспредельностью. Я имею в виду, что бесконечность как понятие аналогична Осознанию как факту; это помогает оценить ее значимость.

Особый вклад в эту область внесли два человека: Дедекинд и Кантор. Дедекинд первым ввел представление о бесконечности как о многообразии, или множестве, такого характера, что в нем есть определенная часть, содержащая столько же элементов, сколько их содержит все целое, – подобный пример мы рассматривали немного раньше. Когда Дедекинд перешел к формулировке своей теоремы о существовании в рамках этики, то, ставя вопрос о том, существует ли такая бесконечность, он взял в качестве примера человеческое мышление. В разуме возникает некая мысль, а затем может появиться мысль об этой мысли, потом третья мысль о второй и так далее; возникает последовательность:

1 Мысль 1

2 Мысль 2

3 Мысль 3

n Мысль N

Во втором ряду столько же элементов, сколько их в первом. Кроме того, существует один элемент – то самое Я, – который не входит в последовательность мыслей. Таким образом, один ряд является однозначно соответствующей частью другого, то есть равен его полноте. Это значит, что человеческий разум потенциально бесконечен – не только в психологическом, но и в более глубоком смысле.

Сейчас мне хочется познакомить вас с математической индукцией – и не только для того, чтобы узнать новый математический факт. Это позволит нам лучше понять сам разум, так как индукция демонстрирует принцип выявления истины, чрезвычайно важный для всей математики и ее отношения к истине. Одновременно мы сравним этот принцип с законами обычной формальной логики. Пусть, например, этот круг включает в себя все смертные существа (см. рис. 20).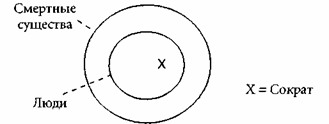

Рис. 20

Все люди смертны. Это равносильно утверждению о том, что люди (множество которых мы изобразим кругом меньшего диаметра) образуют некое подмножество класса смертных существ. Далее можно сказать, что Сократ (отдельный элемент, обозначенный символом «X») – человек. Поскольку он входит в меньший круг, можно прийти к выводу о том, что Сократ смертен. Таков схематический способ изображения этого силлогизма [18]. В данном случае мы воспользовались дедуктивной логикой: спустились из обширной области в более узкую методом исключения. Такая форма логики является не очень творческой, она больше пригодна для целей критического рассмотрения, анализа и так далее.

В индуктивной логике – в том привычном смысле, в каком она применяется в науке, – законы выводятся исходя из ряда наблюдений. Например, увидев набор точек на плоскости, вы можете попытаться придумать некую гипотезу, которая объяснит закономерность или взаимосвязь между положениями этих точек. В одной лекции я говорил о примере поиска подобной закономерности в расположении пяти точек. Если вы наложите на этот закон ограничение и потребуете, чтобы он представлял собой уравнение второй степени, то найдете единственное решение, поскольку пять точек на плоскости однозначно определяют кривую второй степени. Но если вы не будете сковывать свое мышление такими ограничениями (то есть допустите, что закон может быть уравнением третьей, четвертой, пятой и любой другой степени), то через эти пять точек может пройти в буквальном смысле слова бесконечное число кривых.

Иначе говоря, существует бессчетное, потенциально бесконечное число возможных объяснений наших научных наблюдений – потенциально неисчислимое разнообразие. Мы не можем добиться однозначной, определенной истины. Именно по этой причине аксиоматическая наука имеет только прагматическую ценность. Она некоторое время помогает, но рано или поздно становится неверной. После обобщения Ньютона люди считали, что наконец-то постигли истину. Эта точка зрения сохранялась очень долго, но и она была опровергнута. Теории Ньютона не удалось объяснить некоторые измерения после того, как люди смогли провести их точнее. Сегодня более адекватными считаются идеи Эйнштейна, но завтра и они могут смениться новыми представлениями. Таким образом, аксиоматическая наука предлагает не окончательную, а прагматическую истину.

Математическая индукция представляет собой тот процесс, благодаря которому мы можем переходить от чего-то конкретного и единичного к бесконечности в буквальном смысле. Я попытаюсь показать вам простой пример. Рассмотрим сумму:

1 + 3 + 5 + 7+…

и так далее, без конца. Этот ряд представляет собой сумму нечетных чисел. Для обозначения номеров каждой промежуточной суммы этого ряда я буду использовать римские цифры – они отличаются от привычных и потребуются нам для поиска окончательной формулы.

Количество слагаемых: I II III IV… n n+1

Слагаемые: 1+ 3+ 5+ 7+…+ (n-1) + (2n+1) +…

Сумма слагаемых: 1 4 9 16… n² (n+1)²

Обратите внимание, что первая сумма равна 1, сумма первого и второго членов-4, сумма первых трех слагаемых – 9, сумма первых четырех – 16. Заметили ли вы зависимость между этими суммами и теми числами, которые обозначают количество слагаемых? Во всех случаях суммы равны квадратам этих чисел – довольно неожиданный результат! Теперь вас осеняет мысль: быть может, такое правило выполняется на всем протяжении этого бесконечного ряда. Для того чтобы проверить все суммы, потребуется бесконечное время. Однако математик не скован таким требованием.

Смотрите, как он поступает. Сначала он допускает, что это правило выполняется для n слагаемых (при этом п означает любое целое положительное число), то есть сумма первых n членов ряда равна n² – такое предположение возникло в результате того, что ему уже известно. Затем он задает себе • вопрос: «Будет ли это выполняться и далее?» Будет ли это утверждение справедливо для суммы (п+1) первых слагаемых, если известно, что оно выполняется для суммы n слагаемых? Получим ли мы (n+1)² в результате очередного суммирования? Математик поступает просто: берет сумму п первых членов и говорит, что она равна n². В каком виде можно представить n-ый член этого ряда? Заметим, что ряд можно записать в форме:

2*(1)-1, 2*(2)-1, 2*(3)-1, 2*(4)-1,…

и тогда n-ое по счету слагаемое будет иметь вид 2n – 1. Определим (n+1)-ое слагаемое, заменив n на (n+1). Получим:

2(n+1)- 1 = 2n+ 1.

Это легко проверить, так как нам известно, что каждое слагаемое ровно на 2 больше предшествующего слагаемого. Сложим это слагаемое с полученной ранее суммой n² и посмотрим, будет ли новая сумма равна (n+1):

n²+(2n+1) = n²+2n+ 1

Те, кто помнит школьную математику, уже узнали эту формулу: записанное справа выражение равно

(n+1)².

Иными словами, если сумма первых n членов ряда равна n², то сумма первых (n+1) членов будет равна (n+1)².

Таким образом, если это правило выполняется для какого-либо члена ряда, то оно будет справедливо и для следующего члена. Правильность закономерности для нескольких первых сумм была показана практическим методом, то есть прямыми вычислениями, но теперь нам ясно, что она сохранится на всей бесконечной протяженности этой последовательности. Такой подход постоянно используется в математических доказательствах.

Какое отношение это имеет к нашему разуму? Только что мы убедились, что несколько первых слагаемых позволяют нам с полной уверенностью судить о том, что произойдет с сотым, тысячным слагаемым, со слагаемым под номером гугол – с любым из всей бесконечности слагаемых. Эти факты известны нам с неоспоримой точностью. И это показывает, что разум не является чем-то конечным. Мне хотелось дать вам представление именно об этом, и не с точки зрения Осознания, а под неким иным углом, с позиции мышления, умозрительного понимания. У нас есть основания считать, что подлинный разум не есть что-то ограниченное, что это не просто заключенный в череп мозг, а нечто такое, что в определенном направлении простирается безгранично. Математик пользуется этой силой, чтобы строить свои доказательства. Благодаря приведенным выше рассуждениям он определяет, чему будет равна сумма произвольного количества слагаемых, с той же уверенностью, с какой складывает первые несколько членов этого ряда. Это отчасти приоткрывает тайну подлинного разума: в действительности, мы вовсе не ограниченные создания, мы так же велики, как Парабрахман. Я уже говорил о том, что, вполне возможно, существуют еще более глубокие Источники, чем те, которые представлены в идее Парабрахмана. Некоторые люди поднялись на огромные высоты и принесли нам эту идею, но что запрещает нам со временем подняться еще выше и проникнуть, как говорит Ауробиндо, в неведомые, беспредельные Бесконечности?