Ну вот мы и добрались до самого главного. Основная задача логики – анализ рассуждений, а рассуждения складываются из предложений и слов или, говоря иначе, из суждений и понятий. Поэтому знакомство с логикой мы и начали с рассмотрения тех простых элементов, из которых образуются сложные мыслительные конструкции. Теперь можно познакомиться с самими этими конструкциями.

Умозаключение есть форма мышления, в которой из одного или нескольких суждений на основании определенных правил получают новое суждение.

Наши рассуждения в повседневной жизни или в профессиональной сфере – это и есть умозаключения или цепи умозаключений. Умозаключение есть средство извлечения нового знания из уже имеющегося. То знание, которое мы получаем в результате непосредственного контакта с окружающей средой, очень невелико – оно ненамного превосходит знания животных. Но на этом небольшом фундаменте человек воздвиг колоссальное сооружение, включающее в себя знание о звездах и галактиках, о структуре атома и элементарных частицах, о законах, управляющих наследственностью, о древних цивилизациях, об исчезнувших языках и океанских глубинах. Все это знание получено благодаря умению человека строить умозаключения.

Иногда человеческий ум определяют как способность строить умозаключения, делать выводы. Может быть, ум состоит не только в этом, но, несомненно, способность строить умозаключения и извлекать выводы из имеющейся информации – одна из важнейших его сторон. Вы смотрите утром на градусник, висящий за окном, и видите, что ртуть в нем опустилась до –70°C. Вот все, что у вас есть. Но отсюда вы делаете вывод, что на улице мороз. Вы еще не были на улице, не ощутили своей кожей укусов ветра, но уже знаете – там холодно. Откуда у вас это знание? Его вам дало умозаключение. Вы можете сделать еще один вывод: выходя на улицу, нужно одеться потеплее. Вы предвидите, какое воздействие окажет на вас мороз. Предвидение – это тоже умозаключение. Умный человек – тот, кто способен извлечь из имеющегося знания максимум новой информации, предвидеть ход событий и последствия своих действий. Шерлок Холмс и его друг доктор Ватсон часто ходят вместе, видят и слышат одно и то же, однако Холмс умеет извлечь из этого гораздо больше, чем Ватсон, поэтому и кажется нам умнее и проницательнее своего друга.

Всякое умозаключение состоит из двух частей: те суждения, из которых мы исходим, на которые мы опираемся в умозаключении, называются его посылками, новое суждение, извлекаемое нами из посылок, называется выводом. Все умозаключения разделяются на две большие группы – дедуктивные и индуктивные.

Дедуктивными называют такие умозаключения, в которых вывод из посылок следует с необходимостью, т.е. если посылки умозаключения истинны, то вывод обязательно будет истинным. Например, если мы знаем, что все гасконцы являются французами и д'Артаньян является гасконцем, то отсюда мы можем сделать вывод о том, что д'Артаньян является французом. И этот вывод будет безусловно истинным.

Об индуктивных умозаключениях мы позднее поговорим особо (в разделе «Индукция»), а сейчас познакомимся с некоторыми простыми и наиболее употребительными дедуктивными умозаключениями. Мы интуитивно используем их в повседневных рассуждениях, но часто ошибаемся, ибо не отдаем себе отчета в том, что это такое.

1) Вдоль стен квадратного бастиона комендант разместил 16 часовых, по 5 человек с каждой стороны, так, как показано на рисунке: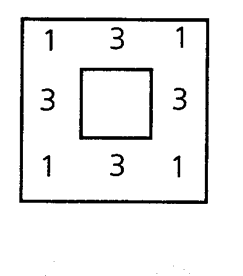

Через некоторое время пришел полковник, выразил недовольство расстановкой часовых и переставил их так, что с каждой стороны оказалось по 6 человек. Однако после этого появился генерал. Он также выразил недовольство и переставил часовых таким образом, что с каждой стороны их оказалось по 7.

Как расположил часовых полковник? Как их расставил генерал? Общее число часовых остается одним и тем же.

Непосредственными называют умозаключения из одной посылки, представляющей собой простое суждение.

Превращение состоит в том, что мы в нашу посылку вставляем два отрицания – одно перед связкой, а другое – перед предикатом, и так получаем новое суждение. Умозаключения принято изображать так: сначала пишется посылка (или посылки), под ней проводится черта, обозначающая слово «следовательно», а под чертой пишется вывод. Пусть посылкой у нас будет общеутвердительное суждение, тогда превращение выглядит так:

Все S есть P

Ни одно S не есть не-P

Например, суждение «Все металлы электропроводны» превращается в суждение «Ни один металл не является неэлектропроводным».

Если в качестве посылки взять общеотрицательное суждение, то превращение будет выглядеть так:

Ни одно S не есть P

Bce S есть не-P

Например, суждение «Ни один мошенник не является честным человеком» превращается в суждение «Все мошенники являются нечестными людьми». Когда здесь мы вставляем «не» перед связкой, то перед ней получаются два «не». Мы устраняем их, опираясь на принцип: двойное отрицание эквивалентно утверждению.

Конечно, вывод в таких умозаключениях дает очень мало нового по сравнению с посылкой. Это вполне естественно, так как мы по сути дела одному и тому же суждению лишь придаем иную языковую форму. Это не столько логическая, сколько грамматическая игра. Однако преобразование такого рода способно сделать явными некоторые оттенки смысла первоначального суждения, которые были скрыты в исходной формулировке. Мы часто пользуемся превращением суждений в повседневной жизни, когда хотим более ясно и отчетливо выразить свою мысль. Это часть нашей языковой способности.

Еще одной разновидностью непосредственного умозаключения является обращение. При обращении вывод получается путем постановки предиката посылки на место субъекта, а субъекта посылки – на место предиката. Общая схема обращения выглядит следующим образом:

S есть P

P есть S

Например, из суждения «Птицы есть позвоночные» мы путем обращения получаем вывод «Позвоночные есть птицы». Для того чтобы реально осуществить обращение, мы должны не просто поменять местами субъект и предикат, а сделать объект, отображаемый предикатом посылки, предметом нашей мысли, т.е. превратить его в субъект нового суждения. Иногда, например, производят обращение так: из суждения «Все рыбы дышат жабрами» получают вывод «Дышат жабрами все рыбы». Здесь нет логической операции обращения! Мы просто поменяли местами подлежащее и сказуемое. Чтобы получить обращение первоначального суждения, мы должны сделать предметом нашей мысли «дышащих жабрами» и говорить о них: «Дышащие жабрами есть рыбы».

В посылке перед субъектом стоит слово (квантор): «все» или «некоторые». Возникает вопрос: что мы должны поставить перед предикатом посылки, когда делаем его субъектом вывода, – «все» или «некоторые»? «Все дышащие жабрами» или только «некоторые дышащие жабрами» есть рыбы? Пытаясь ответить на этот вопрос, мы начинаем вдумываться в содержание понятия «дышащие жабрами», вспоминаем, а кто еще, помимо рыб, мог бы дышать жабрами, быть может, лягушки или какие-нибудь тритоны? Не нужно всего этого! Логика – наука формальная и вовсе не обязана знать, чем занимаются лягушки или рыбы, как математика, складывая 2 и 3, вовсе не интересуется тем, что вы считаете – рубли, доллары или кирпичи. Логика задает формальные правила, не зависящие от содержания наших понятий и суждений. В данном случае правило таково: если посылкой является утвердительное суждение, то при обращении перед предикатом ставят слово «некоторые»; если же посылка является отрицательным суждением, то перед предикатом ставят слово «все». Наша посылка «Все рыбы дышат жабрами» является утвердительным суждением, значит, из нее можно сделать вывод «Некоторые дышащие жабрами есть рыбы». А вот из отрицательной посылки «Ни один слон не живет в Арктике» можно сделать общий вывод «Всякий живущий в Арктике не есть слон».

2) Три путешественника забрели на постоялый двор, хорошо покушали, заплатили хозяйке 30 руб. и пошли дальше. Через некоторое время после их ухода хозяйка обнаружила, что взяла с путешественников лишнее. Будучи женщиной честной, она оставила себе 25 руб., а 5 руб. дала мальчику, наказав ему догнать путешественников и отдать им эти деньги. Мальчик бегал быстро и скоро догнал путешественников. Как им разделить 5 руб. на троих? Каждый из них взял по 1 руб., а 2 руб. оставили мальчику в награду за быстроногость.

Таким образом, они заплатили за обед по 10руб., но по 1 руб. получили обратно, следовательно, они заплатили: 9х3 = 27руб. Да 2 руб. осталось у мальчика: 27 + 2 = 29 руб. Но вначале-то было 30 руб.! Куда делся 1 руб.?

3) Жили-были два пастуха, Иван да Петр, пасли они овец. И вот как-то Иван говорит: «Слушай, отдай мне одну овцу, тогда у меня овец будет в 3 раза больше, чем у тебя!». «Нет, – отвечает Петр, – лучше ты мне отдай одну овцу, тогда у нас их станет поровну!»

Сколько овец было у Ивана и сколько у Петра?

Умозаключения из одной посылки просты. Несколько более сложными являются умозаключения из двух посылок. Среди них одно из наиболее распространенных – простой категорический силлогизм Его открыл в наших повседневных рассуждениях и описал Аристотель, и в значительной мере именно поэтому он считается создателем логики как науки. Вот пример простого категорического силлогизма:

Все люди смертны.

Сократ – человек.

Сократ смертен.

Здесь мы видим уже две посылки: «Все люди смертны» и «Сократ – человек». Из этих двух суждений мы выводим новое суждение «Сократ смертей». Если вы обратите внимание на свои рассуждения, то очень скоро обнаружите, что часто используете такой способ вывода.

Понятия, из которых состоят посылки и вывод силлогизма, называются его терминами. В силлогизме всего три термина.

Меньшим термином силлогизма называется субъект вывода. Он обозначается буквой «S», как субъект в структуре простого суждения. Но здесь эта буква обозначает меньший термин, который в посылке может встретиться и на месте предиката. В нашем примере меньшим термином будет понятие «Сократ».

Большим термином силлогизма называется предикат вывода. Он обозначается буквой «P», как предикат в структуре простого суждения, но здесь эта буква обозначает больший термин, который в посылке может стоять и на месте субъекта. В нашем примере большим термином будет понятие «смертны».

Наконец, средним термином силлогизма называется понятие, входящее в обе посылки, но отсутствующее в выводе. Он обозначается буквой «M». В нашем примере средним термином является понятие «люди». (Слова «люди» и «человек» выражают одно и то же понятие, различие между ними носит лишь грамматический характер, не обращайте на него внимания.)

Силлогизм – это умозаключение, говорящее о соотношении объемов входящих в него понятий. Первая посылка говорит о том, что класс людей входит в класс смертных существ; вторая посылка говорит о том, что Сократ входит в класс людей; опираясь на эти два соотношения, мы делаем вывод о том, что Сократ включается в класс смертных существ.

Мы часто строим свои рассуждения в виде простого категорического силлогизма, опираясь на свою интуицию. Но часто ошибаемся при этом. Логика устанавливает некоторые простые правила, которые помогают избежать ошибок и неверных выводов.

Например, в силлогизме должно быть только три термина. Если появляется четвертый термин, силлогизм разрушается: мы не можем найти среднего термина и сделать вывод. Даны вам, скажем, такие посылки:

Все артисты самолюбивы.

Олег Табаков талантлив.

Здесь четыре термина. Какой из них считать средним? Какой меньшим или большим? Это просто два никак не связанных между собой суждения, из которых никакого нового знания извлечь нельзя. Ошибка, связанная с нарушением указанного правила, так и называется – «учетверение терминов». Кажется, что эту ошибку трудно совершить. Однако она встречается довольно часто и обусловлена многозначностью слов нашего повседневного языка. Одно и то же слово в одной посылке может употребляться в одном смысле, а в другой посылке – в ином смысле и выражать, таким образом, два разных понятия. Получается четыре термина, хотя слов-то всего три. Например:

Движение вечно.

Хождение в институт – движение.

Хождение в институт вечно.

Здесь слово «движение» в одной посылке употребляется для выражения философского понятия движения как универсального свойства материального мира, а в другой посылке оно выражает бытовое, обыденное понятие движения. Поэтому и получается нелепый вывод.

Шуба греет.

«Шуба» – русское слово.

Некоторые русские слова греют.

Здесь кавычки нам показывают, что слово «шуба» используется в разных смыслах в первой и второй посылках. Однако в устной речи это различие может остаться незамеченным. Приведенные примеры просты и прозрачны, но во многих случаях учетверение терминов носит более тонкий характер и его нелегко распознать.

Еще одно правило гласит: из двух отрицательных посылок нельзя сделать никакого вывода. Например:

Ярко-красные цветы не имеют запаха.

Этот цветок не имеет запаха.

Можно ли сделать вывод о том, что этот цветок ярко-красный? Нет, он может быть любого цвета.

Другие правила силлогизма столь же просты. Теперь взгляните на четыре следующих силлогизма и попробуйте понять, чем они отличаются друг от друга.

Все рыбы плавают.

Щуки являются рыбами.

Щуки плавают.

Всякий человек имеет две ноги.

Буратино имеет две ноги.

Буратино – человек.

Вы можете заметить, что средний термин в этих примерах стоит в посылках на разных местах. В первом примере средний термин «рыбы» в первой посылке стоит на месте субъекта, а во второй – на месте предиката. Во втором средний термин «имеет две ноги» в обеих посылках стоит на месте предиката. В третьем средний термин «птицы» в обеих посылках стоит на месте субъекта. Наконец, в четвертом примере средний термин «параллелограмм» в первой посылке стоит на месте предиката, а во второй – на месте субъекта. Все это разные способы рассуждения, построенные в виде простого категорического силлогизма. Они называются фигурами силлогизма. Иначе говоря: фигурами силлогизма называются его разновидности, отличающиеся друг от друга расположением среднего термина в посылках. Существует всего четыре фигуры. Вот их схематичное представление: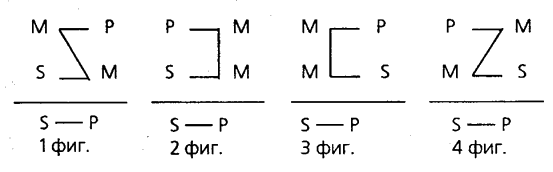

Подставляя вместо букв «S», «P» и «M» различные понятия, мы будем получать рассуждения, имеющие вид одной из фигур силлогизма.

Однако в повседневной речи мы редко пользуемся развернутыми силлогизмами, ибо язык наш – великий лентяй! Он почти никогда не выговаривает полностью всего того, что мы хотим сказать (хотя порой выбалтывает такое, о чем лучше бы умолчать). Обратите внимание на свою речь, на речь ваших друзей и знакомых, и вы легко убедитесь, сколь многое нами не договаривается, подразумевается, как легко ошибиться, домысливая речь собеседника. Вот, например, беседуют два приятеля:

– Ну и чем же закончилась вчера твоя ссора с женой?

– О, я заставил ее встать передо мной на колени.

– Вот как! И что же она сказала?

– Вылезай из-под кровати, подлый трус!

Вот так мы сокращаем и наши силлогизмы, не высказывая в явном виде все его посылки или вывод в надежде на то, что собеседник сам домыслит недостающее звено и поймет нас. Это вполне естественно. Тяжело-разговаривать с человеком, который стремится произнести вслух даже самые очевидные вещи. Он напоминает полковника Фридриха Крауса фон Циллергута из романа Я. Гашека «Похождения бравого солдата Швейка», любившего все пояснять и объяснять и заслужившего вследствие этого славу величайшего осла и зануды. Вряд ли вы долго выдержите такие, например, рассуждения: «Дорога, по обеим сторонам которой тянутся канавы, называется шоссе. Да-с, господа. Знаете ли вы, что такое канава? Канава – это выкопанное значительным числом рабочих углубление. Да-с. Копают канавы при помощи кирок. Известно ли вам, что такое кирка?»

Силлогизм, в котором опущена и лишь подразумевается одна из частей – посылка или вывод, – называется энтимемой. В повседневной жизни мы пользуемся сокращенными силлогизмами – энтимемами. Это вполне естественно, но это также служит причиной многих ошибок в наших рассуждениях. Когда силлогизм представлен в полном виде, ошибку легко заметить. Но если какая-то его часть опущена, подразумевается, то именно в ней-то и может скрываться ошибка – либо подразумеваемая часть ложна, либо образует неправильный силлогизм. Допустим, я высокомерно заявляю:

«Этот человек глуп, так как он не знает логики!» Это энтимема.

Восстановим подразумеваемую посылку и запишем полный силлогизм:

Всякий человек, не знающий логики, глуп.

Этот человек не знает логики.

Этот человек глуп.

Сразу же становится видно, что подразумеваемая и восстановленная посылка ложна: далеко не каждый человек, не знающий логики, глуп. Многие люди, никогда не изучавшие логику, обладают тем не менее острым и проницательным умом. И наоборот, некоторые люди всю жизнь занимаются логикой, оставаясь при этом весьма недалекими личностями. Логика помогает нашему разуму, но все-таки разум нужно иметь – как нужно иметь ноги, чтобы тебе помогали костыли.

4) Произошла кража, и были задержаны трое подозреваемых. Один из них вор, который постоянно лжет; другой является соучастником и лжет лишь иногда; третий – честный человек, который никогда не лжет. Дознание началось с вопросов о профессии каждого из задержанных. Следователь получил такие ответы.

Щукин: я маляр, Карасев – настройщик роялей, а Окунев – дизайнер.

Карасев: я врач, Окунев – страховой агент. Что же касается Щукина, то, если вы его спросите, он ответит, что он маляр.

Окунев: Карасев – настройщик роялей, Щукин – дизайнер, а я – страховой агент.

По этим ответам следователь догадался, кто есть кто. Догадайтесь и вы!

Если вы учились в школе, то, по-видимому, помните простую схему рассуждения, имеющую вид: «Если а, то в; если в, то с; следовательно, если а, то с». Скажем, в арифметике это рассуждение представлено принципом: если две величины порознь равны третьей, то они равны между собой. Такого рода рассуждения называются условными силлогизмами: здесь и посылки и вывод являются условными суждениями. Вот пример условного силлогизма, взятый из рассказа В. Билибина, русского писателя начала XX в.:

«Если бы на свете не существовало Солнца, то пришлось бы постоянно жечь свечи и керосин.

Если бы пришлось постоянно жечь свечи и керосин, то чиновникам не хватало бы их жалованья и они брали бы взятки. Следовательно, чиновники не берут взяток потому, что на свете существует Солнце».

Еще больше распространены рассуждения, в которых одна посылка является условным суждением, вторая посылка и вывод – простыми категорическими суждениями. Такое рассуждение называется условно-категорическим силлогизмом. Например, когда вы чувствуете недомогание, то первое, что вы делаете, ставите себе градусник. И когда вы приходите в поликлинику, то вам опять-таки сначала ставят градусник. Мы исходим при этом из посылки: «Если у человека повышена температура, то человек болен». Если у вас действительно обнаруживается повышенная температура, то вас признают больным, освобождают от работы или учебных занятий, ваши домашние ходят вокруг вас на цыпочках и стараются напоить вас чаем с малиной При этом мы рассуждаем следующим образом:

Если у человека повышена температура, то человек болен.

У данного человека повышена температура. Следовательно, данный человек болен. Представим наше рассуждение в символической форме. Обозначим суждение «У человека повышена температура» буквой A, суждение «Человек болен» – буквой B. Тогда наше рассуждение получит вид: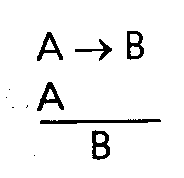

(стрелка «->» читается как «если… то»). Мы помним, что первая часть условной посылки называется основанием, вторая – следствием. Вторая посылка нашего рассуждения утверждает, что основание имеет место, отсюда мы делаем вывод, что и следствие должно иметь место. Рассуждение, имеющее такой вид, называется утверждающим модусом условно-категорического силлогизма (или modus ponens, если воспользоваться латынью): здесь мы от утверждения основания переходим к утверждению следствия условной посылки.

Однако при той же условной посылке рассуждение может протекать иначе. Поставили вам градусник, но температура оказалась нормальной. Отсюда делают вывод, что вы не больны, от занятий вас не освобождают, чаем вас не поят. Рассуждение имеет вид: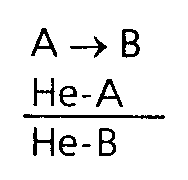

При той же условной посылке можно двигаться к выводу, утверждая или отрицая ее следствие. Таким образом, условно-категорический силлогизм имеет всего четыре модуса: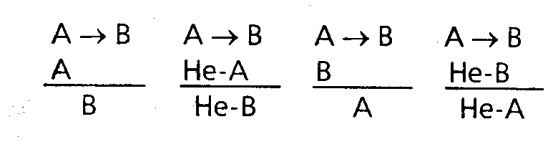

Первый и последний называются «правильными» модусами: они обеспечивают достоверный вывод; второй и третий – «неправильными» модусами: они не дают достоверного вывода – так рассуждать нельзя, это приведет к ошибке, в чем нетрудно убедиться.

Повышенной температуры у вас не обнаружили, но каждый из нас знает, что это вовсе не означает, что вы не больны: многие болезни не сопровождаются повышением температуры. Поэтому вывод о том, что человек не болен, может оказаться ошибочным. В третьем модусе из того, что человек болен, мы делаем вывод о том, что у него должна быть повышена температура. По тем же самым причинам этот вывод может оказаться ошибочным. Наконец, четвертый модус говорит нам, что если человек не болен, то у него нет температуры. Этот вывод вполне достоверен: если вы здоровы, то температура у вас нормальная.

Таким образом, если вы свое рассуждение строите по первому и последнему модусу – вы рассуждаете правильно; если же свое рассуждение вы строите по второму или третьему модусу – вы рискуете совершить ошибку.

5) «Идите сюда, – сказал я как-то трем студентам. – Вот у меня здесь 5 шапок: 3 белые и 2 черные. Закройте глаза, и я надену на каждого из вас шапку. Когда вы откроете глаза, то сможете увидеть, какого цвета шапки на ваших товарищах. Свою собственную шапку вы увидеть не сможете и не увидите, какие шапки остались у меня. Тот, кто догадается, какого цвета на нем шапка, сразу же получит зачет по логике».

Через некоторое время, не обменявшись ни единым словом, студенты закричали: «На мне белая шапка!» Пришлось мне всем троим поставить зачет. А вы бы догадались?

Разделительно-категорический силлогизм есть умозаключение, в котором одна посылка является разделительным суждением, а вторая посылка и вывод – простыми категорическими суждениями.

Например, просыпаетесь вы утром и, еще лежа в постели, начинаете рассуждать: «Сегодня днем я могу пойти на свидание или на занятия. Пойду-ка я на свидание. Следовательно, на занятия я не пойду». Здесь первая посылка вашего рассуждения представляет собой разделительное суждение «Я могу пойти на свидание (A) или пойти на занятия (B)», символически: A v B. Вторая посылка утверждает одну из возможностей, указанных в разделительной посылке: «Я пойду на свидание» (A). Вывод отрицает вторую возможность: «Следовательно, я не пойду на занятия» (Не-B). Ясно, что вы можете рассуждать и несколько иначе: «Нет, на свидание я не пойду. Следовательно, я пойду на занятия». Символически эти два способа рассуждения можно представить следующим образом: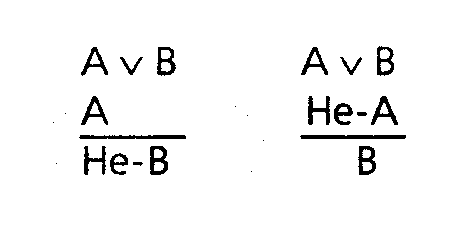

Они называются модусами разделительно-категорического силлогизма. Первый модус называется утверждающе-отрицающим, второй – отрицающе-утверждающим. Оба модуса могут приводить как к верным, так и к ошибочным заключениям. Для того чтобы не совершать ошибок при рассуждениях, имеющих вид разделительно-категорического силлогизма, нужно выполнить требование к разделительной посылке. При утверждающе-отрицающем модусе разделительная посылка должна быть строго разделительной, т.е. альтернативы должны исключать друг друга. Если это требование не соблюдено, вывод может оказаться ошибочным. Например, встречаете вы знакомого, идущего с дамой, и думаете: «Эта дама ему мать или жена». Выясняется, что дама приходится ему женой. «Ага, – делаете вы вывод, – значит, она ему не мать». Это – утверждающе-отрицающий модус, и его разделительная посылка является строго разделительной. Вывод вполне достоверен.

Но вот другой случай. Вы видите вашего знакомого, с изможденным видом бредущего по улице. «Он болен или беден», – думаете вы. Выясняется, что ваш знакомый давно и неизлечимо болен. «Значит, он не беден», – делаете вы вывод. Увы, разделительная посылка не является строго разделительной: болезнь и бедность отнюдь не исключают друг друга, особенно в наше время. Вывод может оказаться ошибочным.

Для отрицающе-утверждающего модуса требование таково: разделительная посылка должна быть исчерпывающей, т.е. должна охватывать все возможности, существующие в данной области рассуждений. В противном случае вывод может оказаться неверным.

Логическая структура именно этого модуса часто лежит в основе многих детективных сюжетов и реальной следственной практики. Совершено преступление, и следователь очерчивает круг возможных участников преступления. Дальнейшая его работа или развитие сюжета заключаются в том, что он проверяет подозреваемых и по одному отсеивает их: этот был болен, тот сидел в тюрьме в момент совершения преступления, того видели несколько человек в другом месте и т.д. Кто останется – тот и преступник. Это и есть отрицающе-утверждающий модус: преступление мог совершить A или B; A не мог совершить преступления, следовательно, его совершил B.

Хорошо, если в разделительной посылке перечислены все возможные участники преступления. А если нет? Осуждают B, а через некоторое время выясняется, что следствие упустило из виду некоего C, который и является подлинным преступником: в разделительной посылке рассуждения были учтены не все возможности. Ошибся следователь, мог ошибиться и суд. Поэтому сначала нужно доказать, что разделительная посылка является исчерпывающей, и только потом делать вывод. Тогда он будет вполне достоверным.

Конечно, в повседневной жизни и в профессиональной деятельности мы не ограничиваемся теми простыми выводами, с которыми познакомились. Мы можем соединять и комбинировать их самыми разнообразными способами, например, в одном рассуждении можно соединить условно-категорический и разделительно-категорический силлогизмы, тогда мы получим то, что называют дилеммой:

Если пойдешь направо, коня потеряешь. Если пойдешь налево, голову потеряешь. Но нужно идти направо или налево. Придется потерять коня или голову.

Но сложные комбинации умозаключений можно разложить на их простые формы и, таким образом, проверить правильность наших рассуждений.

6) Зашли как-то три крестьянина на постоялый двор. Попросили они хозяйку сварить им чугунок картофеля, а сами повалились спать. Хозяйка сварила картофель и поставила чугунок на стол.

Проснулся один крестьянин, посчитал количество картофелин и съел ровно 1/3 часть. После этого он опять улегся спать. Проснулся другой крестьянин, посчитал картофелины и, думая, что никто еще не ел, съел ровно 1/3 часть. И тоже лег досыпать. Наконец, проснулся третий крестьянин, посчитал количество картофелин и, думая, что никто еще не ел, съел ровно 1/3 часть. Тут проснулись и его товарищи. Заглянули в чугунок, а там осталось всего 8 картофелин.

Спрашивается: сколько всего картофелин сварила хозяйка? Сколько штук съел каждый крестьянин? Сколько еще должен съесть каждый крестьянин, чтобы всем досталось поровну?

7) Жил-был один дехканин, и было у него 17 основ и 3 сына. Умирая, он завещал поделить ослов между сыновьями таким образом: 1/2 – старшему сыну; 1/3 – среднему и 1/9 – младшему. Кинулись братья делить наследство, да что-то никак не получается: не рубить же осла на части! Позвали судью на помощь, но и тот ничего не смог придумать. Кто-то посоветовал братьям обратиться за помощью к одному мудрому старцу, живущему в соседней деревне. Тот приехал, разделил ослов между братьями так, как завещал отец, и уехал, провожаемый благодарностями.

Как сумел мудрец выполнить завещание отца?

Откуда берутся посылки дедуктивных выводов? Что дает нам основание считать их истинными? Конечно, иногда их можно вывести дедуктивно из более общих суждений и посредством этого обосновать их истинность. Однако рано или поздно мы дойдем до таких суждений, для обоснования которых нет более общих посылок, следовательно, их истинность нельзя обосновать дедуктивно. В таких случаях мы прибегаем к помощи индукции.

Индуктивными называют умозаключения, расширяющие наше знание и дающие не достоверный, а лишь вероятный вывод. Посылки индуктивного рассуждения лишь в той или иной степени подтверждают или делают вероятным заключение, но отнюдь не обеспечивают его достоверности. Наиболее типичным индуктивным заключением является вывод от частных случаев к общему утверждению.

В повседневной жизни мы на каждом шагу делаем такие выводы. Когда вы приходите в некое государственное учреждение и даете взятку сначала одному чиновнику, затем другому, вы думаете про себя: «Все чиновники здесь – взяточники!» Или девушка, встретив одного молодого человека и разочаровавшись в нем, затем встретив другого, быть может, уже не столь молодого человека, и вновь испытав разочарование, порой приходит к выводу:

«Все мужчины – подлецы!»

Различают популярную и научную индукцию. При популярной индукции мы спешим сделать обобщение, опираясь на первые попавшиеся частные случаи. Наши примеры как раз демонстрируют индукцию такого рода. Достоверность вывода при популярной индукции весьма невысока, здесь очень легко совершить ошибку, что мы обычно и делаем.

Если же мы сознательно стремимся повысить достоверность индуктивного вывода и принимаем для этого некоторые меры, то такая индукция называется научной. В частности, желательно исследовать как можно больше представителей того класса предметов, к которому относится обобщение. Далее, изучаемые факты должны быть как можно более разнообразными. Наконец, эти факты должны быть типичными для данного класса явлений. При соблюдении этих условий достоверность индуктивного вывода существенно повышается. Так, если бы вы захотели сделать свой вывод о чиновниках данного учреждения более достоверным, вам следовало бы не ограничиваться одним-двумя встреченными вами чиновниками, а познакомиться с большим их количеством, причем принадлежащими к разным ступеням чиновничьей иерархии. Многочисленные примеры подобных выводов можно найти в социологии: стараясь обеспечить достоверность своих утверждений, социолог, по сути, заботится о соблюдении правил научной индукции.

Однако следует помнить о том, что и при соблюдении указанных правил мы можем приходить к ошибочным заключениям. Частые ошибки тех же социологов это наглядно демонстрируют. Но вот пример, придуманный физиками, иллюстрирующий, как обстоит дело в естествознании: «Употреблять в пищу огурцы опасно – с ними связаны все телесные недуги и вообще людские несчастья. Практически все люди, страдающие хроническими заболеваниями, ели огурцы. 99,9% всех людей, умерших от рака, при жизни ели огурцы. 99,7% всех лиц, ставших жертвами авто- и авиакатастроф, употребляли в пищу огурцы в течение двух недель, предшествовавших фатальному несчастному случаю. 93,1% всех несовершеннолетних преступников происходят из семей, где огурцы потребляли постоянно». Этот пример показывает, как легко оснастить ошибочную гипотезу статистическими данными и выдать глупость за научную истину.

Всегда следует помнить о том, что как бы хорошо ни был обоснован индуктивный вывод, сколь бы многочисленными ни были свидетельства в его пользу, с логической точки зрения он всегда остается проблематичным. Поэтому всякий выход за пределы имеющегося знания, всякая попытка получить новое знание связана с риском – с риском ошибиться. Но именно благодаря этому история человеческого познания представляет собой не унылую последовательность неизменных успехов, а драматическое приключение, в котором победы сменяются поражениями, взлеты – падениями, успехи – разочарованиями. Именно риск делает научную игру столь увлекательной и азартной.

1) Эта задача решается просто: нужно переставлять часовых из середины бастиона на его углы, как показано на следующих рисунках: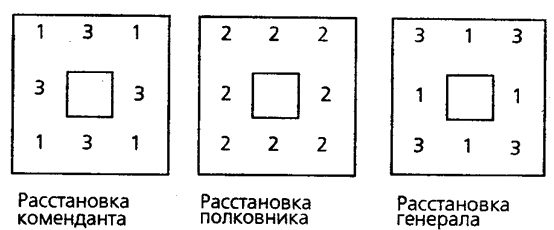

2) К сожалению, здесь простой и наглый обман. Путешественники действительно заплатили 27 руб. Но это и все, никаких 30 руб. уже нет! Из этих 27 руб. хозяйка взяла себе 25 руб. и 2 руб. осталось у мальчика. На каком основании к этим 27 руб. я добавляю еще 2 руб.? Откуда я их взял? Где они? И деньги хозяйки, и деньги мальчика уже посчитаны – они в уплаченных 27 руб. Я выдумал эти 2 руб., чтобы ввести вас в заблуждение.

3) Для решения этой задачи достаточно несложных арифметических действий. Если Иван отдаст 1 овцу Петру, то овец у них станет поровну. Это позволяет нам составить равенство: овцы Петра + 1 = овцы Ивана – 1. Отсюда мы легко заключаем, что у Ивана на 2 овцы больше. Дальнейшее в том же духе. Ответ: у Петра было 3 овцы, у Ивана – 5.

4) Не знаешь, с чего начать. Но есть одна зацепка, помогающая размотать клубок. Карасев сказал: «Если вы спросите у Щукина о его профессии, он ответит, что он маляр». И Щукин действительно сказал, что он маляр! Значит, Карасев хотя бы одну правду сказал, следовательно, он не может быть вором, который всегда лжет. Может быть, Карасев – соучастник, который иногда говорит правду, а иногда лжет? Тогда вором и честным человеком должны быть Щукин и Окунев, и их ответы должны полностью отличаться один от другого, так как один из них всегда говорит правду, а другой постоянно лжет. Нет, такого не получается: ответы Щукина и Окунева в одном пункте совпадают. Следовательно, только Карасев может быть честным человеком и все, что он сказал, – правда. Ответы Окунева в одном пункте совпадают с ответами Карасева, следовательно, Окунев – соучастник преступления. И естественно, Щукин не может быть никем иным, как вором.

5) Обозначим студентов буквами A, B, C и поставим себя на место A. Он рассуждает так: «Я вижу перед собой две белые шапки. Значит, на мне белая или черная шапка. Если на мне черная шапка, то B видит перед собой черную и белую шапки. Но B ведь тоже рассуждает: „Если бы на мне была черная шапка, то C видел бы перед собой две черные шапки и сразу же догадался бы, что на нем самом белая шапка. Но C молчит, значит, на мне – белая шапка“. Таким образом, – продолжает рассуждать A, – если бы на мне была черная шапка, то B уже догадался бы, что на нем самом должна быть белая шапка. Но B молчит. Значит, он не видит на мне черной шапки. Следовательно, на мне – белая шапка!» Так рассуждал каждый из них, а поскольку все студенты соображали одинаково быстро, они одновременно решили задачу.

6) Здесь важна логика рассуждения, приводящего к решению. Нужно двигаться с конца к началу. В конце осталось 8 картофелин, что равно 2/3 того количества, которое обнаружил в чугунке третий крестьянин. Значит, всего он обнаружил 12 штук. Но это равно 2/3 того количества, которое нашел второй крестьянин. Значит, там было 18 штук. Опять-таки, это равно 2/3 того количества картофеля, которое обнаружил первый крестьянин. Следовательно, первый нашел в чугунке 27 картофелин. Столько картофелин сварила хозяйка. Первый съел 9 штук и больше ни на что претендовать не может. Второй съел 6 штук, и ему еще полагается 3 картофелины. Третий съел всего 4 штуки и должен получить еще 5 картофелин.

7) Эта задача сложная, боюсь, не все с ней справились. Действительно, 17 не делится ни пополам, ни на три части, ни на девять частей. Но вы помните: мудрец приехал, он приехал на осле! Добавив своего осла к ослам братьев, он получил 18 ослов. Половину, т.е. 9 ослов, он отдал старшему брату; третью часть, 6 ослов, он отдал среднему брату и девятую часть – двух ослов – передал младшему. Итак: 9 + 6 + 2 = 17. После этого он сел на своего осла и уехал.