Образование винтовой линии. Рассмотрим рисунок 113а на нем точка М двигается равномерно по некоторой окружности, которая представляет собой сечение круглого цилиндра плоскостью Р. Здесь эта плоскость перпендикулярна его оси.

Допустим, что и сама окружность движется равномерно вверх или вниз по поверхности цилиндра. При этом плоскость Р, которая содержит окружность, будет оставаться всё время параллельной самой себе. Пять различных положений плоскости, которая содержит движущуюся точку, показаны на рисунке 113 б.

Вследствие этих двух равномерных движений данная точка М пройдет некоторую пространственную кривую М₁М₂М₃М₄М₅. На рисунке 113в показана эта линия, которая располагается на поверхности цилиндра и носит название цилиндрической винтовой линии. Она не может быть совмещена с плоскостью. На рисунке 113 г показано наглядное представление о винтовой линии, которое дает пружина.

Особое внимание следует уделить рассмотрению способности линии перемещаться по самой себе. Прямая линия и окружность обладают способностью перемещаться по самим себе, вследствие чего цилиндрическая винтовая линия также может перемещаться по самой себе. Например, завинчивая металлический винт в специально приготовленное для него отверстие, мы наблюдаем скольжение одной винтовой поверхности по другой.

Шаг винтовой линии. Точка, сделав полный оборот вокруг цилиндра, будет подниматься вверх или опускаться вниз на некоторое расстояние, которое будет одним и тем же для каждого полного оборота точки (рис. 114). Шагом винтовой линии называется подъем точки за один оборот. Витком называется часть винтовой линии, которая описывается точкой за один оборот.

Правая и левая винтовые линии. На рисунке 114 будем рассматривать цилиндр со стороны основания в то время, когда точка, перемещаясь по винтовой линии, будет удаляться от наблюдателя. Вероятны два случая: движение по часовой стрелке или против неё. Если движение проходит по часовой стрелке, то будет иметь место правая винтовая линия (рис. 114а), а если против часовой стрелки – левая (рис. 114б). На рисунке 114(а-б) в первом случае видимая часть линии будет подниматься слева направо, а во втором – справа налево.

Проекции винтовой линии. Одна проекция прямого кругового цилиндра, на котором расположена винтовая линия, является окружностью, а другая – прямоугольником (рис. 114). Нужно построить фронтальную проекцию правой винтовой линии.

Допустим, движение точки начинается на основании цилиндра в точке 1 (рис. 114). Будем делить шаг винтовой линии и окружность основания на одинаковое число равных частей. На рисунке 114 этих частей 12. За полный оборот точка будет подниматься на величину шага. Следовательно, за 1/12 часть оборота она поднимется на 1/12 часть шага (точка 2).

Затем следует провести через точки деления шага 1?, 2,…, 12 горизонтальные прямые, а через точки деления окружности 1, 2,…, 12 – вертикальные. Точки фронтальной проекции винтовой линии 1?, 2?,…, 12? будут иметь место в пересечении горизонтальных и вертикальных прямых, которые проходят через деления шага и окружности и имеют одинаковые номера. Эти точки 1?, 2?,…, 12? следует соединить плавной линией, которая будет представлять собой фронтальную проекцию винтовой линии. Этой линией будет синусоида.

При сравнении фронтальных проекций правой и левой винтовых линий убеждаемся в том, что форма кривой одна и та же, лишь видимая часть правой винтовой линии стала невидимой у левой, и наоборот. Кроме того, изменился порядок нумерации точек деления окружности на горизонтальной проекции. Для правой винтовой линии номера точек будут возрастать по часовой стрелке, а для левой будут убывать против часовой стрелки.

Развертка поверхности цилиндра с нанесённой на ней винтовой линией. Если развернуть на плоскость боковую поверхность цилиндра с нанесенной на ней винтовой линией, то винтовая линия предстанет в виде прямой линии (рис. 115), поскольку величина подъема точки пропорциональна ее перемещению вдоль окружности.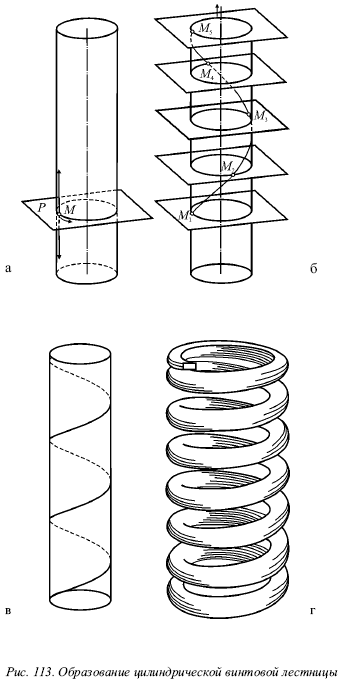

В соответствии с этим несложно изготовить модель винтовой линии, нужно только взять прямоугольник с проведенной в нем диагональю и свернуть его в виде цилиндра. При этом диагональ прямоугольника будет образовывать один виток винтовой линии.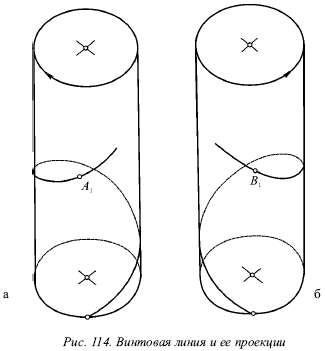

Угол носит название угла подъема винтовой линии, его тангенс выражается формулой: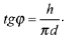

Метод проведения вспомогательных плоскостей применяется при построении линии пересечения поверхностей двух тел вращения. Суть этого метода заключается в следующем. Проводят вспомогательную плоскость А (рис. 115) таким образом, чтобы каждое из данных тел она пересекала по такой линии, построение которой не является сложным. Строят данные две линии, по которым вспомогательная плоскость пересекает поверхность каждого из тел, а точки пересечения этих линий относятся к искомой линии пересечения данных поверхностей. Следовательно, важно подобающим образом провести вспомогательную плоскость.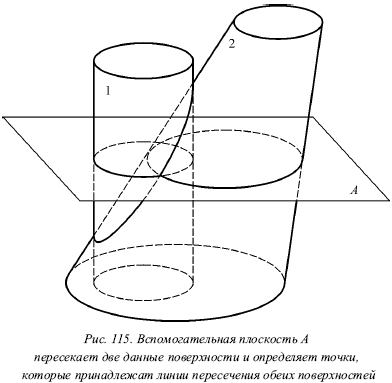

Лучше всего начинать построение с нахождения характерных точек, к которым главным образом относятся точки, отделяющие видимую часть линии от невидимой на каждой проекции. Характерными точками могут быть и самая верхняя точка линии, и самая нижняя, и самая передняя, и самая задняя и т. д. После установления всех характерных точек и указания достаточного количества промежуточных, проводят линию, которая соединяет эти точки.