VI

Нелогичное развитие: в трясине математического анализа

Начинать исследование можно по-разному. Все равно начало почти всегда оказывается весьма несовершенной, нередко безуспешной попыткой. Есть истины, как страны, наиболее удобный путь к которым становится известным лишь после того, как мы испробуем все пути.

Кому-то приходится, рискуя собой, сходить с проторенной дороги, чтобы указать другим правильный путь… На пути к истине мы почти всегда обречены совершать ошибки,

(Дени Дидро)

Математический анализ, ядро которого составляет дифференциальное и интегральное исчисление — самая тонкая область всей математики, — был построен на совсем не существующих логических основаниях арифметики и алгебры и на не вполне ясных основах евклидовой геометрии. Если вспомнить о замеченных нами недостатках в сравнительно простых разделах математики, то нетрудно представить себе, какого напряжения сил и способностей потребовало от математиков создание основной системы понятий и логической структуры дифференциального и интегрального исчисления. Именно так и обстояло дело в действительности.

В основе математического анализа лежит понятие функции. Не стремясь к особой строгости, функцию можно описать как зависимость между переменными. Поясним это на простом примере. Если, скажем, с крыши дома бросить мяч, то и расстояние, проходимое им в процессе падения, и время падения будут возрастать. Расстояние и время — переменные, а функция, связывающая расстояние и время (если пренебречь сопротивлением воздуха), определяется формулой d = 4,9t², где t — время падения (в секундах), а d — расстояние (в метрах), пройденное мячом за время t с момента падения.

Происхождение любой важной идеи всегда можно проследить, углубляясь в историю на десятилетия, если не на века. В полной мере это относится и к понятию функции. Тем не менее явный смысл понятие функций обрело лишь в XVII в. Мы не будем здесь вникать в подробности этого процесса. Для нас гораздо важнее другое: хотя понятие функции весьма «прямолинейно» и, казалось бы, не таит в себе никаких «подводных камней», но даже и простейшие функции охватывают все типы вещественных чисел. Так, в приведенном нами примере мы могли бы поинтересоваться значением d при t = v2. Точно так же можно было бы спросить, чему равно t, когда d равно, скажем, 50: при d = 50, как нетрудно видеть, t = v(50/4,9), т.е. принимает иррациональное значение. Но, как мы уже отмечали, в XVII в. понятие иррационального числа еще не получило должного истолкования. Следовательно, едва зародившейся теории функций явно недоставало логических обоснований, как не было их и у арифметики. Однако, поскольку к середине XVII в. математики привыкли свободно обращаться с иррациональными числами, на отсутствие таких обоснований никто не обращал внимания.

Две проблемы привлекали к себе внимание величайших математиков XVII в., наиболее известными среди которых были Кеплер (1571-1630), Декарт (1596-1650), Бонавентура Кавальери (1598-1647), Ферма (1601-1665), Блез Паскаль (1623-1662), Джеймс Грегори (1638-1675), Жиль Персон, называвший себя де Робервалем{76} (1602-1675), Христиан Гюйгенс (1629-1695), Исаак Барроу (1630-1677), Джон Валлис (1616-1703) и, конечно же, Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716). Каждый из этих ученых по-своему подошел к проблемам определения и вычисления производной и определенного интеграла. Одни из творцов дифференциального и интегрального исчисления рассуждали чисто геометрически, другие — чисто алгебраически, третьи использовали смешанный алгебро-геометрический подход. Нас будет интересовать, насколько создателям новых методов исчисления удалось приблизиться к образцам математической строгости. Для этого достаточно обратиться к нескольким наиболее типичным примерам, поскольку многие из предложенных методов были очень ограниченными и особого упоминания не заслуживают.

Природу производной легче всего понять, если представить ее как скорость (именно так поступил Ньютон). Если тело преодолевает расстояние 20 м за 4 с, то его средняя скорость равна 5 м/с, а если тело движется равномерно, то его средняя скорость на протяжении 4 с совпадает с мгновенной, т.е. со скоростью в любой данный момент. Однако движения чаще всего неравномерны. Тело, падающее на Землю, снаряд, вылетевший из пушки, планета, обращающаяся вокруг Солнца, — все движутся неравномерно: их скорость непрерывно меняется. Во многих случаях необходимо знать значения скорости движения в разные моменты времени. Например, жизненно важно знать, с какой скоростью пуля долетает до человека; если эта скорость близка к 0 м/с, то на землю упадет пуля, тогда как при скорости порядка 300 м/с на землю падает человек. По самому своему смыслу момент времени есть не что иное, как «нулевой промежуток» времени, а за нулевое время тело, разумеется, проходит равное нулю расстояние. Следовательно, если бы мы решили вычислять мгновенную скорость так, как вычисляют среднюю скорость, т.е. деля пройденное расстояние на требующееся для его прохождения время, то получили бы выражение 0/0, а такое отношение смысла не имеет.

Выход из создавшегося затруднения, который промелькнул в сознании математиков XVII в., но не был уяснен ими до конца, состоит в следующем. Предположим, что требуется вычислить скорость, которую приобретает свободно падающее тело ровно через 4 с после начала падения. Выбрав любой конечный промежуток времени (в отличие от нулевого промежутка — момента времени), в течение которого тело падает, и разделив на него расстояние, пройденное телом за это время, мы получим среднюю скорость за выбранный промежуток времени. Вычислим теперь среднюю скорость за промежутки времени, следующие за 4-й секундой и имеющие продолжительность ¹/₂, ¹/₄, ¹/₈, … с. Ясно, что, чем меньше промежуток времени, тем ближе средняя скорость к мгновенной скорости тела через 4 с после начала падения. По-видимому, нам остается лишь вычислить средние скорости и посмотреть, к какой величине они стремятся. Эта величина и определяет мгновенную скорость, которой тело достигает к концу 4-й секунды свободного падения. Предложенная схема кажется достаточно разумной, хотя и таит в себе, как мы увидим в дальнейшем, некоторые сложности. Как бы то ни было, скорость к концу 4-й секунды свободного падения, если она вычислима, называется производной функции d = 4,9t² при t = 4.

Трудности, связанные с определением производной, станут более понятными, если от словесного описания производной перейти на язык символов. Математическое определение производной, которое, по существу, и было в конце концов принято, принадлежит Ферма. Вычислим скорость, приобретаемую через 4 с после начала свободного падения мячом, движение которого описывается функцией

d = 4,9t². (1)

При t = 4 получаем: d = 4,9•4² = 78,4 м. Пусть h — приращение времени. За время (t + h) с мяч пролетит в свободном падении расстояние 78,4 м плюс некоторое дополнительное расстояние k. Следовательно,

78,4 + k = 4,9 (4 + h)² = 4,9(16 + 8h + h²),

или

78,4 + k = 78,4 + 39,2h + 4,9h².

Вычтем из правой и левой частей последнего равенства по 78,4:

k = 39,2h + 4,9h².

Итак, средняя скорость за время h с свободного падения равна

k/h = (39,2h + 4,9h²)/h. (2)

При рассмотрении этой простой функции и других функций Ферма повезло: числитель и знаменатель правой части ему удалось разделить на h, получив

k/h = 39,2 + h. (3)

Затем Ферма положил приращение h равным нулю и получил, что скорость тела через 4 с после начала свободного падения такова:

d^• = 39,2 м/с. (4)

(d^• — обозначение производной, предложенное Ньютоном). Итак, d^• — производная от d = 4,9t² при t = 4.

Против предложенного Ферма метода вычисления производной можно возразить, указав, что приращение h должно быть отлично от нуля, ибо выполнение таких операций, как деление числителя и знаменателя на h, возможно только при h, отличном от нуля. Но тогда и равенство (3) справедливо только при h, отличном от нуля. Следовательно, мы не можем полагать в (3) значение h равным нулю и делать из этого предположения какие бы то ни было выводы. Кроме того, в случае такой простой функции, как d = 4,9t², соотношение (2) после сокращения правой части на h переходит в соотношение (3). В случае же более сложных функций нам пришлось бы иметь дело с выражением типа (2). При h = 0 правая часть (2), выражающая предельное значение средней скорости k/h, обращается в неопределенность 0/0.

Ферма никогда не занимался обоснованием своего метода, и, хотя он по праву может быть назван одним из создателей математического анализа, ему не удалось продвинуться здесь особенно далеко. Он был достаточно осторожен, чтобы пытаться формулировать общие теоремы, если сознавал, что какая-либо идея не обоснована им полностью.{77} Ферма довольствовался тем, что предложил правильный алгоритм, которому смог дать геометрическую интерпретацию, и надеялся, что когда-нибудь удастся найти полное геометрическое обоснование предложенного им метода.

Второе понятие математического анализа, доставившее немало хлопот его создателям, — (определенный) интеграл — встречается, например, при вычислении площадей фигур, ограниченных целиком или частично кривыми линиями, объемом тел, ограниченных изогнутыми поверхностями (не плоскостями!), а также центров тяжести тел различной формы. Чтобы понять, какого рода трудности встречаются при использовании понятия определенного интеграла, рассмотрим вычисление площади криволинейной трапеции.

Предположим, требуется найти площадь криволинейной трапеции DEFG (рис. 6.1), ограниченной дугой FG кривой, задаваемой уравнением y = x², отрезком DE оси x и вертикальными отрезками DG и EF. В этом случае, как и при вычислении производной, мы хотим найти интересующую нас величину методом все более точных последовательных приближений. Нечто подобное предприняли математики XVII в.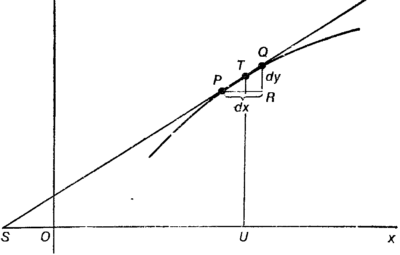

Рис. 6.4. Характеристический треугольник PQR.

Лейбниц широко использовал понятие интеграла и независимо пришел к идее суммирования элементарных прямоугольников, на которые разбивается криволинейная трапеция [ср. (7)]. Но переход от суммы конечного числа прямоугольников к сумме бесконечно большого числа прямоугольников был не вполне понятен. По утверждению Лейбница, сумма элементарных прямоугольников превращалась из конечной в бесконечную, когда ширина h прямоугольников становилась «бесконечно малой». Для бесконечной суммы бесконечно малых величин — интеграла — Лейбниц ввел специальное обозначение ?ydx. Он научился вычислять такие интегралы и независимо открыл основную теорему интегрального исчисления, утверждающую, что вычисление интеграла представляет собой операцию, обратную нахождению производной (антидифференцирование). После примерно двенадцати лет упорной работы над своим вариантом математического анализа Лейбниц опубликовал первую работу о новом исчислении в журнале Acta eruditorum («Журнал ученых») за 1684 г. Наиболее выразительный отзыв на эту работу Лейбница дали его друзья, братья Якоб и Иоганн Бернулли, заявив, что это «не столько загадка, сколько объяснение».

Идеям Ньютона и Лейбница недоставало ясности, и критики не замедлили воспользоваться этим. Ньютон не снисходил до ответа на критические замечания, тогда как Лейбниц считал своим долгом ответить на возражения критиков. Его попытки объяснить в частной переписке свое понимание бесконечно малых величин столь многочисленны, что для подробного разбора их понадобилось бы немало страниц. В статье, опубликованной в томе Acta eruditorum за 1689 г., Лейбниц утверждал, что бесконечно малые — не действительные, а некие фиктивные числа. Но эти фиктивные, или мнимые, числа подчиняются тем же правилам арифметики, что и обычные числа.

В той же статье Лейбниц, исходя из геометрических соображений, доказывал, что высший дифференциал (бесконечно малая более высокого порядка, чем первый), например (dx)², относится к низшему дифференциалу dx, как точка к прямой, и что dx относится к x, как точка к земному шару или радиус Земли к радиусу небесной сферы. Отношение двух бесконечно малых Лейбниц мыслил как отношение двух неопределенностей или бесконечно малых величин, которое, однако, можно выразить через конечные величины. Например, геометрически отношение dy к dx есть не что иное, как отношение ординаты к подкасательной (TU к SU на рис. 6.4).

Одним из критиков, выступивших против Лейбница, был Бернгардт Нювентидт (1654-1718). Ответ Лейбница ему был опубликован в Acta eruditorum за 1695 г. Лейбниц обрушился на ревнителя математической строгости, справедливо заметив, что чрезмерная скрупулезность не должна отвращать нас от плодов нового открытия. Лейбниц утверждал, что его метод отличается от метода Архимеда только терминологией, и считал, что избранная им терминология в большей мере отвечает искусству совершать открытия. Термины «бесконечная» и «бесконечно малая» относятся к величинам, которые можно считать сколь угодно большими или сколь угодно малыми, когда требуется показать, что совершаемая ошибка меньше «наперед заданного числа» (т.е. что ошибки нет). Предельные величины, т.е. все эти «действительные бесконечности» и «бесконечно малые», можно использовать как удобный рабочий инструмент в вычислениях, подобно тому как алгебраисты с превеликой пользой используют мнимые корни. (Напомним, что во времена Лейбница мнимые корни имели весьма шаткий статус.)

В письме к Валлису, написанном в 1699 г., Лейбниц дал несколько иное объяснение бесконечно малых:

Бесконечно малые величины полезно рассматривать так, чтобы, когда требуется найти их отношение, их нельзя было считать нулем, но чтобы в то же время ими можно было пренебречь по сравнению с неизмеримо большими величинами. Так, в x + dx величина dx пренебрежимо мала. Иное дело, если нам требуется найти разность между x + dx и x. Точно так же не следует допускать, чтобы xdx и dxdx стояли рядом. Если необходимо продифференцировать [найти производную] ху, то мы пишем: (x + dx)(y + dy) ? xy = xdy + ydx + dxdy. Но член dxdy неизмеримо мал по сравнению с xdy + ydx, и его надлежит отбросить. Итак, в рассмотренном нами частном случае ошибка меньше любой конечной величины.

Так Лейбниц отстаивал законность математических понятий, используемых в созданном им варианте анализа. Поскольку приводимые Лейбницем доводы не удовлетворяли его критиков, он сформулировал философский принцип, известный под названием принципа непрерывности и практически не отличающийся от того, которым пользовался Кеплер. Этот принцип Лейбниц сформулировал с самого начала своей работы по созданию анализа, изложив его в письме Герману Конрингу от 19 марта 1678 г.: «Если переменная на всех промежуточных этапах обладает некоторым свойством, то и ее предел будет обладать тем же свойством».

В письме к Пьеру Бейлю, написанном в 1687 г., Лейбниц сформулировал свой принцип более полно: «В любом переходе, завершающемся неким пределом, допустимо использовать общее рассуждение, которое может включить этот предел». Свой принцип Лейбниц применил к вычислению производной dy/dx для параболы y = x². Получив dy/dx = 2x + dx, Лейбниц заметил: «Согласно нашему постулату, допустимо включать в общее рассуждение и тот случай (рис. 6.5), когда ордината x₂y₂ все более приближается к фиксированной ординате x₁y₁, пока наконец не совпадет с ней. Ясно, что тогда dx становится равным нулю и должен быть отброшен…» Лейбниц умолчал о том, какие значения следует придавать dx и dy, входящим в левую часть равенства dy/dx = 2x + dx, когда dx обращается в нуль.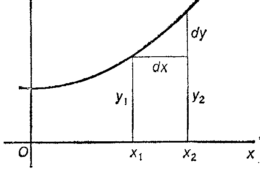

Рис. 6.5. Переход к пределу х₂>x₁ Лейбницу.

Абсолютно равные величины, говорил Лейбниц, имеют, разумеется, разность абсолютно ничтожную.

Тем не менее можно вообразить переход или одно из обращений в нуль, при котором точное равенство или состояние покоя еще не наступило, но достигнуто такое состояние, в котором разность меньше любой заданной величины. В таком состоянии некоторая разность — какая-то скорость, какой-то угол — еще остается, но в каждом случае она бесконечно мала…

Можно ли строго или метафизически обосновать такое состояние мгновенного перехода от неравенства или равенства и сколь законны соображения, использующие бесконечно большие протяженности, продолжающие неограниченно возрастать, или бесконечно малые протяженности, — вопросы, которые мне, по-видимому, придется оставить открытыми…

Вполне достаточно, если каждый раз, когда речь заходит о бесконечно больших (или, точнее, о неограниченных) или о бесконечно малых (т.е. о самых малых из известных нам) величинах, мы условимся понимать, что имеем в виду величины бесконечно большие или бесконечно малые, т.е. сколь угодно большие или сколь угодно малые, вследствие чего допускаемая ошибка может быть меньше заранее заданной величины.

При таких допущениях все правила нашего алгоритма, изложенные в Acta eruditorum за октябрь 1684 г., могут быть доказаны без особого труда.

Далее следовало изложение правил, ничего, впрочем, не добавляющее к их обоснованию.

Сформулированный Лейбницем принцип непрерывности заведомо не был (и ныне не является) математической аксиомой. Тем не менее Лейбниц всячески подчеркивал важность этого принципа и неоднократно использовал его в своих рассуждениях. Так, в письме к Валлису (1698) Лейбниц, отстаивая использование характеристического треугольника (рис. 6.4) как формы, не имеющей размеров и потому остающейся неизменной, когда длины всех сторон треугольника обращаются в нуль, с вызовом спрашивал: «Кто не приемлет форму, лишенную размеров?» В письме к Гвидо Гранди (1713) Лейбниц утверждал, что бесконечно малая — это не простой и абсолютный нуль, а нуль относительный, т.е. исчезающая величина, которая, однако, сохраняет свойство той величины, которая, собственно, исчезает. Но в других случаях Лейбниц признавал, что не верит в истинно бесконечно большие или истинно бесконечно малые величины.

До конца жизни (он умер в 1716 г.) Лейбниц продолжал объяснять, что такое его бесконечно малые и бесконечно большие величины. Однако все эти объяснения были не более убедительны, чем приведенные выше. Созданное Лейбницем дифференциальное и интегральное исчисление не имело ни четко сформулированных понятий, ни обоснований.

У нас может вызвать удивление, что Ньютон и Лейбниц могли довольствоваться столь грубыми рассуждениями. Еще до того, как они приступили к созданию дифференциального и интегрального исчисления, другие великие математики достигли выдающихся успехов, о которых и Ньютон, и Лейбниц, изучавшие труды своих предшественников, безусловно, хорошо знали. Знаменитое высказывание Ньютона «Если я видел дальше других, то лишь потому, что стоял на плечах гигантов» не просто проявление скромности, а констатация факта. Что же касается Лейбница, то он был одним из величайших мыслителей. Мы уже упоминали (гл. III) о том, сколь значительный вклад он внес в развитие различных областей человеческого знания. По широте и силе интеллекта Лейбница можно сравнить разве что с Аристотелем. Разумеется, создание дифференциального и интегрального исчисления потребовало разработки принципиально новых, очень тонких идей, а даже лучшие из умов, способные к величайшим творческим свершениям, не всегда до конца постигают то, что ими же создано.

Ни Ньютон, ни Лейбниц не могли полностью объяснить вводимые ими понятия или обосновать новые операции. Они полагались на плодотворность своих методов, совпадение получаемых ими независимо друг от друга результатов, и продолжали упорно и энергично двигаться вперед, не особенно задумываясь о строгости. Лейбниц, заботившийся о строгости меньше, чем Ньютон, хотя и чаще отвечавший на возражения критиков, считал, что лучшим обоснованием используемых им методов служит их эффективность. Он неоднократно подчеркивал «рецептурную», или алгоритмическую, ценность своих методов. Лейбниц почему-то был убежден, что, сколь бы неясным ни выглядел смысл понятий, результаты рассуждений будут разумны и правильны, если верно сформулировать и надлежащим образом применять правила действий. Подобно Декарту, Лейбниц был человеком проницательным, мыслившим широко. Он предвидел отдаленные последствия новых идей и, не колеблясь, провозгласил рождение новой науки.

Обоснование математического анализа по-прежнему оставалось неясным. Сторонники Ньютона толковали о простых и предельных отношениях; последователи Лейбница предпочитали пользоваться инфинитезимальными, или бесконечно малыми, величинами. Существование столь несхожих между собой подходов осложняло и без того нелегкую работу по обоснованию математического анализа. Кроме того, некоторые английские математики — возможно, в силу традиционной привязанности к греческой геометрии — предъявляли более жесткие требования к строгости доказательств и поэтому с недоверием относились к подходам как Ньютона, так и Лейбница. Другие английские математики, вместо того чтобы заниматься математикой, предпочитали изучать труды Ньютона и поэтому не продвинулись ни на шаг на пути к обоснованию дифференциального и интегрального исчисления. Таким образом, к концу XVII в. математический анализ, так же как арифметика и алгебра, пребывал в состоянии полной неразберихи.

Распространение методов математического анализа на новые области привело к появлению новых понятий и методов, что еще больше осложнило проблему обоснования дифференциального и интегрального исчисления. Примером такого рода дополнительных трудностей могут служить бесконечные ряды. Напомним, с какого рода проблемами столкнулись математики при рассмотрении бесконечных рядов.

Представив функцию 1/(1 + x) в виде (1 + x)^?1 и применив к последней теорему о разложении бинома, получим

1/(1 + x) = (1 + x)^?1 = 1 ? x + x² ? х³ + x⁴ ? …, (8)

где многоточие означает, что число членов, выписываемых по такому же закону, как и несколько первых, можно увеличивать неограниченно. Вводя в математический анализ бесконечные ряды, математики намеревались заменить ими функции в таких операциях, как дифференцирование (нахождение производных) и интегрирование (антидифференцирование), поскольку производить операции с более простыми членами ряда гораздо легче, чем с исходными функциями. Кроме того, ряды позволяли по заданному значению независимой переменной вычислять значения таких функций, как, скажем, sin x. Во всех этих случаях важно знать, что ряд равносилен исходной функции. Но функции при заданном x принимают вполне определенные значения; поэтому прежде всего возникает вопрос: какое значение принимает при заданном x выбранный нами ряд? Иначе говоря, что мы понимаем под суммой ряда и как ее вычислить? Второй, не менее важный вопрос можно было бы сформулировать так: представляет ли ряд функцию при всех значениях x или по крайней мере при всех тех значениях x, при которых функция имеет смысл.

В первой работе по математическому анализу (1669) Ньютон не без гордости ввел бесконечные ряды для упрощения основных операций — дифференцирования и интегрирования. Так, воспользовавшись для интегрирования (антидифференцирования) функции y = 1/(1 + x²) теоремой о разложении бинома, Ньютон получил ряд

y = 1 ? x² + х⁴ ? x⁶ + х⁸ ? …,

который и проинтегрировал почленно. Ньютон обратил внимание на то, что если ту же функцию представить в виде y = 1/(x² + 1), то та же теорема о разложении бинома даст ряд

y = 1/x² ? 1/х⁴ + 1/x⁶ ? 1/х⁸ + ….

Ньютон заметил далее, что при достаточно малом x следует пользоваться первым разложением, а при достаточно большом x — вторым. Из этого видно, что Ньютон интуитивно сознавал важность такого свойства ряда, как сходимость, хотя и не имел о нем ясного представления.

Обоснование, данное Ньютоном производимым им операциям над бесконечными рядами, может служить великолепным образцом логики того времени. В статье 1669 г. Ньютон утверждал:

То, что обычный анализ [алгебра] выполняет с помощью уравнений с конечным числом членов (если это выполнимо), [новый анализ] всегда может выполнить с помощью уравнений с бесконечным числом членов [рядов]; поэтому я, не задумываясь, назвал новое исчисление анализом. Рассуждения в нем не менее надежны, чем в обычном анализе, не менее точны и уравнения, хотя мы, смертные, чей разум ограничен узкими пределами, не можем ни выразить, ни постичь все члены этих уравнений дабы найти из них точные значения тех величин, которые нам нужны.

Для Ньютона бесконечные ряды были частью алгебры — высшей алгебры, изучающей выражения не с конечным, а с бесконечным числом членов.

Подобно Ньютону и Лейбницу, над решением странной проблемы бесконечных рядов бились несколько представителей славного математического рода Бернулли, а также Эйлер, Д'Аламбер и другие математики XVIII в. Применяя бесконечные ряды в анализе, они совершали всевозможные ошибки, предлагали неверные доказательства, приходили к неверным заключениям. Более того, иногда они в обоснование своих результатов приводили рассуждения, которые мы, ретроспективно, можем назвать лишь смехотворными и нелепыми. Даже беглого перечисления таких рассуждений достаточно, чтобы понять, какая сумятица и неразбериха царили тогда в представлениях о свойствах бесконечных рядов.

При x = 1 ряд (8), представляющий функцию 1/(1 + x),

1/(1 + x) = 1 ? x + x² ? х³ + x⁴ ? …, (8)

переходит в ряд

1 ? 1 + 1 ? 1 + 1 ? ….

Вопрос о том, чему равна сумма последнего ряда, порождал бесконечные споры. Если этот ряд записать в виде

(1 ? 1) + (1 ? 1) + (1 ? 1) + …,

то становится ясно, что его сумма должна быть равна нулю. Но если тот же ряд записать как

1 ? (1 ? 1) ? (1 ? 1) ?  …,

то столь же ясно, что сумма ряда должна равняться единице. Однако ясно также и то, что если сумму ряда обозначить через S, то

S = 1 ? (1 ? 1 + 1 ? 1 + …),

или

S = 1 ? S,

откуда S = ¹/₂. Последний результат подкрепляется еще одним доводом. Интересующий нас ряд можно рассматривать как геометрическую прогрессию со знаменателем ?1, а сумма бесконечной геометрической прогрессии с первым членом a и знаменателем r равна a/(1 ? r). В нашем случае сумма равна 1/[1 ? (?1)], или ¹/₂.

Гвидо Гранди (1671-1742) в своем небольшом сочинении «Квадратура окружностей и гипербол» (Quadratura circuit et hyperbolae, 1703) другим методом получил сумму, равную ¹/₂. Полагая в (8) x = 1, он нашел:

¹/₂ = 1 ? 1 + 1 ? 1 + 1 ? ….

Тем самым Гранди утверждал, что сумма ряда равна ¹/₂. Но одновременно он заявлял, что сумма того же ряда равна 0. По мнению Гранди, полученное им «равенство» 0 = ¹/₂ доказывало, что мир мог быть создан из ничего.

В письме к Христиану Вольфу, опубликованному в Acta eruditorum за 1713 г., Лейбниц рассмотрел тот же ряд. Он согласился с выводом Гранди, но считал, что к подобному заключению можно было бы прийти, не обращаясь к исходной функции. Взяв первый член, сумму первых двух, трех, четырех и т.д. членов, Лейбниц получил 1, 0, 1, 0, …. Следовательно, счел он, 0 и 1 равновероятны и их среднее арифметическое, равное ¹/₂, — наиболее вероятное значение суммы ряда. Якоб, Иоганн и Даниил Бернулли, а также Лагранж согласились с доводами Лейбница. Признав, что его доводы носят не столько математический, сколько метафизический характер, Лейбниц сослался на распространенность такого рода аргументации: в математике, по его словам, метафизических истин гораздо больше, чем обычно думают.

В одном из писем, датированных 1745 г., и в работе 1754-1755 гг. Эйлер предпринял попытку решить проблему суммирования рядов. Ряд, сумма которого по мере увеличения числа членов все меньше отличается от некоторого фиксированного числа, называется сходящимся, а само это число — суммой ряда. По Эйлеру, ряд сходится, если члены его монотонно убывают. Ряд, члены которого не убывают и могут даже возрастать, расходится, а так как ряды такого типа порождаются хорошо известными явными функциями, то Эйлер предложил считать суммой ряда значение функции (при соответствующем значении x).

Теория Эйлера породила дополнительные проблемы. Взяв разложение

1/(1 + x)² = (1 + x)^?2 = 1 ? 2x + 3x² ? 4x³ + …,

Эйлер получил при x = ?1

? = 1 + 2 + 3 + 4 + ….

Результат, казалось бы, вполне осмысленный. Но затем Эйлер рассмотрел ряд для функции 1/(1 ? x):

1/(1 ? x) = 1 + x + x² + x³ + …

и получил при x = 2

?1 = 1 + 2 + 4 + 8 + ….

Так как сумма ряда, стоящего в правой части этого ряда, должна превышать сумму предыдущего ряда, Эйлер заключил, что ?1 больше, чем бесконечность. Некоторые из современников Эйлера утверждали даже, что отрицательные числа, которые больше бесконечности, отличаются от отрицательных чисел, меньших нуля. С этим Эйлер не согласился: по его мнению, бесконечность разделяет положительные и отрицательные числа так же, как нуль.

Взгляды Эйлера на сходимость и расходимость рядов были ошибочными. В его время уже были известны ряды с монотонно убывающими членами, тем не менее не имеющие суммы по Эйлеру, — да и ему самому приходилось работать с рядами, которые не были порождены явными функциями. «Теория» бесконечных рядов Эйлера была явно неполной. Кроме того, Николай Бернулли (1687-1759) в ныне утерянном письме (1743), по-видимому, обратил внимание Эйлера на то, что различные аналитические выражения могут порождать один и тот же ряд, и если следовать предложенному Эйлером определению суммы ряда, то этому ряду надлежит приписать различные суммы. В письме Гольдбаху (1745) Эйлер ответил, что Бернулли не привел никаких примеров в подтверждение своих слов и что он, видимо, сам не верит в то, что два истинно различных алгебраических выражения могут порождать один и тот же ряд. Однако Жан Шарль Калле (1744-1799) предложил пример ряда, порождаемого двумя различными функциями. Лагранж пытался опровергнуть пример Калле, но, как выяснилось впоследствии, аргументы Лагранжа были ошибочными.

Подход Эйлера к бесконечным рядам был неадекватен и по другим причинам. Ряды можно дифференцировать и интегрировать, и то, что дифференцирование и интегрирование ряда приводит соответственно к производной и антипроизводной функции, породившей ряд, требует особого обоснования. Несмотря на это, Эйлер провозгласил: «Всякий раз, когда бесконечный ряд получается при разложении некоторого замкнутого выражения [формулы для функции], его допустимо использовать в математических операциях как эквивалент этого выражения даже при тех значениях переменной, при которых ряд расходится». Мы можем обратить себе на пользу расходящиеся ряды, утверждал Эйлер, и защитить их применение от всяких возражений.

Другие математики XVIII в. также сознавали необходимость отличать ряды, называемые ныне сходящимися, от рядов, которые мы называем расходящимися, хотя и не знали, где именно проходит различие между теми и другими. Трудность была вызвана новизной понятия: подобно первопроходцам, математикам XVIII в. приходилось прорубать себе дорогу через девственный лес. Первоначальная идея Ньютона, принятая Лейбницем, Эйлером и Лагранжем (ряд не более чем «длинный» многочлен и, следовательно, относится к области алгебры), не могла служить основой для обоснования операций, производимых с рядами.

В XVIII в. господствовал формальный подход к бесконечным рядам. Математики того времени отменили все ограничения на операции над рядами, например перестали заботиться о сходимости ряда. Использование рядов давало полезные результаты — и математики довольствовались практическим подтверждением правильности применяемых ими методов. Они далеко вышли за пределы того, что могли бы обосновать, но в целом обращались с расходящимися рядами довольно осторожно.

Хотя арифметика и алгебра были обоснованы ничуть не лучше математического анализа, математики сосредоточили свои усилия на последнем, надеясь изгнать из дифференциального и интегрального исчисления любую неоднозначность. Столь явное предпочтение математическому анализу объяснялось, несомненно, тем, что к началу XVIII в. различные типы чисел стали привычными и казались вполне естественными, в то время как понятия математического анализа по-прежнему оставались странными и даже загадочными, а потому менее приемлемыми. Кроме того, применение чисел не приводило к противоречиям, тогда как применение дифференциального и интегрального исчисления, бесконечных рядов и других разделов математического анализа рождало противоречия.

Ньютоновский подход к анализу потенциально легче поддавался обоснованию, чем подход Лейбница, хотя методология Лейбница отличалась большей гибкостью и была более удобной для приложений. Английские математики все еще надеялись обосновать оба подхода, связав их с евклидовой геометрией. К тому же они путали ньютоновские моменты (приращения неделимых, нынешние дифференциалы) и его непрерывные переменные. Математики, жившие в континентальной Европе, придерживались подхода Лейбница и пытались обосновать введенное им понятие дифференциала (бесконечно малой). Книги, посвященные объяснению и обоснованию подходов Ньютона и Лейбница, слишком многочисленны и противоречивы, чтобы подробно говорить о них.{78}

Пока одни математики предпринимали усилия, чтобы обосновать математический анализ, другие подвергали сомнению его правильность. Самым сильным нападкам математический анализ подвергся со стороны философа епископа Джорджа Беркли (1685-1753), опасавшегося, что вдохновляемая математикой философия механицизма и детерминизма создает растущую угрозу религии. В 1734 г. Беркли опубликовал сочинение под названием «Аналитик, или Рассуждение, адресованное одному неверующему математику [таковым он называл Эдмонда Галлея], в котором исследуется, являются ли предмет, принципы и заключения современного анализа более отчетливо познаваемыми и с большей очевидностью выводимыми, чем религиозные таинства и положения веры» [21]. «Вынь бревно из глаза своего, и ты узришь соринку в глазу брата своего». Беркли с полным основанием сетовал на загадочность и непонятность того, чем занимаются математики, поскольку те никак не обосновывали и не объясняли своих действий. Беркли подверг критике многие из рассуждений Ньютона, и в частности указал на то, что в «Рассуждении о квадратуре кривых» Ньютон (обозначавший приращение через x, а не h, как это сделали мы) выполнил несколько алгебраических операций, после чего отбросил члены, содержавшие h, мотивируя это тем, будто приращение h теперь обратилось в нуль. [Ср. равенства (3) и (4).] Поступая так, продолжал Беркли, Ньютон допустил вопиющее нарушение закона противоречия. Такого рода рассуждения в теологии были бы признаны неприемлемыми. Беркли утверждал, что первые флюксии (первые производные), по-видимому, выходят за рамки человеческого разумения, поскольку находятся за пределами конечного.

А если непостижимы первые [флюксии], то что можно сказать о вторых, третьих [производных от производных] и т.д.? Тот, кто сумеет постичь начало начал или конец концов… возможно, окажется достаточно проницательным, чтобы понять подобные вещи. Но, по моему глубокому убеждению, большинство людей не в состоянии понять их в каком бы то ни было смысле… Тому, кто сумеет превратить вторую и третью производную, думается, вряд ли стоит особо привередничать по поводу того или иного пункта в Священном писании.

Говоря об исчезновении (обращении в нуль) h и k, Беркли заметил: «Предполагая, что приращения исчезают, мы, несомненно, должны предположить, что их пропорции, выражения и все, вытекающее из их существования, исчезает вместе с ними». По поводу предложенного Ньютоном представления о производной как об отношении двух исчезающе малых величин h и k, Беркли высказался так: «Они не конечные величины, не величины бесконечно малые, не ничто. Как же не назвать их призраками покинувших нас величин?».

Столь же критически Беркли отнесся и к подходу Лейбница. На введенные Лейбницем понятия он обрушился еще в своей ранней работе «Трактат о принципах человеческого знания» (1710, переработанное издание — 1734) ([21], с. 149-248):

Некоторые из них, имеющие громкое имя, не довольствуются мнением, будто конечные линии могут быть делимы на бесконечное число частей, но утверждают далее, что каждая из этих бесконечно малых частей в свою очередь делима на бесконечное число других частей, или бесконечно малых величин второго порядка, и т.д. ad infinitum. Они утверждают, говорю я, что существуют бесконечно малые части бесконечно малых частей и т.д. без конца… Другие утверждают, что все порядки бесконечно малых величин ниже первого порядка суть ничто…

(([21], с. 234.))

Критику идей Лейбница Беркли продолжил в своем «Аналитике» [«Аналитик, или Рассуждение, адресованное неверующему математику» ([21], с. 395-442)]:

Лейбниц и его последователи в их calculus differentialis без тени сомнения сначала предполагают и затем отвергают бесконечно малые величины, что не может не заметить любой мыслящий человек, наделенный ясным умом и здравостью суждений и не относящийся к такого рода вещам с предвзятой благосклонностью,

Отношение дифференциалов, утверждал Беркли, геометрически должно означать тангенс угла наклона секущей, а не касательной. Эту ошибку математики совершают, пренебрегая высшими дифференциалами. Так, «благодаря двойной ошибке вы приходите хотя и не к науке, но все же к истине», потому что одна ошибка компенсирует другую. Неудовольствие Беркли вызвал и второй дифференциал Лейбница d(dx) — «разность величины dx, которая и сама едва различима».

«Можно ли назвать действия современных математиков, — спрашивал Беркли, имея в виду подход как Ньютона, так и Лейбница, действиями людей науки, если они с гораздо большим рвением стремятся применить свои принципы, нежели понять их?» «Во всякой другой науке, — утверждал Беркли, — люди доказывают правильность заключений, исходя из принятых ими принципов, а не принципы, исходя из заключений».

Беркли завершал свой «Аналитик» целой серией вопросов. Вот некоторые из них:

Разве математики, столь чувствительные в вопросах религии, столь же скрупулезно придирчивы в своей науке? Разве не полагаются они на авторитет, принимая многое на веру, и разве не веруют они в вещи, непостижимые для разума? Разве нет у них своих таинств и, более того, своих несовместимостей и противоречий?

Многие математики выступили с ответом на критику Беркли, и каждый из них пытался, но безуспешно, обосновать математический анализ. Наиболее значительную попытку предпринял Эйлер. Он полностью отверг геометрию как основу анализа и начал работать с функциями чисто формально, т.е. строить рассуждения, исходя из алгебраического (аналитического) представления функций. Эйлер отверг и предложенное Лейбницем понятие бесконечно малой как величины, которая меньше любого заданного числа, но все же не равна нулю. В своем сочинении «Основы дифференциального исчисления» (Institutiones calculi differentialis, 1755), классическом курсе математического анализа XVIII в., Эйлер привел следующее рассуждение:

Каждая величина, несомненно, может уменьшиться настолько, что исчезнет полностью и растает. Но бесконечно малая величина есть не что иное, как исчезающая величина, и поэтому сама равна нулю. Это полностью согласуется также с определением бесконечно малых величин, по которому эти величины должны быть меньше любого заданного числа. Ясно, что такая величина не может не быть нулем, ибо если бы она была отлична от нуля, то вопреки предположению не могла бы быть меньше самой себя.

Такие бесконечно малые, как dx (обозначение Лейбница), равны нулю, следовательно, равны нулю (dx)², (dx)³ и т.д., утверждал Эйлер, потому что последние принято считать бесконечно малыми более высокого порядка, чем dx. Производная dy/dx (в обозначениях Лейбница), бывшая для Лейбница отношением бесконечно малых, понимаемых в его смысле, для Эйлера, по существу, обращалась в неопределенность 0/0. Эйлер утверждал, что 0/0 может принимать много значений, так как n•0 = 0 при любом числе n, и, разделив равенство на 0, мы получим n = 0/0. Какое именно значение принимает 0/0 для вполне определенной функции, можно установить с помощью обычного метода вычисления производной. Эйлер демонстрирует это на примере функции y = x². Придадим переменной x приращение h (Эйлер обозначал приращение ?). Пока h, по предположению, не равно нулю. [Ср. сказанное в связи с выражениями (1) — (4).] Следовательно,

k/h = 2x + h.

Там, где Лейбниц считал приращение h бесконечно малым, но не равным нулю, Эйлер положил h равным нулю, после чего отношение k/h, т.е. 0/0, оказалось равным 2x.

Эйлер подчеркивал, что эти дифференциалы (предельные значения k и h) — абсолютные нули и из них нельзя извлечь ничего, кроме их отношения, которое и было вычислено в заключение и оказалось конечной величиной. В третьей главе «Основ анализа» Эйлера есть немало рассуждений такого рода. Стремясь приободрить читателя, Эйлер замечает, что понятие производной не столь уж загадочно, как обычно думают, хотя оно в глазах многих делает дифференциальное исчисление подозрительным. Разумеется, предложенное Эйлером обоснование метода нахождения производной было ничуть не более здравым, чем обоснования, предлагавшиеся Ньютоном и Лейбницем.

Формальный, некорректный подход Эйлера все же явился большим шагом вперед, ибо, избавляя математический анализ от традиционной основы — геометрии, подводил под него базу арифметики и алгебры. Этот шаг впоследствии привел к обоснованию анализа на основе понятия числа.

Наиболее претенциозная из последующих попыток заложить фундамент анализа была предпринята в XVIII в. Лагранжем. Подобно Беркли и другим своим предшественникам, Лагранж считал, что полученные с помощью анализа правильные результаты объясняются наложением и взаимной компенсацией ошибок. Свою собственную реконструкцию анализа Лагранж изложил в книге под названием «Теория аналитических функций» (1797; 2-е изд. — 1813).{79} Подзаголовок книги гласил: «Содержащая основные теоремы дифференциального исчисления, [доказанные] без использования бесконечно малых, исчезающих величин, пределов и флюксий, и сведенная к искусству алгебраического анализа конечных величин» (курсив М. К.).

Критикуя Ньютона, Лагранж, в частности, указывал, что, рассматривая предел отношения дуги к хорде, тот считал хорду и дугу равными не до и не после, а в момент исчезновения. В этой связи Лагранж заметил:

Такой метод чрезвычайно неудобен тем, что величины приходится рассматривать в тот самый момент, когда они, так сказать, перестают быть величинами, ибо, хотя мы всегда хорошо представляем отношения двух величин, покуда они остаются конечными, их отношение не дает уму никакого ясного и точного представления, коль скоро обе величины исчезают одновременно.

Лагранж не был удовлетворен ни бесконечно малыми величинами Лейбница, ни абсолютными нулями Эйлера, так как оба этих понятия, «хотя и правильны в действительности, все же недостаточно ясны для того, чтобы служить основанием науки, надежность выводов которой зиждется на ее очевидности».

Лагранж хотел придать математическому анализу всю строгость доказательств древних и стремился достичь желаемого путем сведения математического анализа к алгебре. В частности, Лагранж предложил использовать для строгого обоснования анализа бесконечные ряды, которые в то время было принято относить к алгебре, хотя с их обоснованием дело обстояло хуже, чем с обоснованием математического анализа. Лагранж «скромно» заметил, что его метод почему-то не пришел в голову Ньютону.

Нам нет необходимости вдаваться в подробности обоснования анализа «по Лагранжу». Помимо совершенно неудовлетворительного использования рядов Лагранж производил множество алгебраических преобразований, призванных скорее помешать читателю обнаружить немаловажное обстоятельство: отсутствие строгого определения производной. Все результаты, полученные Лагранжем, были обоснованы столь же плохо, как и результаты его предшественников. Лагранж был убежден, что ему удалось избавиться от понятия предела и построить весь анализ на основе алгебры. Несмотря на все допущенные Лагранжем ошибки, предложенный им вариант обоснования анализа имел несколько выдающихся продолжателей.

Мнение о том, что математический анализ представляет собой лишь продолжение алгебры, было подкреплено фундаментальным трехтомным трудом Сильвестра Франсуа Лакруа (1765-1843), вышедшим в 1797-1800 гг. Лакруа шел по стопам Лагранжа. В меньшей по объему однотомной работе под названием «Элементарный трактат по дифференциальному и интегральному исчислению» (1802) Лакруа использовал теорию пределов (точнее, то, что понимали под теорией пределов в начале XIX в.) — правда, по словам Лакруа, лишь для того, чтобы сэкономить место.

Некоторые английские математики начала XIX в. решили взять реванш над превосходившими их математиками из континентальной Европы. Чарлз Бэббедж (1792-1871), Джон Гершель (1792-1871) и Джордж Пикок (1791-1858), бывшие тогда выпускниками Кембриджского университета, основали Аналитическое общество и перевели краткий курс математического анализа Лакруа.{80} Однако в предисловии переводчиков говорилось следующее:

Сочинение Лакруа, перевод которого предлагается вниманию публики… может рассматриваться как сокращенный вариант его фундаментального труда по дифференциальному и интегральному исчислению, хотя при доказательстве первых принципов автор пользовался методом пределов Д'Аламбера вместо наиболее правильного и естественного метода Лагранжа, который он применил в более обширном своем сочинении…

Пикок утверждал, что теория пределов неприемлема, так как она отделяет принципы дифференциального исчисления от алгебры. Гершель и Бэббедж выразили полное согласие с мнением своего коллеги.

Насущная необходимость надлежащего обоснования математического анализа остро ощущалась в конце XVIII в. всем математическим миром, и по предложению Лагранжа отделение математики Берлинской академии наук, директором которой он состоял в 1766-1878 гг., назначила в 1784 г. приз (который должен был быть вручен в 1786 г.) за лучшее решение проблемы бесконечности в математике. Объявление об условиях конкурса гласило:

Своими предложениями, всеобщим уважением и почетным титулом образцовой «точной науки» математика обязана ясности своих принципов, строгости своих доказательств и точности своих теорем.

Для обеспечения непрестанного обновления столь ценных преимуществ этой изящной области знания необходима ясная и точная теория того, что называется в математике бесконечностью.

Хорошо известно, что современная геометрия [математика] систематически использует бесконечно большие и бесконечно малые величины. Однако геометры античности и даже древние аналитики всячески стремились избегать всего, что приближается к бесконечности, а некоторые знаменитые аналитики современности усматривают противоречивость в самом термине бесконечная величина.

Учитывая сказанное, Академия желает получить объяснение, каким образом столь многие правильные теоремы были выведены из противоречивого предположения, вместе с формулировкой точного, ясного, короче говоря, истинно математического принципа, который был бы пригоден для замены принципа бесконечного и в то же время не делал бы проводимые на его основе исследования чрезмерно сложными или длинными. Предмет должен быть рассмотрен во всей возможной общности и со всей возможной строгостью, ясностью и простотой.

К участию в конкурсе допускались все желающие, за исключением членов Академии, Всего на рассмотрение жюри поступило двадцать три работы. Официальное решение, опубликованное после окончания работы жюри, гласило:

Академия получила много работ на объявленную тему. Авторы всех работ не смогли объяснить, каким образом из противоречивого предположения — о существовании бесконечно большой величины — удалось вывести так много правильных теорем. Все авторы в большей или в меньшей степени пренебрегли требованиями ясности, простоты, а главное — строгости. Большинство из авторов даже не осознали, что принцип, который им надлежало найти, должен был не ограничиваться дифференциальным исчислением, а распространяться также на алгебру и геометрию, рассматриваемые в духе древних.

Учитывая изложенное, Академия считает, что ее требования удовлетворены не полностью.

Тем не менее жюри нашло, что в наибольшей мере удовлетворил требованиям участник конкурса, представивший работу на французском языке под девизом «Бесконечность — пучина, в которой тонут наши мысли». Ему и присужден приз.

Победителем оказался швейцарский математик Симон Люилье. В том же 1876 г. Берлинская академия опубликовала его «Элементарное изложение высшего анализа». Несомненно, решение, принятое математическим отделением Академии, по существу было правильным. Ни в одной из других работ (за исключением работы, представленной Карно; см. гл. VII) даже не делалось попытки объяснить, каким образом в математическом анализе исходя из ложных посылок удается вывести так много правильных теорем. Люилье, несомненно, заслуживал награды, хотя основная идея его работы была далеко не оригинальна. По словам самого Люилье, его работа представляла «развитие идей… бегло намеченных Д'Аламбером и как бы изложенных в его статье «Дифференциал», опубликованной в «Энциклопедии», и в его сочинении «Разное». Во вводной главе своего сочинения Люилье излагает слегка усовершенствованный вариант теории пределов. Впервые в печатном тексте он ввел для обозначения предела символ lim. Производную dP/dx (ранее встречавшуюся как отношение k/h) Люилье обозначал lim ?P/?x, но вклад самого Люилье в теорию пределов был крайне незначительным.

Хотя почти каждый математик XVIII в. предпринимал попытку обосновать математический анализ или по крайней мере высказывал свое мнение по поводу столь важной проблемы, а два-три математика были на верном пути, все усилия оказались тщетными. Математики XVIII в. либо умышленно обходили все сколько-нибудь важные и тонкие проблемы, либо просто не замечали их. Различие между очень большим числом и бесконечно большой величиной они ощущали с трудом. Математикам XVIII в. казалось очевидным, что теорема, которая выполняется при любом конечном n, должна выполняться и при бесконечном n. Разностное отношение k/h [см. выражение (3)] они охотно заменяли производной, а сумму членов вида (7) с трудом отличали от интеграла. Переход от конечного к бесконечному как в одну, так и в другую сторону совершался ими необыкновенно легко и просто. Суть математики XVIII в., пожалуй, наиболее точно выразил Вольтер, охарактеризовавший [математический] анализ как «искусство считать и точно измерять то, существование чего непостижимо для разума». Предпринимавшиеся на протяжении века попытки строгого обоснования анализа, в особенности попытки, предпринятые такими гигантами науки, как Эйлер и Лагранж, лишь окончательно запутали и завели в тупик как их современников, так и математиков последующих поколений. В целом подобные попытки оказались безнадежно ошибочными — от них можно было бы прийти в отчаяние и усомниться в том, что математикам вообще когда-нибудь удастся разрешить проблему обоснования анализа.

Математики верили в символы больше, чем в логику. Поскольку бесконечный ряд имеет один и тот же вид при всех значениях x, различие между значениями x, при которых ряд сходится, и теми значениями, при которых он расходится, не привлекало должного внимания. И хотя было известно, что некоторые ряды, например 1 + 2 + 3 + …, имеют бесконечную сумму, математики предпочитали пытаться придать какой-то смысл бесконечной сумме, чем усомниться в применимости суммирования. Было бы неверно утверждать, что математики XVIII в. не ощущали необходимости доказательства некоторых утверждений. Мы видели, что Эйлер пытался обосновать использование расходящихся рядов. Более того, Эйлер, Лагранж и многие другие математики пытались обосновать математический анализ. Но немногочисленные попытки достичь желаемой строгости (ценные тем, что они показали, как изменяются со временем критерии математической строгости) не увенчались успехом. Математический анализ, созданный трудом многих людей на протяжении почти столетия, по-прежнему оставался под сомнением. И математики, можно сказать, сознательно прибегли к житейской мудрости: если анализ нельзя излечить, необходимо хотя бы продлить ему жизнь. В своих рассуждениях мыслители XVIII в. нередко обращались к термину «метафизика». Под ним понимали совокупность истин, лежащих за пределами собственно математики. В случае необходимости эти истины могли быть использованы для обоснования того или иного математического утверждения, хотя природа метафизических истин оставалась неясной. Обращение к метафизике означало использование аргументов, которые не подкреплялись разумом. Так, Лейбниц утверждал, что метафизика используется в математике шире, чем можно себе представить. Единственным «обоснованием» равенства ¹/₂ = 1 ? 1 + 1 ? 1 + 1 ? … и принципа непрерывности было утверждение Лейбница о том, что оба утверждения «обоснованы» метафизически. Предмет спора исчезал, коль скоро появлялось метафизическое «обоснование». Эйлер также обращался к метафизике и доказывал, что метафизические аргументы должны приниматься в анализе на веру. Всякий раз, когда математики XVII-XVIII вв. не находили подобающего аргумента в подтверждение того или иного утверждения, они говорили, что это утверждение верно по метафизическим причинам.

Итак, XVIII в. закончился, оставив обоснование дифференциального и интегрального исчисления и высших разделов математического анализа в крайне неудовлетворительном состоянии. Без преувеличения можно было сказать, что к началу XIX в. ситуация с обоснованием математического анализа выглядела гораздо хуже, чем в канун XVIII в. Гиганты науки, главным образом Эйлер и Лагранж, дали неверные обоснования анализа. А поскольку их авторитет был чрезвычайно велик, многие из их коллег воспринимали и некритически повторяли все, что делали корифеи, и даже пытались строить новые теории на возведенных теми ложных основаниях. Другие, менее доверчивые, не были удовлетворены тем, что предлагали Эйлер и Лагранж, но надеялись достичь полного обоснования путем незначительных поправок и дополнений. Нужно ли говорить, что и они стояли на неверном пути.

Примечания:

7

С этой точки зрения характерно, что Предложение 1 евклидовых «Начал» содержит построение равностороннего треугольника, что единственно оправдывает данное несколько ранее определение такого треугольника (ср. [25], с. 13, 15-16).

8

Так, например, еще Платон весьма высоко ценил логический метод «доказательства от противного», при котором установление истинности предложения p начинается с предпосылки «пусть p неверно», и из этой предпосылки выводится противоречие [так, пифагорейское доказательство иррациональности v2 (в наших обозначениях) начинается с утверждения: «Пусть v2 = m/n — рационально…»]. Общую форму этому методу придал, как будто, основатель так называемой элейской школы в древнегреческой философии Парменид (V в. до н.э.), глубоко почитавшийся Платоном (ему посвящен диалог Платона «Парменид»).

76

Недворянин Жиль Персон называл себя «де Роберваль» по названию деревни, из которой он был родом, и вошел в историю науки именно под последним именем.

77

Идущее от Ферма понятие дифференциала функции, равно как и утверждение о том, что в точках максимума или минимума функции ее дифференциал (а, значит, и производная) обращается в нуль (это утверждение сегодня часто называют теоремой Ферма), были даны им лишь для конкретных примеров функций.

78

Обзор этих работ см. в кн.: Cajori F. A History of the Conceptions of Limits and Fluxions in Great Britain from Newton to Woodhouse. — Chicago: The Open Court Publishing Co., 1915. См. кроме того: Boyer С. The Concepts of the Calculus. — N.Y.: Columbia University Press, 1939, а также (переиздание): Dover Publications, 1949. [Из более поздних работ можно указать, например, брошюру [40] и более обстоятельные книги [41], [42], [43] и особенно [44] — Прим. ред.]

79

В этой книге излагался курс, который Лагранж читал студентам знаменитой парижской Политехнической школы; продолжение и дальнейшее развитие идей Лагранжа содержат учебники еще одного профессора Политехнической школы — О. Коши, о которых пойдет речь в следующей главе.

80

Деятельность молодых кембриджских математиков (Пикок — Бэббедж — Гершель) имела еще один аспект, не связанный с проблемами обоснования математики, но чрезвычайно важный в тот период для английской науки. Дело в том, что крайне неприятные приоритетные споры об открытии математического анализа, развернувшиеся в XVII в. между Ньютоном и Лейбницем, формально окончилась  как будто бы полной победой Ньютона, не потерпевшего в результате их ни малейшего материального или морального ущерба, тогда как Лейбниц из-за этих споров умер буквально в нищете. Однако исторически победителем здесь оказался именно Лейбниц, а научным наследникам Ньютона эти беспредметные дискуссии о первенстве принесли вполне ощутимый вред. Вся континентальная Европа восприняла дифференциальное и интегральное исчисление в том обличье, которое ему придал Лейбниц — с более удобной лейбницевской символикой и терминологией (производная и интеграл, а не флюксия и флюэнта; исчисление дифференциалов, а не моментов). Существенную роль здесь сыграла отмеченная в книге темпераментная защита Лейбницем своих позиций, а также выдающаяся научная школа Лейбница, возглавляемая братьями Якобом и Иоганном Бернулли. Напротив, в Англии из-за приоритетных соображений на систему обозначений и терминов Лейбница был буквально наложен запрет, что лишало возможности молодых английских ученых следить за достижениями своих континентальных коллег и привело к резкому отставанию английской науки. Даже возрождение английской математики в середине XIX столетия (!), предвестником которого явились названные молодые кембриджцы, было первоначально встречено на континенте с большим недоверием. И деятельность Пикока и его друзей, в частности перевод ими на английский язык «лейбницианского» по форме учебника Лакруа, ставила своей целью приблизить английскую математику к континентальной.