Наука: Проблемы 2000 года: гипотеза Римана

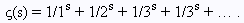Любой студент, прослушавший курс математического анализа, тут же скажет, что этот ряд сходится для всякого вещественного s > 1. Более того, он сходится и для комплексных чисел, вещественная часть которых больше единицы. Еще более того, функция ?(s) — аналитическая в этой полуплоскости.

Рассматривать формулу для отрицательных s кажется дурной шуткой: ну какой смысл складывать, например, все положительные целые числа или, тем более, их квадраты или кубы? Однако комплексный анализ — упрямая наука, и свойства дзета-функции таковы, что ее можно продолжить на всю плоскость. Это и было одной из идей Римана, изложенных в мемуаре 1859 года. У полученной функции только одна особая точка (полюс): s = 1, а, например, в отрицательных вещественных точках функция вполне определена. Именно значение аналитически продолженной дзета-функции в точке —1 и выражает формула, с которой я начал этот раздел.

(Специально для патриотов и неравнодушных к истории науки людей отмечу в скобках, что, хотя мемуар Бернарда Римана внес в теорию чисел много свежих идей, он не был первым исследованием, в котором распределение простых чисел изучалось аналитическими методами. Впервые это сделал наш соотечественник Пафнутий Львович Чебышёв, 24 мая 1848 года прочитавший в петербургской Академии наук доклад, в котором изложил ставшие классическими асимптотические оценки количества простых чисел.)

Но вернемся к Риману. Ему удалось показать, что распределение простых чисел — а это центральная проблема теории чисел — зависит от того, где дзета-функция обращается в нуль. У нее есть так называемые тривиальные нули — в четных отрицательных числах (—2, —4, —6, …). Задача состоит в том, чтобы описать все остальные нули дзета-функции.

Этот орешек вот уже полторы сотни лет не могут разгрызть самые талантливейшие математики планеты.

Правда, мало кто сомневается в том, что гипотеза Римана верна. Во-первых, численные эксперименты более чем убедительны; о последнем из них рассказывает статья Хавьера Гурдона (Xavier Gourdon), название которой говорит само за себя: «Первые 10 13 (10 в 13-ой) нулей дзета-функции Римана и вычисление нулей на очень большой высоте» (вторая часть названия означает, что предложен метод вычисления не только первых нулей, но и некоторых, пусть и не всех, более далеких, вплоть до нулей с номером около 10 24 (10 в 24-ой)). Эта работа пока венчает более чем столетнюю историю попыток проверки гипотезы Римана для некоторого количества первых нулей. Разумеется, контрпримеров к гипотезе Римана не найдено. Кроме того, строго установлено, что больше 40% нулей дзета-функции гипотезе удовлетворяют.

Второй аргумент напоминает одно из доказательств существования Бога, опровергнутых еще Иммануилом Кантом. Если Риман все же ошибся, то неверной станет очень много красивой и правдоподобной математики, построенной в предположении, что гипотеза Римана правильна. Да, этот аргумент не имеет научного веса, но все же… математика — это наука, где красота играет ключевую роль. Красивое, но неверное доказательство сплошь и рядом оказывается полезнее, чем верное, но некрасивое. Так, например, из неудачных попыток доказать великую теорему Ферма выросло не одно направление современной алгебры. И еще одно эстетическое замечание: теорема, аналогичная гипотезе Римана, была доказана в алгебраической геометрии. Получившаяся теорема Делиня (Deligne) по праву считается одним из самых сложных, красивых и важных результатов математики XX столетия.

Итак, гипотеза Римана, по всей видимости, верна — но не доказана. Кто знает, возможно, сейчас этот журнал читает человек, которому суждено войти в историю математики, доказав гипотезу Римана. В любом случае, как и со всеми остальными великими задачами, сразу предупреждаю: не пытайтесь повторить эти трюки дома. Иными словами, не пытайтесь решать великие проблемы, не поняв теории, которая их окружает. Сэкономите нервы и себе, и окружающим.

На десерт — еще немного интересного о дзета-функции. Оказывается, у нее есть и практические применения, и даже физический смысл. Более того, и гипотеза Римана (точнее говоря, ее обобщение, считающееся столь же сложным, сколь и она сама) имеет прямые практические следствия. Например, одной из важных вычислительных задач является проверка чисел на простоту (дано число, нужно сказать, простое оно или нет). Самый теоретически быстрый на данный момент алгоритм решения этой задачи — тест Миллера-Рабина (Miller-Rabin test) — работает за время O(log n), где n — данное число (соответственно log n — длина входа алгоритма). Однако доказательство того, что он работает так быстро, опирается на гипотезу Римана.

Впрочем, тест на простоту — не слишком сложная проблема с точки зрения теории сложности (в 2002 году был разработан не зависящий от гипотезы Римана алгоритм, который медленнее теста Миллера-Рабина, но тоже полиномиален). Раскладывать числа на простые сомножители гораздо интереснее (и прямые криптографические приложения налицо — стойкость схемы RSA зависит от того, можно ли быстро разложить число на простые), и здесь гипотеза Римана тоже является необходимым условием для доказательства оценок времени работы некоторых быстрых алгоритмов.

Обратимся к физике. В 1948 году голландский ученый Хендрик Казимир (Hendrik Casimir) предсказал эффект, носящий теперь его имя[Эффект Казимира долгое время оставался лишь изящной теоретической идеей; однако в 1997 году Стив Ламоро (Steve K. Lamoreaux), Умар Мохидин (Umar Mohideen) и Анушри Руа (Anushri Roy) смогли провести подтверждающие предшествующую теорию эксперименты]. Оказывается, если сблизить две незаряженные металлические пластины на расстояние в несколько атомных диаметров, они притянутся друг к другу за счет флуктуаций расположенного между ними вакуума — постоянно рождающихся пар частиц и античастиц. Этот эффект чем-то напоминает притяжение подплывших слишком близко друг к другу судов в океане (еще больше он напоминает теорию Стивена Хокинга [Stephen Hawking] о том, что черные дыры все же излучают энергию, — впрочем, тут трудно сказать, кто кого напоминает). Расчеты физической модели этого процесса показывают, что сила, с которой притягиваются пластины, должна быть пропорциональна сумме частот стоячих волн, возникающих между пластинами. Вы уже догадались — эта сумма сводится к сумме 1+2+3+4+…. И более того — правильным значением этой суммы для расчетов эффекта Казимира является именно —1/12.

Но и это еще не все. Некоторые исследователи считают, что дзета-функция играет важную роль… в музыке! Возможно[Я пишу «возможно», потому что единственный источник, который мне удалось разыскать, это переписка в usenet-конференции sci.math. Если вы (читатели) сможете найти более авторитетные источники, мне будет очень интересно об этом услышать], максимумы дзета-функции соответствуют значениям частот, которые могут служить хорошей основой для построения музыкальной шкалы (такой, как наш нотный стан). Что ж, Герман Гессе в своей «Игре в бисер» не зря объявил Игру комбинацией математики и музыки: между ними и впрямь много общего…