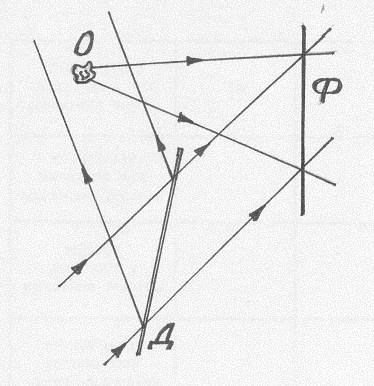
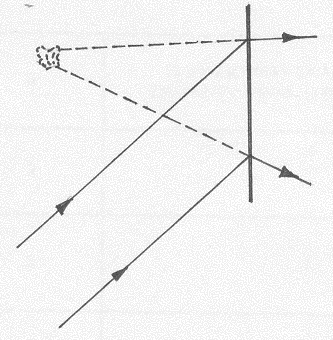
Некоторые древнегреческие философы учили, что мы видим глазами потому, что из глаз выходят тончайшие щупальца, которыми мы ощупываем предметы на расстоянии. Эта концепция, в рамках тогдашних знаний о мире, выглядела вполне правдоподобно. А рухнула она от простенького возражения – попробуйте, мол, что-нибудь вот так ощупать в совершенно тёмной комнате! Не получается? То-то же. Пришлось допустить, что мы можем видеть глазами предметы тогда, когда в глаза попадает нечто, идущее от предметов. Это нечто и есть свет. В тёмной комнате света нет, поэтому там – «хоть глаз выколи».

История развития научных представлений о природе света – это история углубления научного бессилия. Ибо чем больше появлялось опытных данных про свет, тем становилось всё яснее, что научные представления о нём – никуда не годные.

Ньютон представлял свет как поток корпускул. Первые же измерения скорости света показали, что световые корпускулы должны летать с огромной скоростью. Представляете, как они сталкивались бы при пересечениях курсов, и как при этом они изменяли бы направления полёта! Однако, лучи зрения множества наблюдателей могут пересекаться, и при этом каждый наблюдатель успешно видит свой объект. Такое может быть, по Ломоносову, если свет – это не поток корпускул, а волны в какой-то особой среде. Ведь для волн как раз характерно – проходить друг сквозь друга без взаимных помех! Но лишь когда у света обнаружились дифракция и интерференция – лишь тогда волновая теория стала господствующей. Пришлось придумать среду – световой эфир – где распространявшиеся механические колебания и представляли собой световые волны. Ох, и намучились физики, пытаясь построить модель эфира. Ведь эфир должен был обеспечивать механические колебания на оптических частотах, которые распространялись бы с огромной скоростью – скоростью света! Для механических колебательных систем эти цифры – совершенно запредельные. Хуже того: уравнения Максвелла, которые изначально описывали механические колебания в эфире – и давали, в качестве решения, распространяющиеся волны – были, по сути, уравнениями сплошной среды. Однако, сплошных сред в природе не бывает, да и механические колебания возможны в тех средах, которые состоят из отдельных частичек, связанных силами упругости. Но самые большие трудности из-за концепции эфира возникли в оптике движущихся тел. Считалось, что эфир заполняет всё мировое пространство, будучи однороден, изотропен и неподвижен. А скорость упругих волн в среде определяется только свойствами этой среды, поэтому волна движется с характеристической скоростью по отношению к местному участку среды. Казалось бы, экспериментатор на Земле, вектор скорости которой по отношению к эфиру изменяется (из-за годичного обращения), мог бы обнаружить соответствующие вариации скорости света. Но, увы… Были предложены модели, в которых эфир движущимися телами увлекался – частично или полностью. Всё тщетно. Ни одна модель эфира не объясняла всей совокупности экспериментальных фактов. Наконец, с подачи Эйнштейна, эфир упразднили. Но уравнения Максвелла сохранили, поскольку на их лорентц-инвариантности и держалось всё то, что называлось «теорией относительности». Раньше уравнения Максвелла описывали волны в среде, а теперь они стали «описывать» волны в чистом поле, без всякой среды. Откуда там, в чистом поле, берутся возвращающие силы, необходимые для наличия и распространения колебаний (кстати, колебаний чего?) – науке это до сих пор не ведомо. Причём, когда это всё начиналось, было уже хорошо известно, что характеристические спектры атомов представляют собой наборы отдельных линий. Считалось, что каждой такой линии соответствует своя волна, которая излучается при механических осцилляциях электрона в атоме – на резонансной частоте.

И вот произошли два свершения. Второе из них: Резерфорд предложил планетарную модель атома. Основания для этой модели были, но, согласно ей, электроны в атоме осциллировали постоянно, поскольку они обращались вокруг ядра. А, значит, постоянно порождали световые волны. А, значит, постоянно теряли энергию. И, стремительно падая по спирали на ядро, успевали бы излучить широченный спектр – вместо отдельных линий, наблюдавшихся на опыте… А, несколько ранее этого свершения, Планку удалось соорудить математическое выражение, описывавшее спектр равновесного излучения, у которого максимум при комнатной температуре находится в инфракрасной области. Тут, правда, не обошлось без надувательства. Смотрите: выражение для электромагнитного спектра можно записать так, чтобы аргументом являлась частота – а можно так, чтобы аргументом являлась длина волны. Планк предложил оба эти варианта [П1,П2]. Казалось бы, это два выражения для одного и того же спектра. Но, поразительным образом, их максимумы сильно не совпадают. Чтобы в этом убедиться, следует взять производные от этих выражений и, приравняв их нулю, найти положения максимумов, а затем привести результаты к какой-нибудь одной физической величине – например, к энергии, удачно выражаемой в единицах kT, где k - постоянная Больцмана, а T - абсолютная температура. И окажется, что максимум длин-волнового выражения Планка соответствует энергии 4.97kT, а максимум частотного выражения Планка – энергии 2.82kT [Г1]. Не мы первые это обнаружили: вопрос обсуждался даже на академическом уровне [Г2,С1,Г3]. Авторы предлагали «промежуточный» вариант выражения для равновесного спектра – с однозначным максимумом. Но, увы, этот вариант не находился в согласии с опытом: на опыте блестяще подтверждалось длин-волновое выражение Планка [Б1,Л1]. А в чём же тогда было надувательство? А в том, что всю квантовую теорию, со всеми её далеко идущими следствиями, строили на частотном выражении Планка, которое на опыте не подтверждалось!

И вот, в этом выражении, не подтверждаемом на опыте, фигурировало произведение частоты на подгоночный множитель, которому впоследствии присвоили статус фундаментальной константы – постоянной Планка. Произведение конкретной частоты на эту постоянную давало конкретную порцию энергии. Вот же они, кванты света! Ух, как они пригодились, чтобы решить проблему с устойчивостью атомов, которая возникала в планетарной модели Резерфорда! Бор, не напрягаясь, всё разъяснил: у атомарного электрона, мол, есть набор стационарных орбит, по которым он обращается, не излучая. А излучение-поглощение – квантами! – происходит, мол, при переходах с одной стационарной орбиты на другую. Эти переходы, мол, и дают наблюдаемые линейчатые спектры! Всё хорошо, но почему электрон, обращаясь по стационарной орбите, не излучает? Да, получается, потому, что Бор так постулировал!

Знаете, зависимость энергии кванта света только от частоты – это поначалу людей с ума сводило. Ведь квант света представляли как отрезочек электромагнитной волны. Сколько же периодов колебаний укладывается на этом отрезочке? Казалось бы: вдвое больше число колебаний – вдвое больше и энергия. Ан нет, при одной и той же частоте, квант длиной в одно колебание и квант длиной в миллион колебаний должны иметь одинаковую энергию! И, если частота является единственным параметром, определяющим энергию кванта, то что колеблется с этой частотой в атоме, поглотившем этот квант? И сколько длится «акт испускания» кванта атомом, тот самый переход электрона с орбиты на орбиту? Отчаявшись найти разумные ответы на эти вопросы, физики на Первом Сольвеевском конгрессе приняли постановление о том, что квант излучается и поглощается мгновенно. Так оно, конечно, спокойнее – если забыть про то, что этот «отрезочек волны» движется со скоростью света, и что он должен иметь какую-никакую длину. Ведь этот вопрос – насчёт длины кванта – на редкость мутный. Вот, например, фемтосекундный лазер. Длина светового импульса длительностью 100 фемтосекунд – 30 микрон. А вот другой пример – узкополосный лазер на красителе фирмы «Coherent Radiation». При ширине его спектра всего в 15 кГц, эквивалентная длина когерентности составляет 3 км. Какова же длина кванта света, если она – то не более 30 микрон, то не менее 3 км? Кстати, если квант света имел бы длину 30 микрон, то как он мог бы лететь в прозрачном твёрдом теле от атома к атому, если расстояние между ними составляет несколько Ангстрем? Вы, дорогой читатель, представляете, как от атома к атому может лететь нечто, имеющее длину на пять порядков больше, чем расстояние между ними? Не получается? Ну, ладно, тогда про 3-километровый квант лучше и не вспоминать…

Впрочем, это всё можно назвать лёгкими недоразумениями по сравнению с центральным догматом квантовой теории – согласно которому, атом может поглощать и излучать только такие кванты света, энергии которых в точности равны разностям энергий атомарного электрона на тех самых стационарных орбитах. Как такое можно было сморозить? Ведь у атомов различных химических элементов различны и наборы квантовых уровней энергии, соответствующих «стационарным орбитам». Выходит, что без специальных мер – сдвигающих или уширяющих квантовые уровни – квант света, излучённый атомом одного элемента, не может быть поглощён атомом другого элемента. Позвольте, если бы так оно и было, то электромагнитное взаимодействие не было бы универсальным! Вот эти атомы обменивались бы только такими квантами, а вон те – другими! Но, к счастью, таких глупостей в мироустройстве нет – известно множество свидетельств о том, что атомы способны поглощать и излучать не только резонансные световые кванты, соответствующие разностям энергий квантовых уровней в атоме, но и нерезонансные кванты, соответствующие континууму между квантовыми уровнями. Первое из этих свидетельств было известно с самого рождения квантовой теории – это спектр равновесного излучения, который, как известно, сплошной. А нам пытаются вдолбить, что атом может поглотить-излучить лишь дискретные порции энергии! Если бы это было так, то атомы не могли бы быть источниками равновесного излучения – а, значит, не могли бы участвовать в равновесном радиационном теплообмене! Но это вопиющее противоречие квантовой теории с тем, чему нас учит термодинамика, не образумило теоретиков – они, наверное, думали, что со временем это всё забудется, и тогда придёт полное понимание. Отнюдь: со временем появились ещё и экспериментальные опровержения центрального догмата квантовой теории. Например, вопреки квантовой теории, заработали лазеры. В первых лазерах использовалась накачка импульсными широкополосными лампами-вспышками. Атомы рабочего тела поглощали нерезонансные кванты накачки, после чего скатывались на верхний уровень лазерного перехода. Известно, далее, о флуоресценции веществ в результате их облучения заведомо нерезонансным ультрафиолетом: она происходит на длине волны, в точности соответствующей разности энергий нерезонансного кванта облучения и энергии нижерасположенного квантового уровня в облучаемом веществе. Наконец, в современной лазерной спектроскопии активно развиваются направления, в которых поглощение-излучение атомами нерезонансных квантов рассматривается уже как нечто само собой разумеющееся. Речь идёт о генерации суммарной частоты, а также о разнообразных методиках многофотонной спектроскопии (см. обзорную монографию [Д1]). В физическом жаргоне появился термин «виртуальный уровень» – это на нём, на виртуальном уровне, оказывается атом при поглощении нерезонансного кванта (к вопросу о континууме энергий между стационарными уровнями мы вернёмся в 5.1). Но, несмотря на перечисленные потрясающие успехи экспериментаторов, никто официально не отменил запрета квантовой теории на поглощение-излучение атомами нерезонансных квантов.

А почему так? А потому что тронь центральный догмат квантовой теории – и вся эта гнилая конструкция рухнет, ибо она изначально строилась не неверных предпосылках. Главной из этих неверных предпосылок является тезис о том, что кванты света – или, как их стали называть впоследствии, фотоны – являются порциями энергии, которые существуют самостоятельно, независимо от атомов, которые их излучают и поглощают. Однако, по логике «цифрового мира», обладателем физических энергий, в самых различных формах, является только вещество (1.1). Световая энергия не является исключением: она тоже локализована только на атомах. При распространении света она не проходит по разделяющему атомы пространству: энергия возбуждения перебрасывается – на расстояние! – непосредственно с атома на атом. О квантовых перебросах этой энергии мы будем подробно говорить ниже (3.4). Как нам представляется, все попытки физиков построить сколько-нибудь разумную и непротиворечивую модель фотона провалились по одной простой причине: никаких фотонов, в традиционном понимании, не существует. А ведь фотон, как считается, входит в четвёрку фундаментальных, абсолютно стабильных частиц! Но мы покажем, что потуги выдать фотон за реальную частицу – через приписывание фотону свойств реальных частиц – являлись либо заведомой ложью, либо неверной интерпретацией опытных фактов. И вначале мы разберёмся – чего стоят «доказательства» того, что фотоны переносят импульс.

Первым и весьма наглядным свидетельством о том, что световая энергия передаётся порциями, стало явление фотоэффекта – вылета электронов из металлической пластинки, облучаемой ультрафиолетом. Если бы энергия облучения падала на пластинку «волнами», то энергии фотоэлектронов увеличивались бы по мере увеличения интенсивности облучения. Однако, энергии фотоэлектронов увеличивались лишь по мере уменьшения длины волны облучения. «Это потому, - разъяснил Эйнштейн, - что каждый фотоэлектрон выбивается одним квантом света, энергия которого и превращается в кинетическую энергию электрона – за вычетом потери на работу выхода из пластинки». Впрочем, «выбивается» - это сильно сказано. Фотоэлектроны вылетали из освещённой стороны пластинки – словно их только припекло, но не пнуло! Они вылетали в направлении, противоположном направлению полёта «выбивавших» их квантов света! Как это получалось, даже Эйнштейн объяснить не брался. О законе сохранения энергии здесь можно было говорить уверенно, а вот о законе сохранения импульса… Ну, да чёрт с ним. Для Нобелевской премии и этого хватило!

А уж как хотелось получить свидетельства о том, что кванты света переносят не только энергию, но и импульс! Вон, чем ближе комета к Солнцу, тем сильнее её ядро «пылит и газит», и тем сильнее это пыле-газовое облако (кома) «сметается» в направлении от Солнца – отчего у кометы формируется хвост. Считается, что Кеплер первый высказал в 1619 г. гипотезу о том, что «сметающим» фактором, формирующим хвосты комет, является давление светового излучения Солнца. Впоследствии электромагнитная теория света Максвелла привела к выводу о том, что давление света прямо пропорционально световой энергии, ортогонально падающей на площадку в единицу времени. Например, для давления, оказываемого солнечными лучами на радиусе орбиты Земли, на основе величины солнечной постоянной, ?1400 Вт/м², получается величина около 5?10^-6 н/м². Лебедев утверждал [Л2], что именно давление солнечного света формирует хвосты комет, но соответствующих расчётов он не привёл – для таких расчётов требовалось знать множество параметров пыле-газовых облаков комет, а этими знаниями наука тогда не располагала.

Сегодня, когда наука такими знаниями располагает, всё так же необоснованно считается, что давление солнечного света является основным фактором, формирующим хвосты комет. Между тем, сегодня известно о потоке плазмы от Солнца – солнечном ветре – частицы которого, несомненно, переносят импульс. При средних значениях параметров солнечного ветра на радиусе орбиты Земли, т.е. при концентрации частиц, равной 10 протонам в 1 см³, и их скоростях, равных 500 км/c [Ф1], для давления солнечного ветра получаем величину ?4.3?10^-9 н/м². Это на три порядка меньше величины светового давления, полученной на основе солнечной постоянной (см. выше) – и, казалось бы, говорить о действии солнечного ветра применительно к хвостам комет неуместно, поскольку здесь световое давление явно доминирует. Однако, такой подход не учитывает одно важное обстоятельство. А именно: солнечная постоянная характеризует излучение в широком сплошном спектре. Молекулы же газов, из которых состоит кома кометы, рассеивают лишь то излучение (в видимом диапазоне), которое попадает на полосы поглощения. Если учесть этот селектирующий фактор, то доминирующим оказывается действие солнечного ветра [Г4]. Причём, вопрос о том, какое из двух давлений – солнечного света или солнечного ветра – формирует хвосты комет, без особых проблем мог быть разрешён астрономическими наблюдениями. Известно, что в годы активного Солнца солнечный световой поток, практически, постоянен, а вот интенсивность солнечного ветра возрастает на порядок. Значит, если хвосты комет формируются давлением солнечного света, то заметной разницы у хвостов комет при спокойном и активном Солнце не наблюдалось бы, а если они формируются давлением солнечного ветра – разница наблюдалась бы. О недостатке объектов для наблюдения говорить не приходится: «Ежегодно наблюдается около десятка комет. Из них… 4-5 наблюдавшихся ранее, причём об их повторном появлении известно заранее. Две кометы – Швассмана-Вахмана и Отерма – наблюдаются ежегодно» [С2]. Тем не менее, нам удалось найти лишь одно свидетельство по данному вопросу: «Немецкий астроном Бирманн недавно выдвинул предположение, что солнечное корпускулярное излучение, т.е. частицы, вылетающие из Солнца с большими скоростями, тоже могут играть важную роль; он нашёл подтверждение своей теории в изучении влияния солнечных магнитных бурь на комету Уиппла-Федтке» [С3]. Одного этого свидетельства достаточно для вывода о том, что хвосты комет формируются, главным образом, под действием солнечного ветра – и, таким образом, хвосты комет не могут служить доказательством наличия светового давления.

А обнаруживается ли давление света в лаборатории? Считается, что оно обнаружилось в опытах Лебедева [Л3]. В этих опытах свет от электрической дуги направлялся на мишени из фольги, прикреплённые к крылышкам лёгких крутильных маятников разных конструкций. За время освещения с одной стороны, маятнику давали совершить одно полное колебание, замечая при этом три положения максимальных отклонений – по которым вычисляли нулевое положение. Затем свет направляли с другой стороны, и точно так же находили новое нулевое положение. Половина разности между этими двумя нулевыми положениями, как полагали, соответствовала силовому эффекту от светового давления.

Но главным фактором, маскировавшим искомый эффект, являлись радиометрические силы [Л3]. Эти силы обусловлены тем, что, в прилегающем к мишени объёме, температура газа с освещённой стороны выше, чем с неосвещённой – что порождает соответствующую разницу давлений на мишень. Радиометрические силы в значительной степени ослаблялись вакуумированием баллона, в котором помещался крутильный маятник; но полностью эти силы, конечно, не устранялись. Вызывает недоумение тот факт, что величину ожидаемого эффекта из-за действия этих сил – для реальных условий опыта – автор не привёл. Тогда не могло ли оказаться, что этими силами был обусловлен весь наблюдаемый эффект?

В пользу этого подозрения мы усматриваем одно важное свидетельство. Согласно теории Максвелла, давление света зависит от коэффициента отражения поверхности, на которую падает свет: для абсолютно отражающей поверхности давление в два раза больше, чем для абсолютно поглощающей. Поэтому Лебедев и использовал два типа мишеней: сильно поглощающих, покрытых платиновой чернью – и сильно отражающих, имевших зеркальное напыление. Но, вместо ожидавшейся почти двукратной разницы, имело место лишь незначительное превышение наблюдаемого эффекта для зеркальных мишеней по сравнению с чернёными. На основе рядов данных в [Л3], которые имеет смысл сравнивать, т.е. полученных для одного и того же маятника и одного и того же калориметра, измерявшего падавшую энергию, мы получили следующие средние величины эффекта (в условных единицах):

маятник N2 – (чернь) 1.55±0.07, (зеркала) 1.89±0.31;

маятник N3 – (чернь) 1.30±0.18, (зеркала) 1.70±0.24.

Как можно видеть, для маятника N2 отношение средних величин эффектов для чернённых и зеркальных мишеней составило всего-то 1.2, а для маятника N3 – 1.3. Эти цифры говорят о том, что Лебедев имел дело не с давлением света, а, скорее всего, с остаточными радиометрическими силами.

Весьма показательно и следующее обстоятельство. Спустя десятилетия, опыты Лебедева могли быть повторены в условиях, гораздо более благоприятных для устранения радиометрических сил. В баллоне Лебедева давление остаточных газов было несколько ниже, чем 10^-4 мм.рт.ст. [Л3]. Для сравнения: при поточном производстве радиоламп, их колбы откачивали до давления 10^-7 мм.рт.ст. [Е1], а в экспериментальных технических установках достигается давление ещё на несколько порядков ниже. Кроме того, могли быть использованы лазерные источники света, которые не только давали бы гораздо более мощный, чем у Лебедева, поток световой энергии, но и, при подходящем выборе рабочей длины волны, практически исключали бы действие света на остаточные газы. Однако, про сообщения о подобных опытах нам неизвестно. Трудно поверить в то, что никто не пытался ставить эти опыты. Проще поверить в то, что, после устранения радиометрических сил, пропадал и наблюдаемый силовой эффект. А чтобы публика-дура об этом не догадалась, придумали игрушку с замечательным названием: «радиометрическая вертушка». Светишь на её крыльчатку, а она и вертится! «Пусть вас не смущает название вертушки, - разъяснили публике, - она вертится из-за давления света!»

И вот, поскольку упорно не доказывался перенос импульса фотонами, когда они летели потоком, оставалась надежда лишь на доказательства переноса импульса отдельным фотоном. Считается, что первым таким доказательством стал эффект Комптона. Этот эффект заключается в рассеянии веществом рентгеновского излучения – с характерным увеличением его длины волны. Классическая теория рассеяния света не смогла объяснить этот феномен, и было принято объяснение Комптона [К1], основанное на подходе квантовой теории.

Согласно этому объяснению, рентгеновский фотон неупруго соударяется со слабо связанным атомарным электроном. При этом, как следует из законов сохранения энергии и импульса, часть своей энергии (и импульса) фотон передаёт электрону, выбивая его из атома и превращая в «электрон отдачи». В результате, как следует из законов сохранения энергии-импульса, длина волны фотона увеличивается. Такой подход согласуется с главными свойствами комптоновского сдвига длины волны: во-первых, с его независимостью от атомного номера вещества рассеивателя и, во-вторых, с его зависимостью лишь от угла, на который происходит рассеяние.

Однако, ради торжества подхода Комптона был проигнорирован ряд особенностей, с которыми этот подход не согласуется. Следует иметь в виду, что комптоновский сдвиг длины волны потому и заметен с помощью спектрометров, что в рассеянном на любой угол излучении присутствует также несмещённая компонента – с той же самой длиной волны, что и у падающего излучения. Если законы сохранения энергии-импульса дают, при рассеянии фотона на ненулевой угол, ненулевой комптоновский сдвиг длины волны, то неужели несмещённая компонента порождается с нарушением этих законов? Теоретики пытаются убедить нас в том, что несмещённая компонента порождается при таком соударении фотона с атомарным электроном, при котором электрон не выбивается из атома, т.е. фотон соударяется, фактически, не с электроном, а с атомом – а поскольку масса атома гораздо больше массы электрона, то импульс отдачи у атома оказывается ничтожен. Тогда теоретикам следовало бы объяснить, отчего фотон с энергией, которая на 3 порядка больше энергии связи атомарного электрона, в одних случаях выбивает электрон из атома, а в других случаях не выбивает – рассеиваясь при этом на один и тот же угол. Увы, разумного объяснения этому нет. Далее, не удаётся наблюдать комптоновское рассеяние на атомах сверхлёгких (в частности, водорода) и тяжёлых элементов – хотя свойства слабо связанных электронов у всех элементов ничем принципиально не различаются. Наконец, уничтожающим доводом против подхода Комптона является тот малоизвестный факт, что в рассеянном на любой угол излучении присутствует, помимо комптоновской и несмещённой компонент, ещё и компонента анти-комптоновская – длина волны которой уменьшена на величину комптоновского сдвига [С6]. В теорию Комптона совершенно не укладывалось наличие анти-комптоновской компоненты, поэтому он в известных нам публикациях даже не упоминал про неё.

Мы же, в работе [Г5], предлагаем более адекватное и честное объяснение феномена. Согласно нашей модели, рассеяние рентгеновских лучей здесь происходит не на атомарных электронах, а на нуклонных комплексах в ядрах – и при этом сдвиги длин волн зависят от «электронного» пространственного размера, от его комптоновской длины волны! Наша модель не только легко объясняет возможность всех трёх компонент: комптоновской, несмещённой и анти-комптоновской. Мы объясняем, почему эффект Комптона не наблюдается при рассеянии рентгеновских лучей на атомах сверхлёгких элементов, например, на водороде – у водорода нет требуемых для этого нуклонных комплексов. Мы объясняем, почему эффект Комптона не наблюдается при рассеянии рентгеновских лучей на атомах тяжёлых элементов – хотя эти атомы, конечно, тоже имеют «слабо связанные» электроны. Разгадка здесь, на наш взгляд, в том, что рентгеновские кванты эффективно взаимодействуют с электронами из внутренних электронных оболочек тяжёлых атомов – отчего эти кванты попросту «не добираются» до ядер. Наконец, мы объясняем, почему эффект Комптона не наблюдается для видимого света – хотя, согласно логике квантовой теории рассеяния, комптоновские сдвиги здесь вполне могли бы иметь место, а их наблюдение не представляло бы особых технических сложностей. Разгадка в том, что видимый-то свет рассеивается именно атомарными электронами, а не нуклонными комплексами в ядрах.

И ещё: в отличие от модели Комптона, которая требует наличия выбиваемых из атомов «электронов отдачи», по нашей модели, никаких «электронов отдачи» не существует. А ведь был проведён целый ряд экспериментов [Ш3,Х1,К2], призванных подкрепить шаткие представления Комптона и проиллюстрировать разлёт продуктов комптоновского рассеяния – при котором рассеянный квант и «электрон отдачи» вылетают из атома одновременно и разлетаются под «правильными» углами. В работе [Г5] дан критический обзор подобных экспериментов, и показана их полная бездоказательность. Их общим недостатком было отсутствие доказательств того, что исследовалось именно комптоновское рассеяние – измерением комптоновских сдвигов здесь никто себя не утруждал. Впрочем, в некоторых «подтверждающих» опытах использовали в качестве первичного излучения гамма-кванты [Х1,К2], у которых измерять комптоновские сдвиги было просто нечем [Г5]. Так, Крэйн, Гартнер и Турин [К2] поместили мишень-рассеиватель в центре камеры Вильсона – для проверки того, что направления вылета электрона отдачи и рассеянного фотона находятся в согласии с законами сохранения энергии-импульса. В качестве первичного излучения использовались жёсткие гамма-лучи – что делало весьма сомнительной саму возможность комптоновского рассеяния. Электроны, которые, судя по их трекам, вылетали из мишени вперёд, считались электронами отдачи – хотя они могли быть электронами внутренней конверсии или фотоэлектронами, выбиваемыми вторичными гамма-квантами. Поскольку гамма-квант не оставляет трека в камере Вильсона, то, для подтверждения «правильного» направления полёта рассеянного гамма-кванта, требовалось получить «правильные» фотографии. А именно: на них, помимо трека «электрона отдачи», требовалось зафиксировать, в «правильном» сегменте камеры, трек ещё одного электрона – якобы, выбитого рассеянным гамма-квантом. Мы говорим «якобы», поскольку никаких гарантий того, что второй электрон выбивался гамма-квантом, вылетавшим из мишени в центре камеры, быть не могло. При таком положении дел, «правильная» пара треков могла получаться лишь в результате маловероятного стечения случайных обстоятельств, на ничтожном проценте фотографий – как это и было в действительности. Обработав только эти «удачные» фотографии, авторы сделали неизбежный, при подобном высоконаучном подходе, вывод о том, что «наблюдаемый угол полёта рассеянного фотона совпадает с вычисленным» [Ш1]. Вот такой лепет нам подсовывают в качестве подпорок заявлений Комптона – насчёт того, что фотон переносит импульс! Добавим, что скептические слова в адрес традиционной интерпретации комптоновских сдвигов, а также критические замечания по поводу экспериментов с «электронами отдачи» высказывались и ранее – например, в исследовании [А1].

Ещё одним эффектом, который, как полагают, доказывает перенос импульса гамма-квантом, является эффект Мёссбауэра. До открытия Мёссбауэра, наблюдение резонансного ядерного поглощения было затруднено – как считалось, из-за эффекта отдачи: гамма-квант, якобы, передаёт часть своего импульса как излучающему его ядру, так и поглощающему, отчего их совпадающие невозмущённые линии «разъезжаются» из-за эффекта Допплера. Это объяснение – недоразумение какое-то. Допплеровский сдвиг линии излучателя имеет место, когда соответствующая скорость у излучателя уже имеется. В рассматриваемом же случае эта скорость приобретается в результате отдачи, т.е. после того, как излучение гамма-кванта уже произошло. Аналогично, у ядра-поглотителя допплеровский сдвиг линии, из-за эффекта отдачи, мог бы появиться лишь после того, как уже произошло поглощение. Ну, никак не мог эффект отдачи портить резонансное ядерное поглощение! Но нам предъявляют факты: при сближении излучателя и поглотителя, вероятность этого поглощения увеличивалась. Казалось бы, здесь происходила допплеровская компенсация эффекта отдачи. И, когда Мёссбауэр обнаружил резонансное поглощение при отсутствии допплеровской компенсации, а при условиях, когда ядра-излучатели и ядра-поглотители входили в состав кристаллических структур, находившихся при достаточно низкой температуре – был сделан вывод о том, что здесь отдача от гамма-кванта воспринимается не одиночным ядром, а всем кристаллом в целом, становясь при этом, практически, нулевой.

Казалось бы, всё логично? Отнюдь. Наш анализ показал, что в тех самых опытах по «допплеровской компенсации» эффекта отдачи имела место селекция опытных данных: та их часть, которая не согласовывалась с концепцией отдачи от гамма-кванта – несомненно, замалчивалась [Г6]. В лучшем согласии с опытными данными оказывается наша модель [Г6] – согласно которой, резонансному ядерному поглощению в обычных условиях препятствует не «эффект отдачи», а допплеровские смещения, обусловленные тепловыми колебаниями ядер в твёрдых телах. При достаточно низких температурах, когда размах тепловых колебаний ядер становится меньше длины волны гамма-излучения, допплеровские смещения становятся нулевыми из-за эффекта Лэмба-Дика – и имеет место мёссбауэровский режим. Из нашего подхода следует, что, у конкретного кристалла, переход в мёссбауэровский режим для различных длин волн гамма-излучения происходит при различных температурах – а не при одной и той же, дебаевской, как это следует из традиционного подхода. Именно наш подход лучше согласуется с опытом: чего стоит один лишь факт мёссбауэровского поглощения для перехода 14.4 кэВ у железа при температурах вплоть до 1046^оК [Н1], хотя дебаевская температура у железа равна 467^оК [Ф1]. Кроме того, из нашего подхода следует, что мёссбауэровские ширины определяются не естественными ширинами ядерных линий, а параметрами кристаллической решётки, которая в мёссбауэровском режиме является высокодобротным интерференционным фильтром. Следствием этого вывода является предсказание об анизотропии эффекта Мёссбауэра для монокристаллических образцов – что действительно имеет место [А2,Г7,К3,А3]. Любое объяснение этой анизотропии с позиций традиционного подхода является противоречивым, поскольку здесь для кристаллической решётки подразумевается абсолютная жёсткость, при которой отдача от гамма-кванта воспринимается «всем кристаллом» одинаково во всех направлениях. По совокупности, традиционный подход, в котором гамма-кванты переносят импульс, вновь оказывается неадекватен экспериментальным реалиям.

С началом эры освоения космоса появились, как полагают, свидетельства о том, что давление солнечного света влияет на движение космических аппаратов. Так, в 1960 г. на околоземную орбиту был выведен американский спутник «Эхо-1». В развёрнутом состоянии он представлял собой сферический баллон из майларовой плёнки, металлизированной снаружи. При диаметре баллона 30 м и массе всего 68 кг, спутник имел «большую «парусность» по отношению к давлению солнечного света» [Л4]. За пять месяцев орбита спутника из почти круговой (высота перигея 1520 км, высота апогея 1687 км [К4]) превратилась в эллиптическую (высота перигея 900 км, высота апогея 2200 км [Л4]), за следующие полгода вновь возвратилась к почти круговой, после чего опять стала вытягиваться, и так далее. Торможение о разреженную атмосферу, особенно на перигейных участках, приводило к постепенному опусканию орбиты, и в итоге «Эхо-1» просуществовал на орбите менее восьми лет. Всё выглядело очень похоже на то, что эволюции орбиты «Эхо-1» вызывались действием давления солнечного света [Ш2,М1].

Но мы усмотрели другую причину этих эволюций орбиты – чисто электромагнитную. Ультрафиолетовое излучение Солнца должно было вырывать фотоэлектроны из металлизированной поверхности спутника, заряжая его положительно. Компенсирующий приток электронов из окружающего пространства происходил бы не изотропно: из-за магнитного действия фотоэлектронов, летевших, в основном, в сторону Солнца, притекавшие электроны формировали бы область избыточной концентрации отрицательного заряда с противосолнечной стороны от баллона. Этот избыточный отрицательный заряд притягивал бы положительно заряженный баллон – вот и источник силы, тянувшей его в направлении «от Солнца», когда спутник не находился в тени. Оценки [Г8] показывают: этот механизм вполне реалистичен, поэтому эволюции орбиты спутника «Эхо-1» нельзя считать доказательством того, что их причиной было давление солнечного света.

Далее, после создания узкополосных перестраиваемых лазеров, бурно развивается спектроскопия атомов и ионов, охлаждённых и удерживаемых лазерным излучением (см., например, обзор [Д1]). Лазерное охлаждение атомов и ионов, а также их удержание в оптических ловушках, считаются несомненными свидетельствами передачи этим атомам и ионам импульсов фотонов, которых они резонансно поглощают. Но, на наш взгляд [Г4], здесь происходят совсем иные процессы.

Так, в радиочастотной ловушке ионы совершают колебания в области устойчивого движения. Для лазерного охлаждения облачка ионов, его подсвечивают лазерным лучом, частота которого ниже частоты «охлаждающего» оптического перехода у ионов – с таким расчётом, что ионы, движущиеся навстречу лазерным фотонам, воспринимают их допплеровски увеличенную частоту как резонансную, и эффективно их поглощают. Переизлучение же поглощённых фотонов, как полагают, происходит спонтанно, в произвольном направлении. По этой логике, при поглощении фотонов у иона накапливается тормозящий импульс, а при их переизлучении усреднённый импульс отдачи стремится к нулю – так что колебательные движения иона гасятся, вплоть до эквивалентных температур в сотни и даже десятки микроКельвинов.

Мы же полагаем, что гашение колебаний здесь происходит иначе. Бесспорно, что при поглощении ионом порции световой энергии hf, масса иона увеличивается на величину hf/c², а при излучении такой же порции энергии, масса иона уменьшается до прежнего значения. Эти повторяющиеся увеличения-уменьшения массы колеблющегося иона могут привести – без какой бы то ни было передачи импульса – либо к параметрическому гашению колебаний иона, либо, наоборот, к их параметрической раскачке. Поскольку нет гарантий, что циклы увеличения-уменьшения массы иона синхронизированы с циклами его колебаний, то ясно, что параметрическое гашение колебаний будет происходить с меньшей вероятностью, чем их параметрическая раскачка. И, действительно, лишь ничтожный процент ионов из облачка испытывает «лазерное охлаждение» - а остальные, наоборот, покидают зону устойчивого движения. Заметим, что параметрическое гашение колебаний у части ионов должно происходить с неменьшим успехом в случае, когда частота лазера выше частоты оптического перехода, т.е. когда резонансно поглощают ионы, движущиеся попутно с фотонами – хотя, согласно традиционной логике, в такой ситуации должен иметь место «лазерный разогрев» ионов.

Ещё один важный экспериментальный результат – это удержание атомов лазерными лучами. Так, в стандарте частоты, называемом «цезиевый фонтан» (см., например, [Д2]), облачко атомов цезия удерживается в «холодном», т.е., практически, в неподвижном состоянии благодаря подсветке, с шести сторон, лазерными лучами, частота которых на ~5 МГц ниже невозмущённой частоты оптического перехода (?=852 нм) в цезии. Считается, что при движении атома, уводящем его из области перекрестья лучей, он резонансно поглощает фотоны встречного луча и, таким образом, тормозится из-за эффекта отдачи.

Мы же полагаем, что и в данном случае дело заключается не в эффекте отдачи. Находящийся в движении атом воспринимает, из-за эффекта Допплера, частоту встречного луча увеличенной, а частоту попутного луча – уменьшенной. При этом, поразительным образом, искусственно имитируется пребывание атома в условиях градиента частот (2.7), который порождает силовое воздействие, направленное в сторону понижения частот. В результате атом приобретает тормозящее ускорение – как это происходит согласно нашей модели действия тяготения на вещество (2.7).

Добавим, что на том же самом принципе – имитации градиента частот – производится подброс облачка атомов в «цезиевом фонтане». Для этого частоты лазеров, подсвечивающих облачко сверху и снизу, на время порядка одной миллисекунды сдвигают на несколько МГц – частоту подсветки сверху уменьшают, а частоту подсветки снизу увеличивают. В результате этой процедуры облачко атомов, испытавших кратковременную имитацию вертикального градиента частот, начинает свой свободный полёт вверх. Разумеется, традиционный подход объясняет такой подброс облачка атомов иначе – как результат накопления импульсов поглощённых фотонов из подсветки снизу. Для того, чтобы таким способом атому цезия была сообщена скорость в несколько метров в секунду, он должен накопить импульс от ~1000 оптических фотонов – что, за время «подбрасывающего режима», вполне возможно. Но обратим внимание на одно важное обстоятельство. Из опыта достоверно известно, что начальная скорость свободного полёта облачка ионов вверх – по окончании «подбрасывающего режима» - прямо пропорциональна применённой разности частот подсветок снизу и сверху. Между тем, увеличение этой разности частот отнюдь не должно приводить к прямо пропорциональному увеличению числа поглощённых фотонов за время «подбрасывающего режима». Импульсы же этих фотонов, практически, не изменяются при изменении их частоты на несколько МГц. Отчего же усиливается подброс при увеличении разности частот подсветок снизу и сверху? Наше объяснение, через имитацию градиента частот, выглядит предпочтительнее! Похоже, мы имеем здесь дело с парадоксальной ситуацией: экспериментаторы научились искусственно создавать условия, при которых возникает безопорное движение атомов – но, не веря глазам своим, пытаются втиснуть эти результаты в рамки традиционных понятий.

Кстати, нам даже приводили аргументы насчёт давления света, полученные, так сказать, на личном опыте. «Я своей шкурой чувствовал давление света, - рассказывал один. – Был в рубашке, и мне в спину попадали импульсы инфракрасного лазерного дальномера. Каждый импульс отлично чувствовался – не через тепло, а через лёгкое тактильное ощущение!» Неубедительно, профессор! Это тактильное ощущение вызывалось, скорее всего, небольшим местным повышением давления воздуха между спиной и рубашкой – из-за небольшого повышения его температуры. Порог тепловой чувствительности кожи не превышался, а порог тактильной чувствительности – превышался. Вот и всё объяснение. «А ещё, - кричали, - при лазерном воздействии – если мелкий образец не закрепить, то его просто снесёт давлением лазерного излучения!» Друзья, мне самому не чужда тема лазерной обработки материалов. И мне хорошо известно, что из кратера, образуемого лазерным излучением на образце, вылетают, как минимум, продукты испарения материала, а, при неудачно подобранном режиме – ещё и брызги жидкой фазы. Из-за выброса этих масс и возникает «отдача», действующая на образец. Ничего общего с «давлением света» это не имеет.

На основе вышеизложенного, мы не усматриваем экспериментальных свидетельств о том, что фотоны переносят импульс. Что же касается теоретических измышлений – о том, что в звёздах-гигантах свет, идущий из недр, сдерживает их гравитационное сжатие, или о том, что в эпицентре ядерного взрыва давление света так велико, что им и порождается ударная волна – то к этим измышлениям мы не будем относиться серьёзно. Пусть теоретики веруют в давление света. Их так воспитали: когда они были маленькими, им рассказывали сказки про фотонные ракеты. Кто ж виноват в том, что с возрастом они так и не поняли, что это были сказки?

В 1966 г. Басов и сотрудники [Б2] впервые сообщили об эффекте, который до сих пор не имеет разумного объяснения в рамках традиционных физических концепций. Эти авторы исследовали временные задержки на движение лазерного импульса в системе генератор-усилитель. Пара рубиновых стержней-усилителей находилась на расстоянии около 2.5 м от рубинового лазера-генератора. Между генератором и усилителем была установлена делительная пластинка, которая отбирала часть энергии лазерного импульса и направляла её по другому пути, не проходящему через усилитель. Таким образом, лазерный импульс расщеплялся на два, каждый из которых попадал на свой фотодетектор, сигналы с которых подавались на скоростной двухканальный осциллограф. Методика измерений была совсем простой. При выключенном усилителе, т.е. при отключенных лампах его накачки, согласовывали задержки в электрических трактах двух каналов так, чтобы на экране осциллографа оба всплеска фототока происходили синхронно. А потом – повторяли опыт при единственном изменённом условии: при включённом усилителе. И оказывалось, что всплеск фототока от импульса, проходившего через усилитель, теперь опережал во времени другой всплеск, который служил опорным. Изумляла величина этого опережения: она была запредельно велика. Казалось бы: изменения, которые могли уменьшить задержку, происходили лишь на протяжении усилителя. Если допустить немыслимую ситуацию, при которой лазерный импульс проходил бы по включённому усилителю мгновенно, то даже тогда выигрыш во времени составил бы всего около 1.6 наносекунды. А осциллограф чётко показывал: не 1.6, а целых 9 наносекунд! При длительности самого импульса в 3 наносекунды, эффект обнаруживался вполне убедительно – как впоследствии и у других групп исследователей, использовавших среды с различными типами нелинейностей [Ч1,С4,А4,В1].

Мы расцениваем опыт Басова как один из величайших экспериментов ХХ века. Поразительно, как с помощью минимума технических средств можно было получить ошеломляющий результат, который прямо и просто, без всяких кривотолков и «интертрепаций», показал: представления ортодоксальной науки о свете, как о летящих фотонах – причём, летящих со скоростью света – это полная чушь. Проверено: ортодоксы, узнающие про результат Басова, впадают в прострацию и оказываются неспособны сказать по существу ничего членораздельного. Впрочем, были попытки заболтать этот результат и показать, что он «на самом деле ничему не противоречит». Развернулась некоторая деятельность теоретиков, к которой вполне подходит определение «театр абсурда». Ибо теоретики взялись сооружать модели движения лазерного импульса в усилителе со скоростью, превышающей скорость света в вакууме – даже не заикаясь о том, что сама постановка такой задачи повергает в прах специальную теорию относительности (СТО). Вот, например, до чего они додумались (см. обзор [О1]). При движении лазерного импульса в усиливающей среде, коэффициент усиления для переднего фронта импульса больше, чем для заднего, поскольку задний фронт движется по среде, уже частично «высветившейся». Эта неодинаковость коэффициентов усиления приводит к тому, что передний фронт приподнимается над пьедесталом импульса, а задний фронт – приопускается, что в итоге эквивалентно продвижению импульса вперёд по пьедесталу. Складывая скорость движения пьедестала и скорость «усилительного сноса», получали сверхсветовую скорость движения импульса. Самое смешное в этом объяснении было то, что в нём использовалось классическое сложение скоростей, а не релятивистское – которое следовало бы использовать ортодоксам для случая, когда одним из слагаемых являлась скорость света. Куда ж деваться – результатом релятивистского сложения скоростей никак не может быть скорость, большая скорости света в вакууме! Ну, а самое печальное в этом объяснении было то, что оно ровным счётом ничего не объясняло. Во-первых, сокращение времени движения импульса при «включённой» нелинейности в ячейке имело место не только для усиливающих, но, как выяснилось позже, и для поглощающих сред [В1] – лишь бы совпадали спектральные линии у генератора и у нелинейной ячейки. Как интересно: для сверхсветовой скорости лазерного импульса требуется попадание на спектральную линию – как и для сверхсветовой фазовой скорости на линии поглощения в веществе, о чём давно хорошо известно! А, во-вторых, русским же языком было сказано: импульс не просто двигался в ячейке со сверхсветовой скоростью – выигрыш во времени был больше того, каков он был бы при мгновенном прохождении ячейки! Так, в случае, когда роль нелинейной ячейки играла тонкая поглощающая плёнка [В1], обнаруженный выигрыш во времени превышал выигрыш при мгновенном прохождении этой плёнки в 310 раз! Либо этот оглушительный результат негативно сказался на рассудке авторов – ибо они в серьёзном научном журнале заявили о том, что лазерный импульс в нелинейной ячейке движется вперёд по пространству, но вспять во времени: «импульс появляется на выходе ячейки до того, как он входит в неё» [В1] (перевод наш). Либо, будучи в своём обычном рассудке, авторы специально выдали этот абсурд – чтобы зациклить на нём внимание публики, которая иначе зациклилась бы на очевидном крахе СТО. Представляете, на какие жертвы пришлось идти этим авторам, следуя велениям научного долга? Мол, пусть лучше нас считают идиотами или негодяями – лишь бы мы репутацию СТО не подмочили!

И, вот, спрашивается: а стоит ли идти на такие жертвы? Если до такого дошло – не пора ли призадуматься насчёт корректности основных исходных представлений? Не смешно ли ставить задачу так: «Каким образом лазерный импульс проходит по нелинейной ячейке быстрее, чем мгновенно? или, другими словами, каким образом групповая скорость света может быть больше, чем бесконечная?» Может, здесь дело не только в нелинейной ячейке? Ведь во всех подобных экспериментах «выпадающая» задержка – это как раз время, равное расстоянию от генератора до нелинейной ячейки, делённому на скорость света! Во сколько раз это расстояние превышает длину пути света в нелинейной ячейке, во столько раз наблюдаемый выигрыш во времени оказывается больше выигрыша при «мгновенном» прохождении ячейки! О чём это говорит? О том, что когда нелинейность «выключена», лазерный импульс идёт от генератора к нелинейной ячейке со скоростью света, а когда нелинейность «включена», лазерный импульс перебрасывается из генератора в нелинейную ячейку, практически, мгновенно. Тогда мы немедленно получаем идеальное согласие с опытными данными – без насилия над здравым смыслом и без противоречий не только с принципом причинности, но и с элементарными представлениями о движении. Всё в этих опытах становится на свои места; остаётся лишь объяснить – каким образом лазерный импульс перебрасывается мгновенно на расстояние, по крайней мере, в несколько метров.

В рамках традиционных представлений о свете, этот феномен, конечно, не объясняется. По логике же «цифрового» мира, этот феномен совершенно естественен – являясь частным проявлением общего случая распространения света, как цепочки мгновенных квантовых перебросов энергии возбуждения с атома на атом. При этом конечность скорости света, а не её бесконечность, обусловлена конечным быстродействием алгоритма, «прокладывающего путь», по которому производится такая цепочка квантовых перебросов. Этот алгоритм мы называем «навигатором квантовых перебросов энергии».

Атом может приобрести энергию возбуждения в результате её квантового переброса с другого атома. Аналогично, атом может избавиться от энергии возбуждения с помощью её квантового переброса на другой атом. Квантовый переброс энергии возбуждения с атома на атом – это элементарный акт продвижения кванта световой энергии. При этом световая энергия вне атомов не существует: будучи до квантового переброса энергией возбуждения атома-отправителя, после квантового переброса она становится энергией возбуждения атома-получателя. Т.е., никакого движения световой энергии по пространству, разделяющему атомы, не происходит – ни в виде волн, ни в виде фотонов. Квант энергии возбуждения перебрасывается непосредственно с одного атома на другой – что осуществляется чисто программными манипуляциями.

Такое скачкообразное перемещение энергии возбуждения легко промоделировать на компьютере. Пусть два пульсирующих кружка на экране монитора, разделённые некоторым расстоянием, будут символизировать нашу пару атомов. Пусть частота пульсаций одного из них будет равна f₁, а второго – f₂. Программа, иллюстрирующая идею квантового переброса, должна одномоментно изменить значения частот пульсаций: частоту f₁ уменьшить на величину ?f, а частоту f₂ увеличить на ту же величину ?f. В более адекватной компьютерной модели, изменения частот пульсаций должны осуществляться не за один рабочий такт, а за время, обратное величине ?f – как это, по-видимому, происходит при настоящем квантовом перебросе, а именно, в согласии с известным соотношением E?~h (где E - перебрасываемая энергия возбуждения, ? - длительность переброса, h - постоянная Планка). При этом длительность ? квантового переброса не зависит от расстояния между соответствующей парой атомов. Чем больше перебрасываемая энергия возбуждения и чем больше разреженность вещественной среды, тем с большей степенью приближения проявляется практическая «мгновенность» квантовых перебросов в этой среде.

В самом деле, если формально рассчитывать скорость квантового переброса, деля на его длительность расстояние между соответствующей парой атомов, то результатом могут быть скорости, на много порядков превышающие скорость света в вакууме. Но мы не усматриваем здесь противоречия с принципом причинности, ведь здесь мы имеем дело с особым способом перемещения световой энергии – с её скачкообразным переносом на расстояние. Физически бессмысленно говорить о скорости такого перемещения, поскольку, при его одной и той же ничтожной длительности, его скорость неоднозначна, будучи функцией расстояния между парой соответствующих атомов. Кстати, отсюда немедленно следует, что если при квантовом перебросе происходила бы передача импульса, то величина этого импульса была бы так же неоднозначна, как и скорость переброса. Но поскольку, при квантовом перебросе, световая энергия передаётся с атома на атом без физического посредника, который переносил бы импульс – то, на наш взгляд, совершенно логично выглядит вывод о том, что при квантовом перебросе световой энергии не передаётся импульс. Выше мы уже разобрали экспериментальную сторону этого вопроса: никаких опытных данных, свидетельствующих о переносе светом импульса, не существует (3.2).

Разумеется, одной лишь моделью движения кванта световой энергии, как цепочки её квантовых перебросов с атома на атом, нельзя объяснить происхождение даже основных законов распространения света. Квантовый переброс происходит уже после того, как для атома, имеющего энергию возбуждения, будет выбран партнёр – адресат передачи. Квантовый переброс лишь венчает работу алгоритма, осуществляющего поиск и выбор этого адресата. А законы распространения света, во всём их парадоксальном великолепии, оказываются следствиями работы этого алгоритма – навигатора квантовых перебросов энергии (далее – Навигатора) [Г9].

Как только атом приобретает энергию возбуждения, немедленно начинается работа Навигатора, т.е. процесс поиска атома-адресата, которому энергия возбуждения может быть переброшена. Работа Навигатора, который, фактически, «прокладывает путь» для перебрасываемой энергии возбуждения, имеет чисто алгоритмический характер. В ходе этой работы вычисляются, для точек вокруг возбуждённого атома, текущие вероятности, с которыми в эти точки мог бы быть произведён квантовый переброс. В качестве атома-адресата выбирается, при прочих равных условиях, атом в такой точке, для которой вероятность переброса оказывается максимальна.

Картина пространственного распределения расчётных вероятностей является не статической, а динамической: от возбуждённого атома расходится, со скоростью света в вакууме, сферическая волна с чередующимися максимумами и минимумами вероятностей. Следует чётко понимать, что эта волна, при своём движении, не переносит физической энергии и не оказывает никакого воздействия ни на геометрию пространства-времени, ни на вещество. Эта волна, если можно так выразиться, всего лишь сканирует пространство в поисках атома-адресата. У первого же атома, которого накрывает передний горб расчётных вероятностей, появляется шанс стать этим адресатом.

На основе того, что мы уже успели сказать о работе Навигатора, мы можем объяснить, почему движение световой энергии, которое мы представляем как последовательность «практически мгновенных» квантовых перебросов, происходит всё-таки с конечной скоростью. Действительно, путь световой энергии прокладывает Навигатор, поэтому она никак не может обогнать переднего фронта волны расчётных вероятностей. Причём, до тех пор, пока Навигатор не выберет атома-получателя, перебрасываемая энергия находится на атоме-отправителе. Впрочем, возможны и такие ситуации: Навигатор начинает поиск, но не успевает его завершить из-за какого-либо события с атомом-отправителем, например, из-за потери им энергии возбуждения в результате столкновения с другим атомом. Тогда поиск прерывается – без каких-либо последствий для физического мира.

Объясняется и ещё одно известное свойство света: пересекающиеся пучки света не мешают друг другу (в линейном режиме). Мы до сих пор обсуждали отдельно взятый квантовый переброс, но физический мир бурлит ими, и для каждого возбуждённого атома работает свой канал Навигатора. Соответствующие различные волны расчётных вероятностей совместно сканируют одни и те же области пространства. Но разве могут эти волны мешать друг другу? Они являются, если можно так выразиться, информационной реальностью – по сути дела, параллельно проводимыми расчётами – и, конечно же, мешать друг другу не должны.

Уточним некоторые свойства волны расчётных вероятностей – в первую очередь, вид её пространственного профиля. Как уже упоминалось выше, этот профиль имеет периодичность: соседние слои наибольших вероятностей отстоят друг от друга на расстояние, которое играет роль «длины волны». Откуда Навигатор «знает», какую длину волны создавать у волны расчётных вероятностей? Длина волны ? связана с величиной энергии возбуждения E через соотношение ?=hc/E, т.е. длина волны «известна» сразу же после возбуждения атома-отправителя. Что же касается формы профиля волны расчётных вероятностей, то, в духе «цифровых» первооснов физического мира, эта форма представляет собой не синусоиду, а, скорее, гребёнку из узких пиков ненулевой вероятности переброса, разделённых промежутками нулевой вероятности переброса. Иллюстрацией результирующей волны в целом может быть набор вложенных друг в друга расширяющихся мыльных пузырей, оболочки которых соответствуют слоям ненулевой вероятности переброса.

Из вышеизложенного следует, что, для каждого момента времени, квантовый переброс энергии возбуждения может быть выполнен лишь на дискретные расстояния – через промежутки, равные длине волны – и что начальное распределение вероятностей переброса имеет сферическую симметрию. Однако, эта сферическая симметрия нарушается сразу после того, как передний фронт волны расчётных вероятностей дойдёт до ближайшего атома. Если этот атом не выбирается в качестве адресата, и на него сразу же не производится квантовый переброс, то этот атом идентифицируется Навигатором как неоднородность, которая, по аналогии с принципом Гюйгенса-Френеля, становится «источником» вторичной сферической волны расчётных вероятностей. Эта вторичная волна имеет ту же длину волны, что и первичная волна, и синхронизирована с ней по фазе следующим образом: очередная сфера ненулевых вероятностей вторичной волны начинает своё расширение в момент прохождения очередной сферы ненулевых вероятностей первичной волны. Тогда, как можно видеть, эти сферы у вторичной и первичной волн расширяются, сохраняя касания друг друга в точках, которые движутся вдоль геометрического луча, проведённого от центра первичной волны через центр вторичной волны. Примем во внимание, что суммарная расчётная вероятность переброса в точки, которые «накрывают» пики ненулевых вероятностей сразу двух волн – и первичной, и вторичной – существенно возрастает (в относительном исчислении; полная расчётная вероятность переброса для всей области, которую успел просканировать Навигатор, очевидно, всегда равна единице). Значит, существенно возрастает вероятность переброса в выделенном направлении – по тому самому геометрическому лучу.

По этой логике работы Навигатора, выделенных направлений максимально вероятного переброса может образоваться несколько – по числу атомов из ближайшего окружения атома-отправителя. Это – примечательный вывод! Он позволяет сразу же объяснить, почему упорядоченные атомные структуры – например, монокристаллы – рассеивают попадающий в них свет не изотропно, а, преимущественно, в выделенных направлениях: вдоль лучей, на которые «нанизаны» их атомы.

Но вернёмся к нашему атому-отправителю. Вот, наконец, в одном из направлений максимально вероятного переброса, Навигатор делает выбор атома-получателя, и квантовый переброс энергии возбуждения происходит. На этом, вообще говоря, не завершается работа канала Навигатора, прокладывающего путь этой порции энергии. Работа завершится тогда, когда эта порция энергии уже не сможет быть передана дальше – например, после превращения её в иную форму энергии. А до тех пор, получивший порцию энергии атом сразу же становится «источником» новой волны расчётных вероятностей, которая «генерируется» по описанному выше алгоритму вторичной волны. Отсюда сразу же следует естественное объяснение феномена прямолинейного распространения света.

Впрочем, известен ряд факторов, которые приводят к тем или иным отклонениям от этой прямолинейности. Прежде всего, при совместном распространении первичной и вторичной волн расчётных вероятностей, максимальные вероятности переброса приходятся не просто на точки касания сфер этих волн, как это описано выше, а на несколько большие области касания, имеющие ненулевые размеры: толщины и поперечные радиусы. Эти поперечные радиусы областей касания увеличиваются по мере продвижения первичной и вторичной волн – из-за того, что увеличиваются радиусы сфер этих волн. Соответственно, увеличиваются поперечные радиусы областей максимальных вероятностей переброса, чем и объясняется – по крайней мере, качественно – дифракционная расходимость света.

Кроме того, ненулевые поперечные радиусы областей максимальных вероятностей переброса приводят, на наш взгляд, ещё к нескольким известным феноменам. Один из них – это рефракция, т.е. искривление путей распространения света в среде с градиентом концентрации атомов. Например, в атмосфере с нормальным вертикальным градиентом плотности, «лепёшки» максимальных вероятностей будут систематически накрывать большее число атомов своими нижними половинками, чем верхними. Поэтому «источников» вторичных волн будет больше в нижней части створа максимальных вероятностей, и в результате этот створ будет «заворачивать» вниз.

Аналогично происходит преломление света при переходе через плоскую границу раздела двух прозрачных сред с различными концентрациями атомов. Отличие преломления от рефракции заключается лишь в следующем: если асимметрия «генерации» вторичных волн, о которой идёт речь, имеет место на протяжении всего пути распространения света, то происходит рефракция, а если эта асимметрия имеет место только при переходе через границу сред, то происходит преломление – фактически, импульсная рефракция. Заметим: чем короче длина волны расчётных вероятностей, тем, при прочих равных условиях, больше суммарный эффект от асимметрии «генерации» вторичных волн. Следовательно, коротковолновое излучение должно преломляться сильнее, чем длинноволновое – что и происходит в действительности.

На наш взгляд, волна расчётных вероятностей в вещественной среде, по сравнению со случаем вакуума, уменьшает свою скорость из-за сбоев в продвижении её переднего фронта – например, из-за безызлучательной потери энергии возбуждения тем или иным атомом-отправителем – что эквивалентно «задержкам в пути». Причём, чем короче длина волны, тем, на одном и том же отрезке среды, большее число атомов накрывается «лепёшками» максимальных вероятностей – значит, тем больше среднее число сбоев и задержек на единицу длины, и тем больше результирующее замедление волны. Таким образом, мы качественно объяснили нормальную дисперсию света в веществе. Более того, описанный механизм замедления волны в среде позволяет построить оптику движущихся сред: на его основе получается выражение для фазовой скорости света в движущейся среде, которое в нерелятивистском приближении даёт знаменитый френелевский «коэффициент увлечения» света движущимся веществом [Г9].

По поводу поляризационных эффектов заметим: из приведённого выше описания волн расчётных вероятностей ясно, что этим волнам не присуще такое свойство, как поперечность, поэтому они никоим образом не могут быть поляризованы – в традиционном понимании этого термина. Поляризационные эффекты обусловлены, по-видимому, дополнительными изменениями форм областей максимальной вероятности переброса – из-за «генерации» вторичных волн атомами, которые упорядоченно расположены либо в молекулах, либо в кристаллических решётках.

Наконец, поясним причину «запредельных» опережений у Басова и его последователей (3.3). Навигатор прокладывает путь квантам энергии возбуждения особенно эффективно, когда длина волны попадает на спектральную линию в веществе. А, в рассматриваемом случае, у генератора и нелинейной ячейки спектральная линия одна и та же. Лазерный импульс генерируется не мгновенно – и, когда он сгенерирован, готовый путь ему уже проложен до выходного торца нелинейной ячейки. Почти мгновенный переброс квантов энергии возбуждения из генератора в нелинейную ячейку происходит точно так же, как их почти мгновенные перебросы с атома на атом в генераторе.

Что касается объяснения волновых свойств света, то этот вопрос мы рассмотрим в отдельном параграфе (3.5).

Основное волновое явление при распространении света – интерференция. При прохождении светом, например, сквозь систему из множества параллельных щелей, получается интерференционная картинка – чередование светлых и тёмных полос. Волновая теория легко объясняет эту картинку. Волновой фронт, проходя сквозь эти щели, дробится на множество участочков, которые становятся источниками вторичных волн. Складываясь, эти вторичные волны либо усиливают друг друга, либо, наоборот, гасят – в соответствии с разностью фаз, которая зависит от направления распространения света за щелями. Там, где волны складываются синфазно, получаются светлые полосы, а там, где они складываются противофазно – тёмные. Но как объяснить эту картинку, если представлять свет летящими фотонами? Если фотон – полноценная частица, то он должен пролетать сквозь какую-то одну щель, а не сквозь несколько щелей сразу. Откуда же тогда взяться интерференционной картинке? Кстати: чем больше щелей, тем эта картинка резче. Что же, фотон пролетает сквозь одну щель, но чувствует все остальные?

Поразительно, но даже этот простейший случай ортодоксальная наука до сих пор не может объяснить – на основе концепции летящих фотонов. Сначала говорили, что каждый фотон проходит сквозь какую-то одну щель, но полосы получаются, когда фотонов пролетает много. После щелей они, якобы, накладываются друг на друга – вот, мол, и получаются полосы, как и в случае волн… Нет, так не пойдёт! Если фазы у фотонов при прохождении щелей распределены случайным образом – а это обычное дело при нелазерных источниках света – то никакой системы светлых и тёмных полос не получится: чтобы она получилась, нужна одна и та же фаза при прохождении щелей. Но ведь эта система полос успешно получается! Значит, можно заподозрить, что дело здесь вовсе не в наложении фотонов друг на друга. И точно, известны опытные факты, свидетельствующие о том, что интерференционная картинка получается отнюдь не в результате взаимодействия фотонов друг с другом. Были специально поставлены опыты при сверхслабых световых потоках: фотоны летели, практически, поодиночке – и, лишь после длительной экспозиции, на результирующей фотопластинке можно было что-то разглядеть (описание этих опытов см., например, в [Т1]). Выяснилось: картинки, полученные при обычных световых потоках и малых временах экспозиции, идентичны картинкам, полученным при сверхслабых световых потоках и достаточно длительных экспозициях. Ну, и чего? Помогли эти результаты ортодоксам понять, что в концепции летящих фотонов – что-то очень не так? Да ничуть. Наоборот, вот куда понесло иных теоретиков: «Раз уж полосы получаются даже тогда, когда фотоны летят поодиночке, то имеем право предположить, что каждый фотон рисует сразу всю картинку, только очень слабенькую. А с каждым новым фотоном вся эта картинка усиливается и усиливается!» И до сих пор пропагандируют эту чушь – о том, что фотон может размазываться на всю фотопластинку! А ведь точно известно, что фотопластинки состоят из микроскопических зёрнышек. И точно известно: чтобы это фотографическое зёрнышко сработало, в нём должна произойти фотохимическая реакция – а она происходит при приобретении необходимой энергии возбуждения, т.е. при поглощении фотона целиком! Неужели отсюда не ясно, что каждый фотон попадает в одну точку на фотопластинке? И неважно, обычный при этом световой поток, или сверхслабый! Просто в первом из этих случаев светлые и тёмные полосы получаются быстренько, а во втором – нужно долго ждать, пока они нарисуются. Из отдельных точек! Но это значит, что если фотонам присущи волновые свойства, то они присущи каждому фотону в отдельности. Тогда повторяем вопрос: каким образом фотон «чувствует» систему щелей, через которую он проходит? Ответа как не было, так и нет!

Или вот ещё – тоже замечательное волновое явление. В биноклях и фотоаппаратах широко используется т.н. просветлённая оптика – у которой, по сравнению с обычными линзами, меньше обратное отражение, и, соответственно, лучше пропускание. Известно, что нужно сделать, чтобы оптика получилась просветлённая – но её работа, в рамках концепции летящих фотонов, выглядит непостижимым чудом. На поверхность линзы, отражение от которой требуется уменьшить, наносят тонкое покрытие. Его толщина делается такой, чтобы, для света из желаемого спектрального диапазона, при отражениях волнового фронта от двух поверхностей – «воздух-покрытие» и «покрытие-линза» - разность фаз соответствовала нечётному числу полуволн, т.е. чтобы волны, отражённые от этих двух поверхностей, гасили друг друга. В результате, как известно, отражение и вправду уменьшается, а пропускание увеличивается. Но не гасят же здесь друг друга фотоны, отражённые от этих двух поверхностей – иначе каким чудесным образом они, после этого, перескакивали бы из отражённого потока в проходящий? Да и, кроме того, «погасить» друг друга могли бы лишь те фотоны, которые ещё до отражения имели бы определённую разность фаз – но, в условиях естественного освещения, фазы фотонов распределены случайно, а просветлённая оптика всё равно работает! Значит, опять же, каждый фотон должен индивидуально, независимо от других фотонов, попадать в проходящий поток! Но как фотон может это делать? Неужели он отражается от тех двух поверхностей сразу, из-за чего гасит сам себя и перескакивает из отражённого потока в проходящий? Или, ещё лучше: неужели он заранее знает, что, отразившись, он погасит сам себя, поэтому он не рискует и по-простому летит вперёд?

Бессилие концепции летящих фотонов применительно к этим простейшим волновым явлениям – просто поражает. Намучившись досыта неудачными попытками объяснить происхождение волновых свойств у фотонов, отчаявшиеся теоретики притянули эти свойства за уши, приписав каждому фотону «волновую функцию». Что это такое, они сами толком не понимают – даже после грандиозной дискуссии о её физическом смысле. Но, не требуя никакого понимания, волновая функция фотона позволяла описать и, какое хочешь, его размазывание по пространству, и ту же интерференцию. Правда, конфуз всё же вышел. Спрашивается: если фотон размазан по пространству, скажем, на пару десятков метров, как это описывает его волновая функция, то означает ли это, что и энергия фотона размазана на ту же пару десятков метров? Если не размазана, то все разговоры о волновой функции и её физическом смысле – это, извиняемся, просто трёп. А если размазана – то каким же дивным образом она схлопывается в точку при поглощении фотона фотографическим зёрнышком или светочувствительной клеткой глаза? Ответа на этот вопрос так и не выработали. Лишь придумали высоконаучный термин для такого схлопывания: «редукция волнового пакета». А как происходит эта «редукция» - не придумали. Ни ума не хватило, ни фантазии. А чтобы прикрыть своё бессилие, изобрели ещё один восхитительный термин: «корпускулярно-волновой дуализм». В переводе на общепонятный язык этот термин означает, что у фотона имеются свойства и частицы, и волны – но как они уживаются друг с другом, совершенно не ясно. Поэтому, если кто-то что-то недопонял про фотоны, то пусть предъявляет претензии не к теоретикам, а к корпускулярно-волновому дуализму. Главное, мол, к этому дуализму хорошо привыкнуть – и тогда, мол, будет полное понимание природы света!

Теперь самое время изложить альтернативу этому лепету официальной науки. По логике «цифрового» мира, световая энергия не движется по пространству между атомами – ни в виде волн, ни в виде фотонов – а перебрасывается непосредственно с атома на атом программными манипуляциями. Поскольку при распространении света нет физического посредника, переносящего энергию возбуждения с атома на атом, то нет и физического носителя свойств, приводящих к волновым эффектам при распространении света. По логике вышеизложенного, к этим волновым эффектам приводят особенности работы Навигатора (3.4), прокладывающего путь квантам энергии возбуждения атомов.

Что же это за особенности? Как отмечалось выше (3.4), Навигатор сканирует пространство вокруг возбуждённого атома в поисках атомов-адресатов, находящихся в тех местах, в которые вероятность квантового переброса энергии возбуждения оказывается максимальной. При этом Навигатор методично обрабатывает все имеющиеся разветвления путей волн расчётных вероятностей. Эти разветвления возникают там, где происходят нарушения невозмущённого движения «волнового фронта»: на отражающих и преломляющих поверхностях, на делительных пластинках, на различных препятствиях, дробящих «волновой фронт» - в частности, на той же системе параллельных щелей. Пусть разветвлённые пути волн расчётных вероятностей затем где-то пересекаются. В областях этих пересечений, по логике работы Навигатора, результирующие расчётные вероятности определяются наложением этих волн друг на друга. Таким образом, «интерферируют» именно волны расчётных вероятностей. В частности, светлые полосы на экране за системой параллельных щелей появляются на тех местах, для которых итоговые вероятности переброса квантов энергии возбуждения оказываются наибольшими. При этом лишён смысла вопрос о том, сквозь какую щель прошёл тот или иной квант, попавший в ту или иную светлую полосу на экране. Сквозь щели «проходили» волны расчётных вероятностей. А квант мог быть переброшен непосредственно с атома источника света на атом экрана – без прохождения по пространству между ними и, значит, без прохождения сквозь систему щелей. Это непривычно, но это реалии «цифрового» мира!

Здесь требуется важное уточнение. Для каждого возбуждённого атома работает индивидуальный канал Навигатора, который ищет атома-адресата только для этого возбуждённого атома. И «интерферировать» могут лишь те волны расчётных вероятностей, которые продуцируются одним и тем же каналом Навигатора, т.е. лишь те, с помощью которых устанавливается какая-то одна пара «атом-отправитель – атом-получатель». Сам принцип работы Навигатора основан на том, что расчёты вероятностей переброса для каждого кванта производятся независимо от расчётов для других квантов. Поэтому «интерференция» волн расчётных вероятностей в каждом канале Навигатора происходит независимо от работы других его каналов. Это и является причиной того, что пересекающиеся пучки света совершенно не мешают друг другу.

«Нет-нет, - скажут ортодоксы. – Это при слабых световых потоках они не мешают друг другу. Фотонов летит мало, вот они и не сталкиваются! А при мощных световых потоках фотоны рассеиваются друг на друге! Мы даже считаем сечения этого рассеяния!» Друзья, считать вы можете что угодно – до посинения. Но где вы видели рассеяние фотонов друг на друге? В фокусе лазерного луча, что ли – где возникает пробой воздуха и вспыхивает искра? Так там без вещества не обходится! А вот в сверхвысоком вакууме лабораторных установок – никаких подобных спецэффектов не наблюдается! Куда же при этом деваются способности фотонов рассеиваться друг на друге? Давайте, друзья, посерьёзнее!

Повторяем: учёт того, что различные каналы Навигатора работают независимо – для каждого кванта индивидуально – одним махом объясняет все волновые явления при распространении света. В том числе – те интерференционные явления, которые имеют место при сверхслабых световых потоках, когда кванты передаются поодиночке. У каждого кванта здесь имеется повышенная вероятность быть переброшенным в любую точку из тех мест, где получатся светлые полосы. Но попадёт он, конечно, в какую-то одну точку. И, лишь когда квантов перебросится достаточно много, светлые полосы станут заметны. Как можно видеть, тривиально устраняются парадоксы с «самоинтерференцией» одиночного фотона, с редукцией его волновой функции, и т.п.

О том, что всё это – правда, свидетельствует ещё одна тонкость в интерференции световых волн, которую наука тщательно скрывает. Вот у волн в вещественных средах – например, звуковых волн или волн на поверхности воды – есть характерная особенность. Эти волны, будучи порождаемы различными независимыми источниками, отлично интерферируют – тем лучше, чем лучше совпадают частоты вибраций их источников. Но мало кто знает, что в случае световых волн это не так: интерференции света от независимых источников нет, как бы здорово ни совпадали их спектральные линии. Даже – в случае лазерных источников света, когда их совпадающие спектральные линии являются исключительно узкими. Те, кто пытались получить интерференционную картинку, смешивая свет от двух однотипных лазеров (одночастотных!), мучились долго, упорно, и безуспешно. Желающие могут повторить. Только не сделайте ошибочку, подменяя интерференционную картинку биениями частот. Чтобы получить биения частот двух лазеров, долго мучиться не нужно: направляете лучи на достаточно быстродействующий фотодиод, и снимаете сигнал на разностной частоте. Этот сигнал получается оттого, что освещённость мордочки диода периодически изменяется. Мы же говорим об интерференционной картинке, которая, по определению, является статической [Л5] – например, статическая система светлых и тёмных полос – при которой изменений освещённости мордочки фотодиода нет. Казалось бы, чепуха какая-то – когда интерференция света имеет место, получаются великолепные статические картинки, как и положено! Нет, это не чепуха. Все без исключения интерферометры работают так: они расщепляют свет от одного и того же источника, прогоняют его по различным путям, а затем вновь сводят. Только так получаются световые интерференционные картинки! Да почему же? А потому, что каналы Навигатора для различных квантов работают независимо, и «интерферировать» могут лишь те волны расчётных вероятностей, которые порождаются одним и тем же каналом Навигатора. Вот почему интерференции света от различных независимых источников – даже лазерных – не может быть в принципе.

Как можно видеть, логика «цифрового» мира, в применении к явлениям интерференции света, даёт разумное и непротиворечивое устранение парадоксов, нагромождаемых ортодоксальным подходом.

Следует добавить пару слов ещё об одном ключевом волновом явлении при распространении света – дифракции. Это явление заключается в том, что у света, встречающего препятствия на своём пути, происходят соответствующие отклонения от прямолинейности распространения. Так происходит потому, что точки на краях препятствий становятся источниками вторичных волн, которые интерферируют с волнами, прошедшими рядом с краями. А об интерференции мы уже сказали выше.

Явление голографии является поразительной иллюстрацией работы Навигатора (3.4). Как и другие вышеназванные парадоксы – например, с просветлением оптики (3.5) – голография не имеет разумного объяснения ни на основе концепции световых волн, ни, тем более, на основе концепции фотонов. Напротив, на основе модели волн расчётных вероятностей (3.4) голография находит естественное объяснение.

Рассмотрим случай классической голографии, когда для записи голограммы используется прозрачная пластинка с тонким фото-слоем. Источник света для записи голограммы должен обеспечивать достаточно высокую когерентность – для получения качественной интерференционной картинки – поэтому здесь обычно используются лазерные источники света. На стадии записи голограммы, расширенный пучок света расщепляется делительной пластинкой Д (см. Рис.3.6.1) на два. Один из них направляется на фотопластинку Ф прямо (т.н. опорный пучок), а второй (т.н. предметный пучок) освещает объект О так, чтобы на фотопластинку попадал свет, рассеянный на объекте О. На фотопластинке получается картинка интерференции опорного и предметного пучков – это и есть голограмма. Для понимания того, как она воспроизводит образ объекта, следует понимать, по какому принципу оказались выбраны те места на фотопластинке, в которых фотографические зёрнышки сработали и создали т.н. точки почернения.

Рис.3.6.1

Как мы излагали выше (3.5), каждому кванту света прокладывает путь отдельный канал Навигатора. При этом обрабатываются все имеющиеся варианты движения волн расчётных вероятностей (3.4) – отчего создаётся иллюзия вариантов путей, по которым может лететь квант, чтобы попасть на фотопластинку. На наш взгляд, «варианты путей» имеются лишь для волн расчётных вероятностей, а квант отнюдь не «летит»: по завершении расчётов в своём канале Навигатора, квант почти-мгновенно (3.3) перебрасывается в ту точку на фотопластинке, для которой расчётная вероятность переброса оказалась максимальной. Для каждого кванта такая точка на фотопластинке – своя; но положения этих точек для множества квантов определяются одним и тем же принципом. Этот принцип очень прост, если иметь в виду, что продольный профиль волны расчётных вероятностей представляет собой последовательность узких пиков (3.4), следующих друг за другом с интервалами в одну длину волны. Так вот: точки максимально вероятного попадания кванта – это те точки на фотопластинке, в которых волны расчётных вероятностей (опорного и предметного пучков) схлёстываются своими пиками. Ещё раз подчеркнём: каждому кванту соответствует множество точек на фотопластинке, где волны расчётных вероятностей схлёстываются своими пиками, но попадает квант только в одну из таких точек, и только в ней происходит результирующее срабатывание фотографического зёрнышка. При достаточной величине экспозиции, даже в элементарном случае точечного объекта, на фотопластинке получится система точек почернения – интерференционная картинка. В случае объекта более сложного, чем точечный, каждой его точке, от которой рассеянный свет попадает на фотопластинку, будет соответствовать своя система точек почернения, т.е. своя интерференционная картинка на результирующей голограмме.

В этой процедуре записи голограммы не происходит, казалось бы, ничего удивительного. Но далее, на стадии воспроизведения, происходит настоящее чудо – если подходить к происходящему в рамках традиционных представлений о свете. Голограмму освещают только одним пучком света – опорным, повторяя геометрию его падения на стадии записи (Рис.3.6.2). Этот свет, падающий на голограмму, дифрагирует на её точках почернения, каждая из которых оказывается в роли «источника вторичных волн». В результате свет, прошедший сквозь голограмму, формирует мнимое изображение объекта – которое, при хорошем качестве голограммы, визуально неотличимо от оригинала. Сказать, что изображение объекта получается объёмное – это почти ничего не сказать. Дело в том, что при изменении, в некоторых пределах, угла зрения, объект предстаёт в соответственно изменяющихся ракурсах, т.е. наблюдатель может «заглянуть за край» изображения!

Рис.3.6.2

Эти колоритные особенности голографического изображения поясняются во многих учебниках тем, что, на стадии записи, на фотопластинке записывается информация не только об амплитудных соотношениях интерферирующих волн, но и об их фазовых соотношениях – а, при воспроизведении, эти фазовые соотношения, якобы, тоже воспроизводятся. Такое пояснение, лишь из вежливости, сгодится в качестве поэтической метафоры – ибо, физически, оно бессмысленно. Причина совсем проста: зрительный аппарат человека не производит фазового детектирования входящего света, он обрабатывает лишь попадания квантов в светочувствительные клетки сетчатки.

Но голографическое изображение, в рамках традиционных представлений о свете, является чудом не только потому, что если даже фазовые соотношения как-то записывались бы на голограмме, то они были бы совершенно бесполезны при визуальном восприятии записанного изображения. Дело ещё вот в чём. Интерференция и дифракция являются волновыми явлениями, поэтому феномен голографии пытаются объяснять в терминах световых волн, продольный профиль которых представляет собой синусоиду. Для простейшего случая точечного объекта, этот подход работает. Синусоидальная волна, дифрагируя на интерференционной картинке, которая соответствует точечному объекту, действительно сформирует мнимое изображение этого точечного объекта – что в теории дифракции доказывается строго математически. Но на этом в учебниках и заканчивается объяснение феномена голографии. А такого «объяснения» совершенно недостаточно! В самом деле, пусть объект представляет собой всего-то две различные точки, каждой из которых будет соответствовать своя система точек почернения на записанной голограмме. Опорная синусоидальная волна, падая на такую голограмму, будет дифрагировать сразу на обеих названных системах точек почернения, поскольку отсутствует какой-либо механизм, обеспечивающий селективную дифракцию – только на той или только на другой системе точек. Поэтому никаких изображений двух точек объекта не будет сформировано: световые волны, которые сформировали бы эти изображения по отдельности, «тупо» проинтерферируют друг с другом и создадут в итоге визуальную какофонию. От этого случая двухточечного объекта ничем принципиально не отличается случай, когда объект состоит из множества различных точек. Таким образом, из традиционных представлений о свете прямо следует, что голографические изображения обычных объектов не могут формироваться в принципе.

Но ведь они формируются, да ещё как! В чём же разгадка этого чуда? Разгадка, на наш взгляд, в том, что световых волн не существует в природе, а голографические изображения формируются с помощью волн расчётных вероятностей. Напомним, что эти волны имеют не физическую природу, а чисто программную (3.4) – и, когда мы говорим о дифракции и интерференции этих волн, мы подразумеваем, что эти явления происходят на программном уровне реальности. Результат дифракции волны расчётных вероятностей на голограмме будет отличаться от результата дифракции световой синусоидальной волны – вторичные волны которой, интерферируя, тотально суммировались бы друг с другом. У вторичных волн расчётных вероятностей, сразу после дифракции на голограмме, интерференция поначалу тоже имеет характер тотального суммирования. Но Навигатор быстро обнаруживает, что среди всех имеющихся вариантов наложения пиков вторичных волн начинают устойчиво выделяться те варианты, для которых вероятности переброса кванта заметно выше средней шумовой величины (кстати, расчёты, производимые Навигатором, чрезвычайно упрощаются благодаря дискретному характеру волн расчётных вероятностей). Каждый устойчиво выделяющийся вариант – это результат наложений пиков только тех вторичных волн, источниками которых являются точки почернения на голограмме, соответствующие какой-то одной точке объекта! Теперь учтём, что Навигатор начинает просчитывать все возможные варианты переброса кванта, но, отбрасывая маловероятные из них, продолжает просчитывать лишь наиболее вероятные – поэтому, например, исходящая из атома первичная сферическая волна, дойдя до первых же атомов, приобретает уже лучевую направленность, и т.д. (3.4). Этот феномен мы называем приоритетной интерференцией. Возвращаясь к дифракции опорного пучка света на голограмме, мы замечаем, что, благодаря приоритетной интерференции, Навигатор будет просчитывать до конца лишь те варианты переброса кванта, которые, на стадии воспроизведения, дадут иллюзию «прямого полёта» кванта от той или иной точки объекта. Совместное восприятие таких квантов и даст голографическое изображение объекта.

Как можно видеть, именно приоритетная интерференция вторичных волн расчётных вероятностей при работе Навигатора обеспечивает независимое воспроизведение образов различных точек объекта – в противоположность визуальной какофонии, неизбежной по концепции обычной, тотальной интерференции световых волн. Именно с учётом приоритетной интерференции легко объясняются необычные особенности голографического изображения, например, изменение его ракурса при соответствующем изменении угла зрения. Действительно, голограмма содержит интерференционные картинки, соответствующие всем точкам объекта, от которых рассеянный свет попадал на фотопластинку при записи – в том числе и от тех точек, которые видимы при несколько различающихся ракурсах. Поскольку, при воспроизведении голографического изображения, создаётся иллюзия «прямого полёта» квантов от той или иной точки объекта, то кванты «от точек, прикрытых краем изображения», «не попадают» в глаз, но начинают попадать в него при соответствующем его перемещении – что и создаёт полную иллюзию «заглядывания за край».

Аналогично, с учётом приоритетной интерференции объясняется тот феномен, что на одной фотопластинке можно записать несколько наложенных друг на друга различных голограмм – и каждая из них, при освещении фотопластинки соответствующим опорным пучком, будет успешно воспроизводить своё голографическое изображение. Более того, эти наложенные друг на друга голограммы могут быть получены при различных длинах волн у опорных пучков – что делает возможным феномен цветной голографии.

Наконец, с учётом приоритетной интерференции объясняется свойство голограммы, которое обычно производит самое сильное впечатление: фрагмент фотопластинки, на которой была записана голограмма, воспроизводит весь голографический образ – правда, с соответственно пониженными резкостью и контрастностью. Так и должно быть: в случае с фрагментом, изображение формируется с помощью меньшего количества точек почернения, но принципы-то его формирования – те же самые, что и при работе всей площади фотопластинки!

Исторически сложилось так, что радиоволны открыли, когда световые явления были уже довольно хорошо изучены, и когда уже имелась теория Максвелла, которая описывала световые волны как упругие волны в эфире, распространявшиеся в нём с характеристической скоростью c. Когда обнаружилось, что скорость радиоволн совпадает с этой скоростью [Ф2], то на радостях решили, что свет и радиоволны имеют одну и ту же физическую природу, различаясь лишь по своим диапазонам частот. До сих пор в учебниках и справочниках фигурирует «шкала электромагнитных волн», которая охватывает все мыслимые частоты – от нуля до бесконечности. Такое положение дел тем более удивительно, что уже давно известны прямые указания на принципиально разную природу света и радиоволн.

Главное различие между ними в том, что свет – это квантовая передача энергии, а радиоволны – волновая. Заметьте, мы говорим о физической сути этих явлений, а не об их математическом описании. Математически – и свет, и радиоволны можно описать как в терминах волн, так и в терминах квантов: бумага всё стерпит. А физически – есть большая разница. При излучении, распространении и приёме радиоволны возможны подвижки заряженных частиц на частоте волны. Сколь долго работает генератор, непрерывно гоняющий заряды по излучающей антенне, столь же долго трепыхаются заряженные частицы в окружающем пространстве. В случае же со светом, никаких подвижек заряженных частиц на световой частоте – не бывает. Откуда им быть, если механизм передачи энергии совершенно другой? Кстати, даже электрон, со своей малой массой, не мог бы, будучи свободным, колебаться на световых частотах из-за своих инертных свойств. Поначалу полагали, что на такое способны электроны, связанные в атомах – например, согласно модели атома Дж.Дж.Томсона. Но от этой модели отказались в пользу модели Резерфорда-Бора… оформилась концепция фотонов… которые, согласно постановлению Первого Сольвеевского конгресса, излучаются и поглощаются атомами мгновенно. Отсюда следовало, что в атомах никаких колебаний заряженных частиц, задающих частоту фотона, не существует. Видите, к чему пришли сами ортодоксы: в случае радиоволн колебания заряженных частиц есть, а в случае света – нет. Но продолжали приписывать радиоволнам и свету одну и ту же физическую природу. Чтобы было загадочней!

А ведь эта разница между наличием или отсутствием колебаний заряженных частиц обусловлена не просто различием частотных диапазонов – в данном случае, это вопрос принципиальный [Г10]. Навигатор, работу которого мы обрисовали выше (3.4), обслуживает только квантовые перебросы энергии, а именно, перебросы квантов энергии возбуждения с атома на атом, но уж никак не с электрона на электрон. Потому что объект, способный приобрести и отдать энергию возбуждения, должен иметь соответствующую структурную организацию, которая обеспечивает внутреннюю степень свободы, допускающую саму возможность энергии возбуждения. А у свободного электрона, который является элементарной частицей, такой внутренней степени свободы нет. Поэтому электрон не может приобрести квант энергии возбуждения и, соответственно, не может отдать его.

Сказанного достаточно для осознания того, что свет и радиоволны – это принципиально различные физические феномены. К вопросу о природе радиоволн мы вернёмся ниже (5.3), а сейчас заметим следующее. При сравнении традиционных представлений о свете, как о летящих фотонах, и наших представлениях о нём, как о цепочке квантовых перебросов энергии возбуждения с атома на атом, бросается в глаза их принципиальное различие. В традиционном подходе свет, «выплюнутый» веществом, имеет самодостаточное, независимое от вещества существование: фотон, якобы, способен пролететь в межзвёздном пространстве длинные световые годы, пока не наткнётся на атом, который его поглотит. В нашем же подходе, света в отрыве от вещества не существует, т.к. световая энергия локализована только на атомах, и, при квантовых перебросах с одного атома на другой, она не движется по разделяющему атомы пространству. И вот, раз уж академики зачислили фотон в четвёрку фундаментальных, абсолютно стабильных частиц, то у академиков, в защиту представлений о независимом от вещества существовании фотонов, имеется трогательный мысленный эксперимент. Пусть, дескать, в десяти световых годах от нас сгенерировали мощную вспышку света, после чего излучатель сразу демонтировали… а приёмник мы еле успели построить к концу десятого года – но световой сигнал всё же приняли. Где же, дескать, находилась световая энергия все эти десять лет, когда излучателя уже не было, а приёмника ещё не было? Отвечаем: световая энергия перебрасывалась с атома на атом в межзвёздном пространстве, продвигаясь к строящемуся приёмнику. «Тогда, - торжественно восклицают академики, - предельная интенсивность пропускаемого света определялась бы концентрацией атомов, по которым он «перебрасывается»! Чем меньше была бы эта концентрация, тем хуже пропускался бы свет! А это не так: в лабораториях мы пропускаем сквозь сверхвысокий вакуум лазерные интенсивности!» Да, в лабораториях это получается. Но получается потому, что здесь объёмы со сверхвысоким вакуумом невелики: для атомов-отправителей, находящихся на входном окошке вакуумной камеры, Навигатор успешно находит атомов-получателей на её выходном окошке или на мишени внутри неё. Здесь «лазерная интенсивность» пропускается сквозь короткий участок со сверхвысоким вакуумом так, словно этого участка и нет вовсе. Но если участок со сверхвысоким вакуумом имел бы достаточно большую протяжённость, то всё происходило бы по-другому. Нам представляется логичным, что у Навигатора задан некоторый предельный радиус сканирования пространства в поисках атома-получателя. Если, по достижении этого предельного радиуса, атом-получатель не обнаруживается, то сканирование завершается (и, возможно, сразу же начинается его новый цикл). Тогда, при достаточно большой протяжённости участка пути света сквозь высокий вакуум, именно малая концентрация вещества должна служить ограничителем пропускной способности света этим участком.

И, в самом деле, имеются свидетельства о том, что на космических просторах всё происходит именно так. Почему, например, постоянна «солнечная постоянная», т.е. мощность солнечного излучения, приходящаяся на единичную площадку на радиусе орбиты Земли? Ведь даже в годы активного Солнца, при повышенном пятнообразовании и соответствующем увеличенном выходе энергии наружу, названная мощность, практически, не изменяется [С5]. Этот феномен стабилизации мощности излучения Солнца обычно пытаются объяснить каким-либо присущим Солнцу механизмом автоматического регулирования. Трудно поверить в такой механизм, глядя на видеосъёмки поверхности Солнца: эта поверхность бурлит и извергает чудовищные протуберанцы. Энергия так и рвётся наружу, но что-то её сдерживает. И нам представляется правдоподобной версия о том, что «поток электромагнитной энергии, приходящий от Солнца, стабилизируется ограниченными пропускными способностями сильно разреженной космической среды» [К5]. Будь концентрация атомов в межпланетном пространстве на порядок больше – Солнышко нас сожгло бы. Вот, смотрите: когда большая комета проходила между Солнцем и Землёй и достаточно сильно «газила», её хвост, направленный от Солнца, формировал створ с повышенной концентрацией вещества. Через этот створ Солнце припекало Землю сильнее, чем обычно, что вызывало всплеск климатических аномалий и стихийных бедствий. Похоже, что идущая из глубины веков слава о кометах, как о предвестниках несчастий и катаклизмов, основана не на суевериях, а на реальных причинно-следственных связях.

Но эта история – так сказать, дела давно минувших дней. А есть ли что-нибудь посовременнее, с переднего края науки и техники? А как же! Это – поучительная история о том, как позорно провалилась затея поражать лазерными лучами космические объекты. Ведь сделали образцы боевых газодинамических лазеров, которые прожигают броню и сшибают крылатые ракеты. Правда, это у них получается вблизи поверхности Земли, в условиях стандартной атмосферы. Если исходить из концепции летящих фотонов, то в космосе эти лазеры должны справляться с боевыми задачами ещё лучше. Ан нет. Это только в фильмах и компьютерных играх, фабрикуемых по тематике «звёздных войн», космические корабли в клочья разносятся лазерными лучами. А в реальности оказывается, что лазерный луч, который сквозь воздух прожигает броню, в космосе едва справляется со смехотворной задачей: выведением из строя светочувствительных элементов у спутника-шпиона. Помните, дорогой читатель, был период, когда в средствах массовой информации центральной темой была тема про Стратегическую оборонную инициативу США (СОИ)? Говорили-говорили про эту инициативу, а потом вдруг – раз! – и всё моментально стихло. А позже по центральному телевидению, в программе «Время», прошёл коротенький сюжет: на показательных испытаниях космического боевого лазера, попавший под его луч макет боеголовки и вправду разнесло в клочья – но это оттого, что бравые американские вояки предусмотрительно установили в нём взрывное устройство, и в нужный момент нажали на кнопочку. По-честному у них не получалось: что-то мешало боевым фотонам лететь в космическом вакууме так же лихо, как и вблизи поверхности Земли. Кстати, вопрос о том, почему боевые лазеры не оправдали надежд в космосе, поднимался на специализированных форумах в Интернете. И, знаете, такую постановку вопроса воспринимали серьёзно! Толпа адвокатов начинала отвечать на этот вопрос, изобретая причины получившейся неудачи. Вот, например, одна из их придумок: боеголовка в полёте, видите ли, вращается, поэтому лазерное пятно перемещается по её поверхности, вот лазер её и «не берёт». Ну, прямо незадача: склепали стратегический оборонный лазер, вывели его в космос… и всё рухнуло к чёртовой матери! Никто на переднем крае науки и техники не мог предвидеть, что боеголовка в полёте вращаться будет!

Вот и верь после этого академикам, что они «пропускают сквозь сверхвысокий вакуум лазерные интенсивности»! В космосе-то, к изумлению академиков, это не получается. Но нельзя же им признаваться в том, что они совершенно не понимают, что такое свет!

Как мы излагали выше (1.6), иерархия частотных воронок задаёт систему разграниченных в пространстве областей «инерциальной привязки» для механических явлений. В частности, по отношению к местному участку частотного склона определяется локально-абсолютная скорость тела, которая имеет чёткий физический смысл: от квадрата именно этой скорости зависит «истинная» кинетическая энергия тела, которая участвует в тех или иных превращениях энергии – всегда происходящих однозначно (1.6).

Уместен вопрос: а задана ли «инерциальная привязка» для скорости распространения света? Мы отвечаем на этот вопрос утвердительно. И нам представляется, что принцип, по которому организована «инерциальная привязка» для скорости света, совпадает с тем, по которому она организована для локально-абсолютных скоростей физических тел. А именно: фазовая скорость света, т.е., в нашей модели, скорость продвижения «поисковых волн» при работе Навигатора (), является изотропной константой c по отношению к местному участку частотного склона. Из этого принципа следуют все остальные наблюдаемые проявления поведения скоростей света. Мы говорим «скоростей», потому что кроме фазовой скорости, с которой продвигается «поисковая волна» по пространству, у света есть ещё групповая скорость, с которой продвигается световая энергия – по цепочке атомов.

Смотрите: в случае упругой волны – например, звуковой – её скорость определяется упругими свойствами вещественной среды, поэтому скорость волны «привязана» к этой среде. Так, если звук распространяется в ламинарном потоке жидкости, текущем по трубе, то звук «сносится» этим потоком, и скорость звука относительно трубы равна сумме скорости потока жидкости в трубе и скорости звука в покоящейся жидкости. Что же касается «поисковой волны», то она является не физической реальностью, а программной, и скорость её продвижения в пространстве между атомами никак не «привязана» к этим атомам. Стартовав с атома-отправителя, «поисковая волна» движется со скоростью, которая определяется лишь быстродействием работы Навигатора, причём скорость этой «программной» волны привязана к программной же реальности – местному участку частотного склона, задающего инерциальный фон. Поведение же скорости продвижения кванта световой энергии по цепочке атомов – это следствие поведения скорости «поисковой волны». При том, что перебросы кванта энергии возбуждения с атома на атом осуществляются программными манипуляциями, практически, мгновенно (3.4) – результирующая скорость продвижения этого кванта по цепочке атомов, разумеется, конечна: квант света никоим образом не обгонит передний фронт «поисковой волны» своего канала Навигатора. В итоге оказывается, что из «привязки» скорости «поисковой волны» к местному участку частотного склона вытекает видимость аналогичной «привязки» для скорости продвижения светового кванта по цепочке атомов. И, по мере уменьшения концентрации атомов, видимость идентичности поведения этих двух скоростей становится выражена всё ярче. На этой-то видимости, как нам представляется, и держится вывод теоретиков о том, что в вакууме фазовая и групповая скорости света совпадают. Правда, фазовую и групповую скорости света теоретики понимают в традиционном смысле – как скорость движения горбов монохроматической световой волны и скорость движения светового импульса – но суть от этого не меняется.

И тут обнаруживается нечто интересное. Говоря о фазовой или групповой скорости света в вакууме, теоретики умалчивают, по отношению к чему подразумевается эта скорость. Они полагают, что имеют на это право – благодаря принципу относительности, (первому постулату СТО), из которого, применительно к «скорости луча света в пустоте», следует одинаковость этой скорости для всех наблюдателей, «движущихся друг относительно друга равномерно и прямолинейно». Причём, утверждается, что такое поведение скорости света имеет место на опыте: в каких только направлениях не двигались земные лаборатории, а для скорости света в вакууме измеряли одно и то же значение. Это – коронный номер теории относительности: свет, мол, движется с одной и той же скоростью для всех! «Как такое возможно?» – спрашивают релятивистов. – «А вот так! – веселятся они. – Это не каждому дано понять!»

Ну, ну, не расстраивайтесь, дорогой читатель! Нет тут особых сложностей для понимания – надо только знать, в чём секрет фокуса. Нормальный человек под «скоростью» понимает скорость движения в одном направлении – идеализацией такого подхода является понятие «мгновенная скорость». А в экспериментах, где обнаруживалась скорость света, «одинаковая для всех», непременно использовались интерферометры или резонаторы, в которых свет бегал «туда-сюда» [Г11]. Т.е., в этих экспериментах измерялась скорость света не «в один конец», а «туда-обратно». Но это же – совсем разные вещи! Пусть прибор имеет ненулевую локально-абсолютную скорость V, т.е. движется с этой скоростью относительно «инерциального фона», задающего привязку для скорости света. Тогда в этом приборе скорость света «в один конец» будет анизотропна: по ходу движения прибора она будет равна c-V, а, против хода, c+V. Но, при измерении скорости света «туда-обратно», вклады от положительной и отрицательной поправочек скомпенсируют друг друга. В этом и заключается секрет фокуса! Вообще-то, компенсация поправочек здесь получится не совсем в ноль: малая остаточная разность, ~(V/c)², должна иметь место. И это, в самом деле, обнаруживается на опыте – чем прямо опровергается принцип относительности. Как уже отмечалось выше (1.7), даже Майкельсон и Морли обнаружили квадратичный эффект, где в качестве скорости V фигурировала локально-абсолютная скорость прибора – на местный восток, из-за участия в суточном вращении Земли. А нам вдалбливали, что, поскольку у Майкельсона и Морли не проявилось орбитальное движение Земли, то результат их опыта был нулевой – в согласии, мол, с принципом относительности! Это нам врали – про «нулевой результат» и про «согласие». Проявлению орбитального движения Земли там было неоткуда взяться: на склонах земной частотной воронки, инерциальная привязка для скорости света задана независимо от того, как эта воронка движется – и движется ли она вообще. А вот локально-абсолютная скорость прибора при этом вполне детектируется – что получилось не только у Майкельсона-Морли, но и, например, у Брилета и Холла (1.7). И детектируется она именно потому, что в оптическом приборе скорость света «в один конец» является классической суммой двух локально-абсолютных скоростей – у света и у прибора! Как можно видеть, «скорость света в понимании нормального человека», т.е. скорость света «в один конец», оказывается отнюдь не одинакова для всех. Для каждого из этих «всех» она определяется индивидуально, в соответствии с его вектором скорости, через классическую сумму скоростей – как и следовало ожидать при не свихнувшемся рассудке. Это – экспериментальные реалии, убийственные для принципа относительности.

Впрочем, не менее убийственен для принципа относительности даже такой феномен, как линейный эффект Допплера в оптике. Пока свет считали упругими волнами в эфире, допплеровские сдвиги длин волн, при движении в эфире излучателя и приёмника, объяснялись тривиально. Упразднив эфир, а заодно и скорости излучателя и приёмника по отношению к нему, Эйнштейн заявил, что линейный эффект Допплера в оптике зависит лишь от относительной скорости излучателя и приёмника – скорости их сближения или расхождения. Откуда же, при таких делах, могут браться допплеровские сдвиги длин волн – да ещё если, согласно принципу относительности, скорость света всегда одинакова как для излучателя, так и для приёмника? Релятивисты этого сами не понимают: кроме абстрактных математических вывертов с четырёх-векторами, никакого физического объяснения у них нет.

По нашей же модели «привязки» скорости света – здесь всё прозрачно для понимания. Если атом-источник движется относительно локального участка частотного склона, т.е. имеет ненулевую локально-абсолютную скорость, то каждая последующая «поисковая волна» будет расходиться из нового центра, так что длина волны, идущей по ходу движения источника, будет уменьшена, и наоборот – в согласии с выражением для линейного эффекта Допплера. Аналогично, атом-получатель, из-за своего движения, также будет воспринимать изменённой длину «поисковой волны». Подчеркнём, что наличие линейных допплеровских сдвигов длин «поисковых волн» отнюдь не означает, что это отразится на величинах передаваемых квантов энергии. Прямые доказательства изменения энергии кванта света из-за движения атома-источника или атома-приёмника – отсутствуют. И если допустить, что этого изменения энергии действительно нет, то для нас сразу проясняется вопрос о том, каким же образом соблюдается закон сохранения энергии при квантовой передаче, сопровождаемой линейным эффектом Допплера. Традиционно, соблюдение этого закона здесь пытаются объяснить с учётом эффекта отдачи при излучении и поглощении фотона. Но это объяснение – из разряда противоречивых, поскольку отдача имела бы место даже у покоящегося атома-источника, когда допплеровского сдвига на нём нет! Проблема устраняется, если допустить, что линейные допплеровские сдвиги испытывают лишь длины «поисковых волн», и это не отражается на энергиях квантов света.

Добавим, что имеют место годичные вариации положений спектральных линий звёзд – в соответствии с орбитальным движением Земли вокруг Солнца [С2]. Мы объясняем это тем, что «поисковые волны» приобретают сдвиги, эквивалентные допплеровским, при пересечении «подвижной» границы раздела двух различных областей «инерциальной привязки»: длина волны изменяется при входе в частотную воронку Солнца, а затем – при входе в частотную воронку Земли. Но наблюдаемый цвет звезды при этом не должен изменяться. Так ли это в действительности – однозначный ответ нам неизвестен. Ситуация осложняется тем, что сдвиги спектральных линий звёзд могут иметь не только допплеровское происхождение [Г12].

Заметим, что из «привязки скорости света» к местному участку частотного склона немедленно следует независимость скорости света от характера движения источника – хорошо известное явление, которое у Эйнштейна не объясняется, а лишь постулируется (второй постулат СТО). Здесь, конечно, подразумевается скорость света «в один конец» - в частности, света, идущего от двойных звёзд к земному наблюдателю. Видимое обращение двойных звёзд отличалось бы от кеплеровского, если бы свет от приближавшейся к нам звезды двигался быстрее, чем от удалявшейся.

Добавим, что, благодаря орбитальному движению планетарных частотных воронок, возможно наблюдать такой феномен, как полное увлечение света планетарным «инерциальным пространством» - если пустить световой импульс так, чтобы он прошёл планетарную воронку насквозь, параллельно вектору её орбитальной скорости. Двигаясь по межпланетному пространству до влёта в планетарную частотную воронку и после вылета из неё, световой импульс имел бы скорость c по отношению к солнечному частотному склону. В пределах же планетарной частотной воронки, он имел бы скорость c по отношению к ней самой – а она, в свою очередь, движется относительно солнечного частотного склона с орбитальной скоростью. Тогда полётное время светового импульса, проходящего сквозь планетарную частотную воронку по ходу её орбитального движения, было бы меньше полётного времени импульса, проходящего по тому же самому пути в обратном направлении. Например, для случая земной частотной воронки, имеющей радиус R?900000 км, полётные времена световых импульсов, которыми обменивались бы космические корабли, находящиеся за её пределами, могли бы различаться на величину ~4RV_orb/c², где V_orb=30 км/с, т.е. примерно на одну миллисекунду.

Как можно видеть, эйнштейновская процедура синхронизации часов с помощью световых импульсов, движущихся «туда и обратно», могла бы, теоретически, быть корректна лишь в пределах одной и той же области «инерциального пространства» - например, в области планетарного тяготения. Ведь при пересечении светом границы этой области, переключается «привязка» его скорости, и пролётные времена «туда» и «обратно» перестают быть равными.

Уместно добавить, что ситуация совершенно аналогична и для случая радиоволн, «привязка» скорости которых организована по тем же принципам, как и для скорости света. Мало кто знает, что, на XVII Генеральной конференции по мерам и весам в 1983 г., константе c, т.е. «скорости плоской электромагнитной волны в вакууме», было приписано значение с нулевой погрешностью: c=299792458 м/с [Д3]. Это понадобилось для того, чтобы без ущерба перенести точность частотных измерений на измерения длин, и, таким образом, реализовать «пролётное определение метра»: это расстояние, проходимое плоской электромагнитной волной в вакууме за время, равное 1/299792458 секунды. На этом «пролётном определении метра» и основана работа спутниковых навигационных систем – в частности, GPS. Но, из вышеназванных особенностей «привязки» скорости радиоизлучения следует, что корректное создание «навигационного поля» по принципам, реализуемым в GPS, возможно в пределах лишь одной и той же области тяготения – например, в пределах земной частотной воронки – когда используемые радиоимпульсы не пересекают её границ.

Традиционные представления о свете, как о летящих фотонах, подразумевают, что фотоны являются полноценными частицами, которые подвержены действию тяготения. Т.е., фотон, пролетающий вблизи массивного тела, должен искривлять свою траекторию из-за гравитационного притяжения к «силовому центру». Эйнштейн утверждал, что, помимо этого гравитационного притяжения, существует ещё один механизм, дополнительно искривляющий траекторию пролетающего фотона (см., например, [Э1]). Согласно общей теории относительности (ОТО), по мере приближения к «гравитирующему телу», замедляется темп течения времени, и, соответственно, уменьшается скорость света. А известно, что градиент скорости света вызывает рефракцию, т.е. искривление траектории света в ту сторону, где его скорость меньше. Предсказанная величина поворота траектории фотона из-за этой «гравитационной рефракции» оказалась такая же, как и из-за чисто гравитационного притяжения фотона, т.е. теория Эйнштейна предсказывала удвоенное искривление луча, по сравнению с классическими предсказаниями. Если на опыте обнаружился бы удвоенный эффект – это подтвердило бы общую теорию относительности.

Такие опыты были проведены; но прежде чем о них говорить, изложим предварительные соображения, следующие из наших представлений о свете. Во-первых, фотонов, в традиционном понимании, не существует: кванты световой энергии перебрасываются непосредственно с атома на атом, не проходя по разделяющему атомы пространству (3.4). Раз нет летящих фотонов, то нет и гравитационного воздействия на них. Направление продвижения кванта света определяется только Навигатором (3.4), в работу которого тяготение не вмешивается. Во-вторых, сегодня можно считать твёрдо установленным, что имеют место гравитационные сдвиги квантовых уровней энергии в веществе, но они обусловлены отнюдь не «гравитационным замедлением времени» - которого не существует в природе (1.14), а, значит, не существует и зависимости скорости света от гравитационного потенциала, которая вызывала бы «гравитационную рефракцию». Таким образом, мы не усматриваем причин ни для действия тяготения на сам свет, ни для «гравитационной рефракции».

Но нас уверяют, что астрономам удалось обнаружить искривления лучей света от звёзд, проходившего вблизи Солнца – в согласии с предсказаниями ОТО! Оказалось, что эти уверения гроша ломаного не стоят. Астрономы, действительно, развернули бурную деятельность – но при этом они упорно выдавали желаемое за действительное.

Особенно на этом поприще отличился Эддингтон в 1919 г. Идея опыта заключалась в том, чтобы сфотографировать участок звёздного неба в окрестностях Солнца и сравнить его с опорной фотографией – того же участка, но в отсутствие Солнца. Искомый эффект заключался бы в соответствующих радиальных смещениях изображений звёзд – от Солнца. Но чтобы звёзды в окрестностях Солнца были заметны, съёмку следовало проводить в условиях полного солнечного затмения – ради чего и была организована астрономическая экспедиция.

Вся эта затея была изначально бессмысленна по совсем простой причине – узнавая о которой, сегодняшние релятивисты впадают в ступор. Дело в том, что, при съёмках неба в окрестностях Солнца, свет от звёзд проходил сквозь солнечную корону – неоднородную нестационарную среду – и испытывал при этом непредсказуемую рефракцию на неоднородностях плотности вещества, отчего изображения звёзд на фотопластинке могли смещаться на произвольные величины в произвольных направлениях. Совершенно ясно: ловить было нечего. Но даже если бы Эддингтону сказочно повезло, и, на время его наблюдений, вместо неспокойной плазмы солнечной короны имел бы место межпланетный вакуум, то и тогда его фотографии ровным счётом ничего не доказали бы – ввиду катастрофически недостаточной точности измерений.

Действительно, в замечательной статье [И1], написанной специалистом по практической астрономии, дан анализ погрешностей в эксперименте Эддингтона. По Эйнштейну, ожидаемая величина отклонения луча составляла 1.7 угловых секунды при пролёте света впритирку с краем Солнца. При пролёте на двух солнечных радиусах – ожидаемый эффект в два раза меньше, на трёх радиусах – в три раза меньше, и т.д. Из-за засветки прилегавшей к Солнцу области, реально наблюдались звёзды, находившиеся на небесной сфере на удалениях от 2 до 8 радиусов Солнца от его центра, при этом ожидаемый эффект составлял от 0.8 до 0.2 угловых секунд. По классическим представлениям, эффект был бы ещё в два раза меньше. «Основной целью экспедиции было опровергнуть теорию Ньютона и подтвердить теорию Эйнштейна. Следовательно, в данном эксперименте точность измерения должна была быть менее 0.1", что даже сейчас является фактически недостижимой задачей для наземных астрометрических измерений» [И1].

В самом деле, на выездной астрономической экспедиции мог использоваться только широкоугольный телескоп, с малым диаметром зеркала, а. значит, и с малым угловым разрешением. «Теоретическое значение кружка рассеяния для 300 мм телескопа равно 0.8"», а в реальности, из-за недостатков оптической системы, «угловой диаметр пятна рассеяния должен был составлять не менее 2 - 2.5", что в 3 раза превышало максимальную измеряемую величину» [И1]. Неидеальность гидирующего механизма должна была дать дополнительное размывание кружка рассеяния – минимально, на несколько десятых угловой секунды. Впечатляет и погрешность из-за зернистости фотопластинок. При поле зрения телескопа 4х4 градуса и стандартном размере пластинки, 18х24 см, «1 угловая секунда соответствовала 13 микронам на пластинке» [И1]. В 1919 г. «реальный размер зерна был порядка 20 - 30 микрон, а полученные "изображения" звезд представляли собой одно или два засвеченных зерна» [И1]. При этом ошибка определения положения звезды составляла, как минимум, одну угловую секунду. В довершение ко всему этому, Эддингтон наделал ещё и методологических ошибок, самой непростительной из которых считают вот какую. «Опорная фотопластинка была снята в январе в Англии (угол эклиптики над горизонтом - 20 град.), а затмение снималось на экваторе в 13:30, т.е. Солнце было в зените» [И1]. Атмосферная рефракция для этих двух случаев сильно различается, а точно учесть эти различия на фотопластинках было весьма проблематично – «в любом случае, остается ошибка не менее десятых долей секунды» [И1]. Сказанного с запасом достаточно, чтобы сделать логичный вывод: «В данном эксперименте измеряемая величина находилась глубоко под ошибками измерения… вывод о правильности ОТО, основанный на результатах этой экспедиции, является неправомерным и принципиально некорректным» [И1]. В условиях, когда инструментальные и методологические погрешности превышали искомый эффект, как минимум, в разы, Эддингтон пустился на хитрость: он отбраковал подавляющее большинство фотопластинок, расценив их как «неудачные». Методику этой отбраковки он не огласил – но едва ли можно сомневаться в том, что руководящим критерием было согласие с предсказаниями Эйнштейна: следовало учитывать только «правильные» смещения звёзд и не учитывать «неправильные». С помощью такой прогрессивной методики – т.е., через устранение из массива данных всего «лишнего» - можно «доказать» что угодно!

Вот почему, дорогой читатель, подробности эксперимента Эддингтона вы не найдёте в свободном доступе. Не странно ли это: скрывать от научной общественности детали того, как происходило «триумфальное подтверждение теории Эйнштейна»? Да нет: те, кто это скрывают – знают, что делают. Ибо не было там вообще никакого подтверждения – а не то что «триумфального».

Нам скажут, что были ведь другие экспедиции, повторившие результат Эддингтона! Вот именно – повторившие. Тропка была уже протоптана! Использовалось похожее оборудование и аналогичная методика обработки результатов – «они принципиально не обеспечивают суб-секундных точностей» [И1]. И это, напоминаем – без учёта хаотической рефракции света в солнечной короне! А ведь она, несомненно, имела место. «На фотографиях был получен набор хаотически смещенных во всех направлениях… "изображений звезд". Все это напоминало психиатрический тест - "пятна Роршаха", в которых, при желании, можно увидеть все что угодно» [И1].

Таким образом, ни Эддингтон, ни его последователи отнюдь не доказали, что свет испытывает, во-первых, действие тяготения, а, во-вторых, «гравитационную рефракцию» - обусловленную, якобы, зависимостью скорости света от гравитационного потенциала. Значит, эти эксперименты не бросают тень на логику «цифрового» мира, согласно которой, ни действия тяготения на свет, ни зависимости скорости света от гравитационного потенциала не существует в природе.

Уместно добавить, что ситуация совершенно аналогична и для случая радиоволн. Поэтому экспериментальные подтверждения действия тяготения на радиоволны и наличия гравитационного «притормаживания» радиоволн, проходящих вблизи массивного тела, получали по тем же принципам, как и в случае со светом – т.е. через заведомый обман. Так, для радиоимпульса, пролетающего рядом с Солнцем, гравитационное притормаживание дало бы увеличение времени его полёта, эквивалентное увеличению пути на 60 км! Шапиро утверждал, что именно это он и обнаружил при радиолокации Венеры, когда она была вблизи противостояния с Землёй. Об этом он заявил в статье с одиозным названием «Четвёртое подтверждение ОТО» [Ш4], но не привёл никаких экспериментальных данных – призывая верить ему на слово. С тех пор, в среде физиков, словосочетание «эффект Шапиро» имеет двойной смысл. Во-первых, это притормаживание радиоимпульсов при пролёте вблизи массивного тела. Во-вторых, это эффект, который «обнаружен» только на словах – без подтверждающих его экспериментальных фактов. Но этого позора оказалось мало. Спустя три года после своего «подтверждения ОТО», Шапиро предложил использовать радиоинтерферометры – пары радиотелескопов, разнесённых на межконтинентальные расстояния – для обнаружения гравитационного искривления траектории радиоимпульсов вблизи Солнца, принимая радиоимпульсы от квазаров [Ш5]. Надо иметь в виду, что, при работе радиоинтерферометра, информация о направлении на радиоисточник извлекается как раз из разности моментов прихода радиоимпульса на тот и другой радиотелескоп. А эта разность, в данном случае, сильно подвержена «эффекту Шапиро» - причём, в обоих его смыслах. Как же при этом удавалось подтверждать предсказания ОТО насчёт гравитационного искривления траектории радиоимпульса (см., например, [Л6])? На счастье экспериментаторов, опять же, имела место хаотическая рефракция радиоизлучения на неоднородностях плотности вещества в солнечной короне. Учесть эту рефракцию было невозможно, поэтому экспериментаторы помалкивали о ней в своих статьях. Зато статистика результирующих искривлений траекторий радиоимпульсов набиралась богатейшая – и из массива данных следовало отобрать лишь те случаи, которые «подтверждали ОТО». Всё тайное станет явным!

Опыт Басова (3.3) с полной очевидностью показывает, что световая энергия может быть переброшена на расстояние, практически, мгновенно – по крайней мере, для расстояний в несколько метров. Этот результат убийственен не только для теории относительности, но и для традиционных представлений о свете как о порциях энергии, летящих в пространстве между атомами со скоростью c. Выше (3.4) мы излагали, что кванты световой энергии отнюдь не летят в пространстве между атомами. Ведь, по логике «цифрового» мира, обладателем физических энергий в любых её формах может быть только вещество (1.1). Значит, и световая энергия может быть локализована только на веществе – на атомах. Отсюда и следует, что световая энергия должна передаваться с атома на атом без прохождения по разделяющему эти атомы пространству.

Такую «над-пространственную» передачу световой энергии на расстояние, непосредственно с атома на атом, могут обеспечить, на наш взгляд, лишь соответствующие программные средства, управляющие «цифровым» миром. Выше мы уже говорили о Навигаторе (3.4), который сканирует пространство со скоростью c в поисках атома-адресата, которому может быть переброшен квант световой энергии с возбуждённого атома – и, после того как атом-адресат найден, производится почти-мгновенный переброс этого кванта. Но, когда мы говорили об этих квантовых перебросах энергии возбуждения с атома на атом, у читателя могло сложиться впечатление, что энергия возбуждения прибавляется к энергии атома – так, что приобретение энергии возбуждения атомом увеличивает его полную энергию, а избавление от энергии возбуждения, наоборот, полную энергию уменьшает. Такие представления, на наш взгляд, некорректны, поскольку у атома, отдающего квант энергии возбуждения, и у атома, приобретающего такой же квант, полные энергии остаются прежними.

В самом деле, хорошо известно, что для ионизации атома, находящегося в возбуждённом состоянии, требуется сообщить ему меньшее количество энергии, чем для его ионизации из основного состояния. Причём, сумма энергии возбуждения и энергии связи атомарного электрона является при этом постоянной величиной, равной энергии ионизации из основного состояния. Напрашивается вывод о том, что энергия возбуждения не передаётся атому откуда-то извне – она появляется за счёт такой же по величине убыли энергии связи. Более подробно мы будем говорить об этом в 4.4; сейчас же обратим внимание на то, что у атома энергия возбуждения и энергия связи образуют сопряжённую пару энергий: увеличение одной из них происходит за счёт уменьшения другой, и наоборот – а их сумма остаётся постоянной. Применительно к распространению света это означает, что, при так называемом поглощении кванта света, атом не приобретает энергию сверх той, которую он имел: здесь происходит всего лишь превращение части энергии связи в энергию возбуждения – а полная энергия атома остаётся прежней. Аналогично, при так называемом излучении кванта, происходит противоположное перераспределение энергий в атоме – опять же, с оставлением его полной энергии прежней. Мы приходим к парадоксальному выводу: при квантовом перебросе энергии возбуждения с атома на атом, соответствующая порция энергии никуда не перемещается – полная энергия атома-отдающего не уменьшается, а полная энергия атома-принимающего не увеличивается. Другими словами, квантовый переброс энергии возбуждения представляет собой всего лишь скоррелированные перераспределения энергий у пары атомов: соответствующая управляющая программа скачком опускает вниз «разделительную планочку» между энергией возбуждения и энергией связи у атома-отдающего, и на столько же поднимает вверх эту «планочку» у атома-принимающего. Эти-то скоррелированные перераспределения энергий у пары атомов и порождают иллюзию перемещения кванта световой энергии с одного атома на другой. Как ни дико это выглядит на первый взгляд, но при распространении света никакого потока энергии в пространстве нет, ибо каждый атом остаётся при своём! Заметим, что такой подход легко и непринуждённо объясняет, почему при распространении света не переносится импульс (3.2)!

Ох, как трудно ортодоксам принять вывод об отсутствии потока энергии при распространении света! Больно сильно этот вывод задевает иллюзии, которые уютно утряслись в их подсознании. «Вы утверждаете, что по лазерному лучу не передаётся энергия? – радуются они. – Но это же смешно, молодой человек! Лазерный луч поджигает дерево, плавит и испаряет металл! Ясно же, что температура мишени повышается оттого, что туда вкачивается энергия, которая приходит по лазерному лучу!» Минуточку, любезные. То, что температура мишени повышается – это, действительно, ясно. Но температура мишени повышается вовсе не из-за того, что в неё вкачивается энергия. Вы, любезные, сначала разберитесь, что такое «температура» - это вовсе не мера энергосодержания. По всем канонам термодинамики и статистической физики, температура характеризует не энергосодержание ансамбля частиц, а статистику распределения энергий в этом ансамбле – т.е. как раз соотношения между энергиями из сопряжённых пар (5.9), в частности, энергий возбуждения и энергий связи у атомарных электронов. Лазерный луч всего лишь деформирует эти соотношения: энергии возбуждения в атомах мишени растут, а энергии связей в них уменьшаются, но суммы тех и других остаются прежними. Температура мишени при этом повышается, а полная энергия мишени – нет. При лазерном испарении и лазерной ионизации вещества всё происходит совершенно аналогично – но здесь в игру с превращениями энергий вступают кинетические энергии частиц, которые, вместе с собственными энергиями частиц, также образуют сопряжённые пары (5.9). Всё происходит в согласии с принципом автономных превращений энергии (4.4): увеличение температуры вещества обусловлено лишь перераспределениями энергий его частиц, но полные их энергии при этом не изменяются.

Таким образом, впечатляющим спецэффектам при лазерном воздействии на вещество ничуть не противоречит вывод о том, что при распространении света происходят перебросы, с атома на атом, не энергии, а всего лишь её перераспределений.

Приведём краткую сводку особенностей, ставящих под сомнение существование фотонов – как их традиционно представляют, т.е. как автономных порций световой энергии, летящих в пространстве со скоростью света.

Порции световой энергии существуют лишь на атомах: они перебрасываются на расстояние непосредственно с атома на атом, без прохождения по разделяющему их пространству – причём, практически, мгновенно (3.3). При этом не переносится импульс: никакой «отдачи» у атомов при квантовом перебросе световой энергии не происходит (3.2). Этот вывод совершенно естественен, если учесть, что при квантовом перебросе световой энергии производится не перенос энергии с атома на атом, а производятся всего лишь скоррелированные перераспределения энергий у этих атомов – так, что их полные энергии остаются прежними (3.10).

Фотоны, далее, не испытывают гравитационных сдвигов частоты (2.7): этим сдвигам подвержены лишь квантовые уровни энергии в веществе (4.7). Совершенно аналогично, фотоны не испытывают квадратично-допплеровских сдвигов частоты: этим сдвигам также подвержены лишь квантовые уровни энергии в веществе (4.7).

Фотоны не испытывают и линейно-допплеровских сдвигов частоты (1.8): с этими сдвигами имеет дело Навигатор (3.4), но сама перебрасываемая порция энергии не изменяется от того, что отдающий и принимающий атомы каким-то образом движутся.

Фотоны не могут превращаться в вещество, и обратно. Традиционные представления об аннигиляции и рождении электрон-позитронных пар, в которых подразумевается полноценность фотона как частицы, основаны на недоразумениях. Ниже (4.8) мы приведём анализ экспериментов, который показывает, что электрон и позитрон при аннигиляции не исчезают полностью: излучая, при таком событии, один гамма-квант с энергией 511 кэВ, они образуют структурное образование с массой электрона и нулевым электрическим зарядом – которое, при сообщении ему достаточной энергии возбуждения, способно диссоциировать на пару электрон-позитрон. К тому же, не наблюдалось прямого превращения гамма-кванта в электрон-позитронную пару: эта пара вылетает из ядра, в которое попадает гамма-квант с достаточной энергией (4.8). Таким образом, о взаимопревращениях между веществом и фотонами говорить не приходится.

Фотон, конечно, не обладает никаким спином. Спин – это придумка теоретиков даже для случая электрона (4.2), а для случая фотона – это, если можно так выразиться, придумка в квадрате. Не существует ни физической модели спина фотона, ни экспериментальных подтверждений его наличия. Какие тут могут быть подтверждения? «Подтверди то – не знаю, что» - не иначе. Впрочем, из высоконаучных соображений следует, что частицы с целым спином – который приписан и фотону – обязаны подчиняться вполне определённой квантовой статистике, по типу Бозе-Эйнштейна. А именно: в коллективе таких частиц, все они стремятся пребывать в одинаковых состояниях – в частности, иметь одинаковую энергию. И нас пытаются убедить в том, что фотоны именно так себя и ведут. И даже пример приводят: лазерную генерацию! Тогда позвольте заметить, что лазерное излучение составляет ничтожнейший процент от всего излучения в природе: оно является не правилом, а жалким исключением. Хуже того, даже в случае лазера следует очень постараться, чтобы подавить все моды, кроме одной, чтобы обеспечить одночастотный режим генерации – ведь любая другая мода «пролазит» при малейшей возможности! Где же оно, стремление фотонов иметь одинаковую энергию?! Да и вообще, говорить о статистике фотонов просто смешно. Сделай одни условия генерации – «статистика» фотонов будет одна, а сделай другие – и «статистика» будет другая. Детский сад какой-то!

И, в довершение ко всему этому, на фотоны не действует тяготение (3.9)!

Что же остаётся от традиционной концепции фотона? Эта концепция совершенно излишняя с позиций нашей модели «цифрового» физического мира, процессы в котором происходят в результате работы программных предписаний, обеспечивающих выполнение физических законов. Так, распространение света управляется Навигатором (3.4). Такой подход избавляет от необходимости приписывать фотону необъяснимые свойства, прикрываемые термином «корпускулярно-волновой дуализм», поскольку за особенности распространения света, в том числе и за волновые свойства, отвечает Навигатор. При таком подходе немедленно устраняются парадоксы, связанные с «редукцией волнового пакета» для фотона в явлениях интерференции и дифракции, с «интерференцией» фотонов, летящих поодиночке, с «интерференцией» фотона с самим собой, и т.п.

Физика радикально упрощается, если осознать, что никаких фотонов нет!

А1. С.Артёха. Критика основ теории относительности. Веб-ресурс http://www.antidogma.ru/russian/

А2. Н.Е.Алексеевский и др. ЖЭТФ, 43, 3 (1962) 790.

А3. И.А.Авенариус и др. Письма в ЖЭТФ, 14, 9 (1971) 484.

А4. A.M.Akulshin, S.Barreiro, A.Lezomo. Phys.Rev.Lett., 83 (1999) 4277.

Б1. М.Борн. Атомная физика. «Мир», М., 1965.

Б2. Н.Г.Басов, Р.В.Амбарцумян, В.С.Зуев, и др. ЖЭТФ, 50, 1 (1966) 23.

В1. L.J.Wang, A.Kuzmich, A.Dogaru. Nature, 406 (2000) 277.

Г1. А.А.Гришаев. К вопросу о равновесном излучении. – Доступна на http://newfiz.narod.ru

Г2. М.М.Гуревич. УФН, 56, 3 (1955) 417.

Г3. М.М.Гуревич. УФН, 78, 3 (1962) 463.

Г4. А.А.Гришаев. О так называемом давлении света. – Доступна на http://newfiz.narod.ru

Г5. А.А.Гришаев. Рассеяние рентгеновских лучей: о чём свидетельствует анти-комптоновская компонента. – Там же.

Г6. А.А.Гришаев. Новый взгляд на сущность эффекта Мёссбауэра. – Там же.

Г7. В.И.Гольданский и др. ЖЭТФ, 54, 1 (1968) 78.

Г8. А.А.Гришаев. О главной причине эволюций орбиты ИСЗ «Эхо-1». – Доступна на http://newfiz.narod.ru

Г9. А.А.Гришаев. Навигатор квантовых перебросов энергии. – Там же.

Г10. А.А.Гришаев. Проблема «волны-кванты» в абсолютных измерениях лазерных частот. – Там же.

Г11. А.А.Гришаев. Классификация различных методик измерения скорости света в вакууме. Измерительная техника, 2 (1996) 3. – Доступна также на http://newfiz.narod.ru

Г12. А.А.Гришаев. О причинах сдвигов спектральных линий звёзд. – Там же.

Д1. В.Демтрёдер. Лазерная спектроскопия. Основные принципы и техника эксперимента. «Наука», М., 1985.

Д2. Ю.С.Домнин, Г.А.Ёлкин, А.В.Новосёлов, и др. Применение холодных атомов цезия в квантовых стандартах частоты. Квантовая электроника, 34, 12 (2004) 1084.

Д3. Document conserning the New Definition of the Metre. Metrologia, 19 (1984) 163.

Е1. А.С.Енохович. Справочник по физике и технике. «Просвещение», М., 1976.

И1. Г.Ивченков. Самое важное подтверждение ОТО, или что измерил лорд Эддингтон в 1919 г. http://new-idea.kulichki.net/?mode=art&pf=eddington.htm

К1. A.H.Compton. A quantum theory of the scattering of X-rays by light elements. Phys.Rev., 21, 5 (1923) 483.

К2. Crane, Gaerttner, Turin. Phys.Rev., 50 (1936) 302.

К3. Р.Н.Кузьмин и др. ЖЭТФ, 56, 1 (1969) 167.

К4. Космонавтика. Энциклопедия. В.П.Глушко, гл. ред. «Сов. энциклопедия», М., 1985.

К5. А.А.Курский. Почему постоянна «солнечная постоянная». Веб-ресурс http://kaa.inauka.ru Статья «Электромагнитное взаимодействие», Прил.1.

Л1. Ж.Леконт. Инфракрасное излучение. «Гос. изд-во физико-математической литературы», М., 1958.

Л2. П.Н.Лебедев. Физические причины, обусловливающие отступления от гравитационного закона Ньютона. В: «Избранные сочинения», А.К.Тимирязев, ред. «Гос. изд-во технико-теоретической литературы», М.-Л., 1949. Стр.181-188.

Л3. П.Н.Лебедев. Опытное исследование светового давления. Там же, стр.151-180.

Л4. В.И.Левантовский. Механика космического полёта в элементарном изложении. «Наука», М., 1974.

Л5. Г.С.Ландсберг. Оптика. «Гос. изд-во технико-теоретической литературы», М.-Л., 1940.

Л6. D.E.Lebach, B.E.Corey, I.I.Shapiro, et al. Phys.Rev.Lett., 75, 8 (1995) 1439.

М1. D.O.Muhleman, R.H.Hudson, D.B.Holdridge, et al. Science, 132 (1960) 1487.

Н1. D.E.Nagle et al. Phys.Rev.Lett., 5, 8 (1960) 364. Имеется перевод: Эффект Мессбауэра. Сборник статей. Ю.Каган, ред. «Изд-во иностр. литературы», М., 1962. Стр. 323, статья 30.

О1. А.Н.Ораевский. Успехи физических наук, 168, 12 (1998) 1311.

П1. М.Планк. К теории распределения энергии излучения. Избранные труды, «Наука», М., 1975.

П2. М.Планк. О законе распределения энергии в нормальном спектре. Там же.

С1. Р.А.Сапожников. УФН, 70, 2 (1960) 387.

С2. О.Струве, Б.Линдс, Э.Пилланс. Элементарная астрономия. «Наука», М., 1967.

С3. О.Струве, В.Зебергс. Астрономия XX века. «Мир», М., 1968.

С4. A.M.Steinberg, P.G.Kwait, R.Y.Chiao. Phys.Rev.Lett., 71 (1993) 708.

С5. Солнце. В: Курс астрофизики и звёздной астрономии. А.А.Михайлов, ред. Т.3, часть 1. «Наука», М., 1964.

С6. Дж.Дж.Странатан. «Частицы» в современной физике. «Гос. изд-во технико-теоретической литературы», М.-Л., 1949.

Т1. П.С.Тартаковский. Кванты света. «Госиздат», М.-Л., 1928.

Ф1. Физический энциклопедический словарь. А.М.Прохоров, гл. ред. «Советская энциклопедия», М., 1983.

Ф2. К.Фрум, Л.Эссен. Скорость света и радиоволн. «Мир», М., 1973.

Х1. R.Hofstadter, J.A.McIntyre. Phys.Rev., 78, 1 (1950) 24.

Ч1. S.Chu, S.Wong. Phys.Rev.Lett., 48, 11 (1982) 738.

Ш1. Э.В.Шпольский. Атомная физика. Т.1. «Наука», М., 1974.

Ш2. I.I.Shapiro, H.M.Jones. Science, 132 (1960) 1484.

Ш3. R.S.Shankland. Phys.Rev., 52 (1937) 414.

Ш4. I.Shapiro. Fourth test of general relativity. Phys.Rev.Lett., 13 (1964) 789.

Ш5. I.I.Shapiro. Science, 157 (1967) 806.

Э1. А.Эйнштейн. Физика и реальность. Сборник статей. «Наука», М., 1965.