Ответы

Давайте начнем с варианта (а). Если вы поднесете к зеркалу газету, то шрифт в отражении будет расположен справа налево и его будет трудно прочитать. Представьте, что текст напечатан на прозрачном пластике, тогда если вы прижмете текст к зеркалу, то увидите, что отражение точно совпадает с оригиналом. Зеркало не «переворачивает» отражение.

Это станет еще более очевидным, если вы поднесете к зеркалу стрелку-указатель. Расположите ее горизонтально так, чтобы она показывала налево — отражение стрелки в зеркале будет указывать в том же направлении. Как видите, ничего не «перевернулось». Теперь поверните стрелку, чтобы она показывала направо — то же произойдет и с отражением.

Это справедливые рассуждения, и все же мы знаем, что какой-то «переворот» происходит, хотя, как мы только что увидели, это не совсем то, что подразумевают обычно люди, рассуждая на эту тему. Ваш интервьюер поэтому обычно скажет: «Да, но если отражение не „перевернутое“, почему вы не можете читать отраженный в зеркале газетный текст? Почему, если текст напечатан на прозрачной пленке, вам нужно повернуть его справа налево, а не перевернуть вверх ногами, чтобы отраженный текст можно было прочитать?»

Ответ (б) предполагает обратное: в зеркале изображение переворачивается в любом направлении. Если зеркало на полу — то есть «смотрит вверх» — вы можете сказать, что оно меняет местами верх и низ. Зеркало, ориентированное на северо-восток, меняет местами север и юг или северо-восток и юго-запад. Зеркало, повернутое налево, — правое и левое. Нет никакого «предпочитаемого» направления. Никакие физические свойства зеркал не предписывают им менять местами именно правое и левое.

Интервьюера, вероятно, заинтересует, почему распространилось именно такое заблуждение, будто зеркала меняют местами правое и левое направления. Вы можете ответить, что это связано с культурой, традициями и привычными стандартами архитектуры и дизайна интерьеров: зеркала обычно располагают именно на стенах прямоугольных комнат и залов, а не на углах или потолках. Именно поэтому зеркала «переворачивают» изображения именно в горизонтальном направлении (юг и север, запад и восток), а не в вертикальном (верх и низ). Такая горизонтальная трансформация направлений в отражении традиционно описывается как замена «правового» на «левое». Это проще и понятнее для людей, чем использование географических терминов, таких как «север» и «восток», поскольку географические направления «север» и «юг» не зависят от расположения зеркала, они абсолютны, а не относительны как «правый» и «левый», а мы понимаем, что зеркальное отражение — это относительное явление.

Объяснение (б) обладает рядом достоинств, но все же не отвечает на основной вопрос. Где бы вы ни были: в номере отеля в Лас-Вегасе, где зеркало расположено на потолке, в эскимосском иглу, юрте кочевников, зеркальном зале во время карнавала и вообще в самых непривычных для западного человека помещениях или интерьерах, которые только можно выдумать, — вы все равно не сможете прочитать отражение газетного текста в зеркале, потому что оно «перевернуто справа налево». Почему?

Давайте поставим вопрос прямо: почему изображение переворачивается в зеркале? На этот раз давайте будем тщательно подбирать термины и формулировки и дадим обобщенное определение того, что это значит — зеркало «переворачивает изображение».

Объяснение (а) верно в том смысле, что зеркала не обязательно меняют местами именно правое и левое. Было бы странно, если бы так происходило: ведь «правое» и «левое» определяется по отношению к наблюдателю. Каким образом глупый кусок стекла может «догадаться» о том, что кто-то на него смотрит, да еще и определить, как ориентирован наблюдатель? Но для того чтобы последовательно менять местами именно правое и левое, это нужно знать.

Гораздо более вероятно (и верно), что направление, в котором изменяется ориентация отражения в зеркале, зависит от положения в пространстве самого зеркала. Именно это суть объяснения (б). Меняя ориентацию зеркала в пространстве, вы можете его заставить «переворачивать» изображения в любом направлении.

Но как именно это происходит? Эксперимент со стрелкой показал, что, если стрелка расположена параллельно поверхности зеркала, ее отражение не «переворачивается» и указывает в том же направлении, что и сама стрелка. Можно ли расположить стрелку так, что ее отражение будет указывать в другом направлении, чем сама стрелка? Да. Так произойдет, если стрелка будет нацелена прямо на зеркало (направление «от вас»). Тогда ее отражение будет указывать на вас, а не в глубину зеркала. Или наоборот: сделайте так, чтобы стрелка указывала на вас (от зеркала). Отражение стрелки будет указывать не на вас, а в глубину зеркала.

Несколько многословное, но точное определение того, что происходит с отражением в зеркале, будет таким: в зеркале меняется направление «к зеркалу» (или «в зеркало») на «от (или „из“) зеркала» и наоборот. Когда вы смотрите в зеркало, то те предметы, которые в нем оказываются расположенными перед вами, на самом деле находятся позади вас. В то же время направления, параллельные поверхности зеркала, такие как правое и левое, верх и низ, не «переворачиваются», не меняются местами в отражении.

Это настолько очевидное явление, что мы обычно не обращаем на него внимания. В большинстве случаев вы не воспринимаете зеркальное отражение как «зазеркальный мир». Вы знаете, что видите в зеркале ваше собственное лицо, находясь в вашей собственной комнате. Наш мозг учитывает перемену направления в зеркало/из зеркала и интерпретирует перевернутое в зеркале изображение как реальный мир.

Эта полезная иллюзия подводит нас только тогда, когда мы имеем дело с некоторыми асимметричными объектами и действиями. Резьба на винтах, раковины улиток, узлы, ножницы существуют в двух зеркально симметричных формах. Самый знакомый для нас из подобных объектов — это наши собственные руки. Левая рука похожа на правую во всех деталях и в то же время не похожа.

Ваши правая и левая рука — «зеркальные отражения» друг друга. Соедините кончики пальцев правой руки с кончиками пальцев левой — впечатление будет таким, будто ваши руки разделяет поверхность зеркала. Кажется, что левая рука — это отражение в зеркале правой, и наоборот.

Вот где возникает путаница. В английском языке, как и во многих других языках, принято называть две зеркально симметричных формы одного и того же явления «правой» и «левой». Это просто риторическое выражение. Оно не имеет ничего общего с правым и левым направлением. Мы с таким же успехом могли бы назвать правую и левую резьбу резьбой «А» и резьбой «Б», или «плюс» и «минус», или «нормальной» и «обратной».

Одно из свойств зеркальной симметрии заключается в том, что любой из асимметричных объектов, отраженный в зеркале, трансформируется в свой зеркально симметричный аналог. Очевидно, что нашему мозгу трудно корректно воспринимать зеркальные аналоги привычных асимметричных объектов. Поскольку большинство печатных текстов абсолютно асимметричны, их зеркальные отражения выглядят странно, и мы не можем их прочитать. Асимметричные действия, такие как стрижка ножницами, могут стать чрезвычайно трудными, если вы смотрите на свое зеркальное отражение.

Нам достаточно трудно описать подобные затруднения словами. Если постараться найти наиболее точную формулировку, можно сказать, что в зеркальном отражении левоасимметричные объекты становятся правоасимметричными. В обыденной речи эта формулировка упрощается, и говорят, что в зеркале «правое» становится «левым» — хотя это уже иное и по существу неверное заключение. Мы часто соглашаемся с различными утверждениями и повторяем их, не особенно задумываясь о сути того, что мы слышим. Это как раз такой случай.

Вот краткое резюме приведенного выше анализа. Зеркало не делает правое левым, а верх низом. Оно «перевертывает» только два направления: к зеркалу и от зеркала. Это изменяет так называемые «правые» и «левые» формы асимметричных объектов, так что «правосимметричная» форма становится «левосимметричной», и в итоге отражение текста в зеркале становится нечитаемым.

Для ответа на этот вопрос требуется изменение парадигмы анализа. Вас спрашивают о том, почему в зеркале правое становится левым, хотя на самом деле этого не происходит. Многие кандидаты во время интервью так и не могут выпутаться из этой ловушки. Этот вопрос тестирует готовность кандидата оспаривать общепринятые утверждения, даже если их высказывает «начальник».

Мартин Гарднер упоминал этот вопрос в 1950-х годах, и, по-видимому, именно он сформулировал его как логическую задачу. Он написал целую книгу The ambidextrous Universe («Вселенная-амбидекстр[*]»), в которой анализируется проблема зеркальной симметрии и асимметрии, а также ее разнообразные и многочисленные следствия.[132]

В какую сторону должен поворачиваться ключ в замке дверцы автомобиля, когда автомобиль отпирают?

Загадки дзэн-буддистов обычно строились на абсурдных дилеммах, чтобы подчеркнуть, что в мире нет жестких противоположностей и границ. Можно ли сказать, что Будда и собака тождественны по свой природе? Можно ли назвать короткий посох коротким или нельзя? Загадка Microsoft об автомобильном замке относится к тому же типу.

Некоторые кандидаты, проходящие интервью, думают, что неважно, что выбрать — правое или левое. Настоящая цель вопроса — проверить, можете ли вы сделать выбор между альтернативами А и В, которые на первый взгляд ничем не отличаются друг от друга, и не «застрять» на стадии принятия решений. (В компьютерном бизнесе также приходится принимать подобные решения. Если вас примут на работу, вам придется участвовать в совещаниях и объяснять и отстаивать там собственные решения, не всегда бесспорные и обоснованные.)

На самом деле на данный вопрос есть более обоснованный и более удачный ответ. И вот почему: вам нужно вытянуть вперед правую руку, как будто вы держите в ней ключ (если вы левша, притворитесь на время правшой). Вам нужно сжать руку в кулак ладонью вниз так, как вы делаете, зажимая ключ между большим пальцем и средним суставом указательного пальца.

Теперь поворачивайте кисть руки по часовой стрелке настолько, насколько сможете. Скорее всего вы без труда повернете кисть на 180 градусов, теперь ладонь уже смотрит вверх, а не вниз.

Попробуйте сделать то же самое, но поворачивайте кисть против часовой стрелки. Окажется, что даже на 90 градусов кисть повернуть трудно: для большинства людей поворот на 90 градусов в этом направлении — предел.

Анатомия нашей руки, запястья и кисти такова, что для правшей поворачивать ключ по часовой стрелке (так, что бородка ключа поворачивается направо) легче. Вот она — асимметрия. Естественно, у левшей все наоборот. Но левшей среди людей гораздо меньше, чем правшей, именно поэтому и можно утверждать, что существует предпочтительное направление поворота ключа.

Похоже, мы нашли обоснование ответа. Но так ли это? Ведь, если говорить о длительных промежутках времени, мы запираем машину ровно столько же раз, сколько отпираем ее. Одно из этих двух движений более «легкое», а другое — «трудное». Но ведь шесть раз — это ровно столько же, сколько полдюжины. Похоже, говорить об асимметрии нет смысла.

Однако интервьюеры Microsoft, насколько мне известно, всегда спрашивают только об отпирании двери и никогда о запирании. Учитывая, что для большинства людей поворачивать ключ в замке по часовой стрелке легче, можно привести несколько доводов в пользу того, что более легкое и «естественное» движение стоит использовать именно при отпирании двери:

— если вы отпираете незнакомую машину, то, вероятно, попробуете сначала более естественное движение. Для большинства людей это поворот по часовой стрелке. Более удобно конструировать замок так, чтобы именно то направление поворота ключа, которое, вероятно, предпочтет большинство людей, оказалось верным;

— водители, оставляя машины на парковке, обычно запирают их. Перед поездкой нужно снова отпереть дверцу, если это сделать легко, то машина будет представляться владельцу «более дружелюбной», удобной для пользователя. Разработчики программного обеспечения знают, как важно, чтобы программа загружалась как можно быстрее, если же этого не происходит, то люди менее склонны использовать данную программу или данный элемент программы;

— после широкого распространения электронных автомобильных замков с дистанционным пультом управления ключи используются теперь в основном только если села батарейка или вышла из строя электроника. Поскольку ключи используются редко, скорее всего большинство людей не помнит, в какую сторону нужно поворачивать ключ. В таком случае приводившиеся выше доводы верны: нужно сделать так, чтобы замок открылся после того, как владелец машины испробует первое же наиболее естественное направление поворота ключа. Вы чаще всего обнаружите, что батарейка села, именно когда попытаетесь открыть запертую машину. В этой ситуации опять-таки более выгодно, чтобы машину было легко открыть, особенно если есть проблемы;

— бывают такие ситуации, когда быстро открыть машину — это вопрос жизни и смерти. Допустим, если вы попали в снежный буран в Каскадных горах, то возможность быстро укрыться в машине может спасти вам жизнь. Если за вами гоняется по пятам маньяк с топором, вам также нужно будет как можно быстрее оказаться в вашей машине, чтобы спастись от него. Иногда замки заедает, а некоторые люди страдают артритом или получают травму, и им трудно повернуть ключ в замке. Можно представить себе такую ситуацию, когда жизнь человека зависит от того, сумеет ли он открыть дверцу автомобиля, и сил уже почти не осталось — вот когда вам наверняка захочется, чтобы замок отрывался в «легкую сторону». Сравните это с ситуацией, когда нужно запереть дверцу машины снаружи (только в этом случае вам понадобится ключ) — здесь речь идет не о спасении жизни, а просто о защите собственности.

Ни одна из приведенных причин не является абсолютно неоспоримой — речь идет или о маловероятных ситуациях, или о не слишком важных удобствах. Подобно вопросу о том, с какой стороны располагать сливное отверстие в круглой ванне, — некоторые проблемы дизайна решаются на основе «микроаргументов» в пользу того или иного решения.

В реальности замок дверцы большинства автомобилей отпирается поворотом ключа по часовой стрелке со стороны водителя, а вот со стороны пассажира дверца обычно открывается при помощи поворота ключа против часовой стрелки. Другими словами, вы открываете дверцу, поворачивая ключ в сторону ближайшего к замку края дверцы. Это обычная практика и для замков, запирающих двери квартир. Большинство людей подсознательно усваивают это правило, даже если не подозревают о нем. Это еще один довод в пользу того, что водитель, который впервые пробует открыть дверцу незнакомого автомобиля, скорее всего попробует повернуть ключ по часовой стрелке.[133]

Короче говоря, и традиции, и эргономика подсказывают, что ключ должен отпирать замок дверцы со стороны водителя, поворачиваясь по часовой стрелке (направо). Люди из Microsoft просто помешаны на эргономике и еще больше любят, чтобы все следовали одинаковым стандартам.

Почему так происходит: когда вы включаете горячую воду в отеле, горячая вода из крана течет сразу же?..

Дело в том, что в домах большинства людей бойлер, нагревающий воду, отделяет от крана, из которого вытекает горячая вода, не один десяток метров труб. Трубы для горячей воды, конечно, никто не нагревает. Если кран для горячей воды в вашем доме какое-то время не открывается, вода в трубах остывает до температуры окружающей среды, поэтому, когда вы включаете горячую воду, сначала должна протечь остывшая в трубах вода, и только затем пойдет вода горячая.

Можно придумать несколько способов, чтобы из крана мгновенно текла горячая вода. Вы можете установить специальный нагреватель для каждого крана горячей воды как можно ближе к нему. Можно также установить систему подогрева труб. Это приемлемые (хотя и неверные) ответы во время интервью.

Вот как решается проблема в реальности: в отелях и некоторых жилых домах установлена система циркуляции горячей воды. Это насос, подсоединенный к специальной дополнительной трубе, по которой вода течет «назад» к бойлеру. «Обратная» труба проходит от самого дальнего от бойлера крана мимо всех остальных к бойлеру. Насос медленно прокачивает горячую воду через систему, чтобы она никогда не остывала. Именно поэтому, когда вы включаете кран, из трубы сразу течет горячая вода.

Основное преимущество этой системы по сравнению с приведенными выше предложениями заключается в том, что ее легко и дешево эксплуатировать. «Обратная» труба может быть достаточно тонкой — обычно это гибкая пластмассовая трубка, которую очень легко подсоединить.

Как делают конфеты M&M's?

Основной вопрос: как удается изготавливать абсолютно гладкие многослойные конфеты дисковидной формы в огромных количествах на полностью автоматизированных линиях — человеческая рука впервые прикасается к этим конфетам только после того, как открывается пакет. Просто обмакнуть шоколад в расплавленную сахарную глазурь — это плохое решение. Вам ведь придется куда-то поместить конфеты, пока глазурь будет затвердевать. Если сделать так, одна сторона конфеты окажется плоской, как у обычных шоколадных конфет. Один из изобретательных (но неверных ответов) был таким: «У них есть противень с горячим кипящим шоколадом, арахис специально замораживают и „простреливают“ через горячий шоколад, который мгновенно затвердевает на конфете еще до того, как она коснется конвейера».[134]

Реальный метод, используемый компанией Mars, и прост, и остроумен. К несчастью, догадаться, как он работает, очень трудно, если только вы не эксперт по технологиям изготовления конфет. Шоколадные сердцевины «обычных» конфет M&M's сначала отливаются в небольших формах. Затем эти шоколадные эллипсоиды помещают в большой вращающийся барабан, похожий на бетономешалку. Пока конфеты «трясутся» в этом барабане, на них напыляют сахарную глазурь, которая затвердевает и становится белой твердой оболочкой конфеты. Поскольку конфеты постоянно двигаются и перемешиваются, они не слипаются в комок. Кроме того, благодаря постоянному движению и соударениям конфеты становятся гладкими и все неровности удаляются. Тот же принцип вращающегося барабана используется для шлифовки драгоценных камней.

Потом конфеты еще раз опрыскивают, но уже цветной сахарной глазурью, которая застывает поверх белой глазури.

Еще одна тайна: как им удается печатать маленькие буквы «m» на-конфетах — очевидно, это делается не вручную. Причем эти буквы всегда находятся в середине одной из двух плоских сторон конфеты. Это значит, что каждая из конфеток должна быть проштампована клише с красителем. Вот в чем секрет: конфетки попадают на конвейер, на котором тысячи углублений по форме конфеток M&M's. Каждая конфетка попадает в одно из этих углублений. Затем к каждой из них очень легко и осторожно прикасается резиновый штамп с белым съедобным красителем — и на конфетах появляются знакомые буквы «m».

Это одна из нескольких головоломок Microsoft, время и место появления которой я смог установить. Джон Сполски, работавший в команде, разрабатывавшей электронные таблицы Excel, придумал ее примерно в 1990 году. «Все, что я помню, — мы болтали с другими менеджерами программ в Microsoft и спрашивали друг друга: «А какие вопросы ты используешь?». Я сказал: "Вы знаете, а я вот подумал про M&M's. Я буду спрашивать про M&M's". Мне сказали: «Вряд ли это будет хорошим вопросом. Очень трудно догадаться. Нужно много знать про шоколад»».

Сполски рассказывал, что он использовал этот вопрос всего несколько раз. Сейчас он считает, что есть более удачные вопросы. Так же, как и вопрос о форме крышки люка, вопрос о M&M's получил широкую известность и используется другими фирмами.

Интервьеры не шутят, когда говорят, что тому, кто задает вопрос, не обязательно знать «правильный ответ». Сполски признал, что даже он сам не знает, как делаются M&M's. Это не обязательно знать, чтобы оценивать ответы кандидатов на работу. Цель этого вопроса, как и большинства других, — проверить, может ли кандидат сказать по этому поводу что-то убедительное и, напротив, не давать глупых ответов.

Вы плывете в лодке и выбрасываете за борт чемодан — поднимется или опустится уровень воды?

Это простой вопрос, если вы знаете, что плавающие в воде предметы вытесняют равное им по весу количеству воды. В этом весь трюк. Наверное, большинство кандидатов на работу в корпорации Microsoft, получивших техническое образование, когда-то слышали об этом, хотя многие из них не вполне уверены, о чем именно шла речь (гммм… Что же это было — вес или объем воды, которые вытесняет предмет?). В конце концов для создания компьютерных программ это помнить необязательно.

Вот способ решения этой задачи, для использования которого практически не нужны математические и физические знания. Давайте начнем с самых основ. Каждый раз, когда вы выбрасываете что-то из лодки, она становится легче и поэтому всплывает. Правильно?

К несчастью, вопрос не об этом. Вас спрашивают, повысится или понизится уровень воды, а не всплывает ли лодка.

Обычно, если вы плаваете в достаточно большом водоеме, вы не обращаете внимания на уровень воды, если он достаточен, чтобы лодка не села на мель. Когда вы выбрасываете из лодки чемодан, то заметного на глаз изменения уровня воды не произойдет. Вопрос в том, изменится ли в принципе уровень воды и как.

Единственный фактор, который может изменить уровень воды, это объем погруженных в нее объектов. Замысловатый термин, который придумали для этого ученые, — «водоизмещение». Представьте себе игрушечный кораблик, плавающий в ванне. Погруженный в воду корпус кораблика занимает определенный объем, который соответственно не может занимать вода. Этот объем и называется водоизмещением кораблика. Это не полный объем кораблика, а только та его часть, которая находится ниже ватерлинии.

Уровень воды в ванне зависит от суммы водоизмещении всех игрушечных корабликов, резиновых уточек и других объектов, которые плавают в ванне или «утонули» в ней. Добавьте еще несколько корабликов, и количество вытесненной воды увеличится. Вытесненная вода должна где-то находиться, поэтому уровень воды повысится. Если вы, наоборот, вынете из воды несколько корабликов, количество вытесненной воды уменьшится, и уровень воды понизится.

Все это относится и к озерам, и к морям. Дело только в том, что у естественных водоемов сложный рельеф дна, поэтому труднее представить изменения уровня воды визуально, но если речь идет об океане, очевидно, что изменения в любом случае микроскопические.

Следовательно, вопрос можно переформулировать таким образом: «Если выбросить из лодки чемодан, изменится ли количество вытесненной воды?» Мы знаем, что лодка после этого станет легче. Это уменьшит ее осадку в воде, и, следовательно, уменьшится количество воды, вытесненное лодкой, но когда чемодан плюхнется в воду, он также вытеснит какое-то количество воды. Каким же будет суммарный эффект: позитивным, негативным или нулевым?

Для ответа на этой вопрос мы должны установить соотношение между весом и объемом вытесненной воды. Вот «умственный физический эксперимент», решающий эту задачу.

Представьте себе надувной мяч (вроде тех, которыми играют на пляже), который плавает в ванне. Такой мяч обычно очень легкий — его оболочка сделана из тонкого пластика, а внутри — воздух, поэтому он будет плавать на поверхности воды, практически не погружаясь в нее и не вытесняя воды — правильно? Вывод: если вес объекта очень мал, он практически не вытесняет воду и не изменяет уровень воды.

Теперь представьте, что у вас есть такой же пляжный мяч, но вам каким-то образом удалось засунуть внутрь этого мяча двухкилограммовый кирпич. Этот дополнительный вес приведет к тому, что мяч глубже погрузится в воду и вытеснит больше воды. Два килограмма дополнительного веса увеличат (мы не знаем точно насколько) количество вытесненной воды.

Теперь представьте себе третий пляжный мяч, внутри которого ровно два килограмма воды. У него тоже будет более низкая осадка по сравнению с первым мячом. Ваша «умственная физическая модель», надеюсь, достаточно точна, чтобы подсказать, что мяч будет погружаться в воду до тех пор, пока уровень воды внутри мяча не будет почти таким же, как снаружи. (Если бы мяч был сделан из сверхпрочного и сверхтонкого пластика, изготовленного при помощи нанотехнологий, внутренний и внешний уровни воды оказались бы абсолютно одинаковыми. Мяч был бы просто пузырем на поверхности воды, как пузыри на воде во время дождя.)

Это значит, что два килограмма воды вытесняют ровно два килограмма воды. И вода в этом отношении ничем не отличается от других веществ и материалов. Мы могли бы поместить внутрь мяча четыре килограмма и 500 граммов воды или любое другое количество воды, которое может поместиться внутри мяча, — принципиально ничего не меняется. Мяч вытеснит ровно столько воды, чтобы внутренний и внешний уровень воды уравнялись.

При этом даже совершенно не важно, какова форма мяча. Это может быть и детский плавательный круг, на котором сверху голова лошадки, — налейте внутрь этого круга два килограмма воды, и он также погрузится ровно настолько, чтобы вытеснить два килограмма воды. Или пластиковая игрушка в форме лодки или чемодана — ничего не изменится. Единственный параметр, который играет роль, — вес воды, налитой внутрь этого предмета.

Давайте вернемся к пляжным мячам: у нас есть мяч, внутри которого два килограмма воды, и мяч, внутри которого двухкилограммовый кирпич. Повлияет ли как-то «начинка» мячей на количество вытесненной воды? Вы, наверное, согласитесь, что нет. Если вы простите мне антропоморфизм — «леди Гравитация» слепа. Она не видит, что внутри одного мяча кирпич, а внутри другого — вода. Она просто ощущает два килограмма груза внутри объекта какой-то формы. Только этот вес определяет физические характеристики плавающих объектов.

Вывод: для плавающих в воде объектов вытеснение воды зависит только от их веса — и точка. Если вам все-таки не совсем понятно, о чем идет речь, проделайте еще один умственный эксперимент. Допустим, у вас есть надувная игрушка для пляжа той же формы, что и лодка, внутри которой два килограмма воды. Теперь перелейте один килограмм воды в другую плавающую в бассейне игрушку, форма которой — точная копия чемодана фирмы Samsonite. Вес вытесненной воды до этой операции был два килограмма, а после, поскольку 1 + 1 = 2, также остался неизменным.

Итак, то, что чемодан оказался за бортом, не меняет общий вес вытесненной воды (или уровень воды), если предположить, что чемодан будет плавать в воде.

Последняя деталь очень важна. Как известно каждому носильщику на вокзале, чемодан одного и того же размера может оказаться и очень легким, и очень тяжелым. Обычный чемодан, внутри которого сложена одежда и есть много воздуха, скорее всего будет плавать на поверхностности, а вот чемодан, заполненный свинцовыми грузилами или хрустальной посудой, немедленно утонет.

Представим, что мы выбросили за борт такой тяжелый чемодан, предварительно привязав его прочной леской к лодке. Сначала, лодка всплывет, но, когда чемодан погрузится на глубину, определяемую длиной лески, и леска натянется, лодка снова погрузится, потому что ее потянет вниз груз подвешенного к ней тяжелого чемодана. Суммарное водоизмещение (вес вытесненной воды) лодки и чемодана останется неизменным. Общий вес системы лодка — чемодан не изменился, следовательно, и вес вытесненной воды не изменится до тех пор, пока и лодка, и чемодан как единое целое плавают в воде. А вот если вы перережете леску, чемодан утонет и окажется на дне, а лодка немного всплывет. Очевидно, что общее количество вытесненной воды при этом уменьшится, а уровень воды в водоеме понизится.

Ответ на задачу таков: выброшенный чемодан никак не изменит уровень воды, если он будет плавать в воде. Если же он утонет — уровень воды понизится.

Сколько всего настройщиков пианино в мире?

В 1940-х и 1950-х годах нобелевский лауреат физик Энрико Ферми любил озадачивать подобными абсурдными вопросами, предложением оценить какие-то количественные параметры, не пользуясь статистическими данными, своих студентов в Чикагском университете. Хотя «вопросы Ферми» до сих пор используют некоторые преподаватели физики, они теперь гораздо больше известны как один из приемов, используемых интервьюерами при оценке кандидата на работу. Возможно, самый известный из «вопросов Ферми» (вероятно потому, что он самый глупый) — это предложение оценить количество настройщиков пианино в Чикаго.

Версия этого вопроса, используемая Microsoft, отличается от первоначальной тем, что требуется оценить количество настройщиков фортепиано во всем мире (а не только в Чикаго). Вам для этого не нужны какие-либо статистические данные о настройщиках или фортепиано. Профессиональные пианисты не знают, сколько этих инструментов существует в мире. Однако вам нужно иметь представление о численности населения Соединенных Штатов и мира. Вам также разрешат округлять числа, потому что большую часть расчетов вам придется делать в уме. (Хотя есть и исключения. Бухгалтерские фирмы, банки и консалтинговые фирмы обычно разрешают вам пользоваться при расчетах карандашом и бумагой и ожидают от вас более точного ответа, чем компьютерные и интернет-компании.)

Вот типичный анализ: количество настройщиков должно быть связано с тем, сколько есть для них работы. А это, в свою очередь, зависит от количества фортепиано и от того, как часто их требуется настраивать.

Сколько же в мире пианино? В Соединенных Штатах они есть в школах, филармонических обществах, церквах, барах, студиях грамзаписи, музеях и многих других местах. Тем не менее большинство этих музыкальных инструментов все же находится дома у жителей страны.

Пианино дороги и громоздки — их трудно разместить в небольших квартирах, общежитиях или передвижных домиках-трейлерах. В основном пианино можно обнаружить только в домах представителей среднего и высшего класса.

Население США — это примерно 300 миллионов человек. Предположим, что типичная семья состоит из трех человек. Это значит, что в стране 100 миллионов домохозяйств. Наиболее богатая половина из них, то есть 50 миллионов семей, — целевой сегмент для продажи пианино. Конечно, не у всех из этих семей есть пианино. Доля состоятельных семей, у которых есть этот музыкальный инструмент, очевидно, менее 100 процентов и более одного процента. Предположим, что среди состоятельных семей 10 процентов имеют пианино — это означает, что в США есть пианино у 5 миллионов семей. Именно это число мы и будем использовать для нашей оценки.

Сколько настройщиков нужно, чтобы настраивать 5 миллионов пианино? Допустим, что настройщик пианино в среднем работает 40 часов в неделю (этот ведь не компьютерный бизнес!). Сколько времени нужно, чтобы настроить один инструмент? Приблизительная догадка — один час. Но клиенты не приходят со своими пианино в мастерскую, следовательно, настройщик потратит в среднем час на дорогу к клиенту. Это значит, что настройщик в среднем сможет настраивать 40/2 = 20 пианино в неделю. За год, состоящий из 50 рабочих недель, это дает приятную круглую итоговую цифру — 1000 настроенных пианино.

Как часто необходимо настраивать пианино? Этот вопрос может оказаться неразрешимым для тех, кто ничего не знает о пианино. Догадка «с потолка» (раз в год?), вероятно, достаточно близка к истине. Поиск в Интернете позволил найти рекомендацию настраивать пианино четыре раза в первый год после покупки и по крайней мере дважды в год в последующие годы. Эта рекомендация очень похожа на другие подобные (вроде пережевывать пищу двадцать шесть раз перед тем, как ее проглотить), которые никто (за исключением настройщиков пианино) не принимает всерьез. Наверняка в гостиных стоит немало пианино, которые почти никогда не используются, и их не настраивают годами.

Если нужно настраивать пианино раз в год, настройщик может настроить за год 1000 инструментов, то, вероятно, на каждую тысячу пианино придется один настройщик. Если учесть, что в Соединенных Штатах примерно 5 миллионов пианино, то настройщиков в этой стране должно быть около 5000.

Америку во многих отношениях, нельзя считать типичной страной — количество настройщиков пианино в этом плане не является исключением. Учитывая, что США — богатая страна с европейскими музыкальными традициями, можно предположить, что доля настройщиков пианино, которая приходится на США, больше, чем процент мирового населения, проживающий в этой стране. Мировое население — шесть миллиардов человек — в 20 раз больше, чем население США. Наверное, общее количество настройщиков пианино в мире в несколько раз больше, чем в США, но уж никак не в двадцать раз. Вполне реальная догадка может быть такой: в Европе может быть в два раза больше настройщиков, чем в США, а во всем остальном мире — примерно столько же, сколько в США. Это значит, что примерно каждый четвертый настройщик пианино живет в США. Оценка общего количества настройщиков пианино в мире будет такой: в четыре раза больше, чем 5000, или 20 000 настройщиков.

Именно такой ответ рассчитывают услышать интервьюеры. Насколько он точен? У мировой Гильдии настройщиков фортепиано примерно 3500 членов во всем мире. Хотя не все настройщики входят в гильдию и не все ее члены работают исключительно настройщиками. Бюро статистики занятости США сообщает, что в стране в 1998 году было примерно 13 тыс. человек, занимающихся настройкой и ремонтом музыкальных инструментов, большинство из которых работает с пианино.

Статистика продаж, которую можно найти в Интернете, показывает, что в Соединенных Штатах производится примерно 23 процента всех пианино, выпускаемых в мире, и покупается 27 процентов всех пианино, изготовленных в мире.[135] Если предположить, что примерно 10 тыс. настройщиков пианино, проживающих в США, — это четверть от общего количества настройщиков в мире, то в мире должно быть около 40 тыс. настройщиков — в два раза больше, чем мы предположили выше (это совсем неплохой результат для ответа на вопросы Ферми). Заниженная оценка может объясняться тем, что большинство людей, которые названы в статистических данных настройщиками, на самом деле занимаются также ремонтом и реставрацией музыкальных инструментов. Это значит, что потребность в их услугах выше, чем предполагалось, а отсюда и больше «настройщиков пианино».

Сколько всего бензоколонок в Соединенных Штатах?

Интервьюеры Microsoft также спрашивают кандидатов о том, сколько всего автомобилей в Соединенных Штатах. Решение этой задачи требуется для того, чтобы ответить на вопрос о количестве бензозаправочных станций, поэтому мы будем решать сразу обе задачи.

У детей, людей, живущих в городах с хорошим общественным транспортом, бездомных, членов религиозной секты Амиш и т. д. нет автомобилей. С другой стороны, есть люди, у которых более одной машины: это богатые люди, коллекционеры автомобилей, водители такси, у которых есть и автомобиль для работы, и второй автомобиль для личных надобностей.

Значит ли это, что на каждого жителя США приходится один автомобиль? Нет. А на каждых двух жителей? Это уже более вероятно. В таком случае, если учесть, что население США — это 300 миллионов человек, то в стране должно быть около 150 миллионов автомобилей.

Средний автомобиль заправляют примерно раз в неделю. Поэтому за неделю бензозаправочные станции обслуживают примерно столько же автомобилей, сколько их всего есть в стране.

Сколько примерно автомобилей может обслужить за неделю одна заправочная станция? Количество часов в неделе равно 24х7, но нe все бензоколонки работают круглосуточно. Допустим что типичная бензоколонка работает примерно сто часов в неделю. Если на заправку одной машины уходит шесть минут, то каждый из насосов заправочной станции может за час заправить десять автомобилей. Теперь нужно учесть, что на большой бензоколонке, расположенной в бойком месте, может быть много насосов, и, напротив, есть такие заправки, на которые клиенты заезжают редко. Давайте предположим, что среднее количество машин, которые заправляются на одной заправке в течение часа, — это десять. Тогда в среднем на одной бензоколонке за неделю будет заправляться 100 х 10, или 1000 автомашин.

Это значит, что количество бензозаправочных станций в США 150 миллионов / 1000 = 150 000.

Такие оценки количества бензоколонок и автомобилей достаточно точны. Министерство транспорта США сообщало, что в 1997 году в Соединенных Штатах было 129 748 704 «зарегистрированных пассажирских транспортных средства». В июньском номере за 1998 год журнала Journal of Petroleum Marketing утверждается, что в том году в США было 187 097 бензоколонок, которые продавали топливо для автомобилей.

Какое количество воды река Миссисипи проносит в течение часа мимо Нового Орлеана?

Возможно два подхода. Первый предполагает прямую оценку ширины реки Миссисипи около Нового Орлеана, ее средней глубины и скорости течения реки. Если вы можете оценить эти числа в футах и футах в час, то все, что вам нужно сделать, — это перемножить эти три числа для того, чтобы получить ответ (в кубических футах в час). Однако большинство людей (может быть, только за исключением тех, кто живет в дельте Миссисипи) не имеет ни малейшего представления об этих числах.

Второй подход подразумевает оценку площади водосбора реки. Вы можете знать или оценить, посмотрев на карту, что река Миссисипи со своими притоками собирает осадки примерно с половины территории Соединенных Штатов (и небольшого участка территории Канады). Оцените эту площадь и умножьте ее на среднее количество осадков для данного региона. Это даст вам объем воды, которая выпадает на этой площади в виде осадков в течение года. Почти вся эта вода в конце концов попадает в Миссисипи, за исключением той воды, которая испаряется. Вы должны сделать на это поправку, и большинство людей абсолютно не подозревает, какого порядка эта поправка должна быть.

Начнем с первого подхода, который кажется более простым. По крайней мере нужно найти всего три числа.

Насколько широка река Миссисипи в Новом Орлеане? На подробных картах нижнее течение реки Миссисипи изображается не синей линией — оно скорее похоже на озеро. Предположим, что ширина этого «озера» примерно две мили. Тогда в футах у нас получается удобная «круглая» цифра — 10 тыс. футов.

В воде Миссисипи очень много примесей, которые выпадают в виде осадков в дельте реки. Поэтому маловероятно, что река в дельте глубока. Кроме того, русло реки в ее нижнем течении не раз менялось — это бы вряд ли произошло, если бы река была глубокой.

Итак, река мелкая. Но насколько мелкая? Один фут? Десять футов? Сто футов? Вряд ли это один фут.

Если бы река была такой мелкой, ее можно было бы легко переходить вброд, и вы бы услышали об этом «удивительном факте»: мол, глубина Могучей Миссисипи — всего один фут.

10 футов (чуть больше трех метров) — это также мелко, но более вероятно. Специалисты по английской филологии, которые хотят стать менеджерами программ в Microsoft, могут припомнить, что «Марк Твен» («mark twain») на жаргоне речников во времена писателя означало «отметка два», или глубину в 12 футов (примерно 3,7 метра). «Марк Твен» также означало, что глубина достаточна для свободного прохода речных судов. Это была важная информация, потому что во многих местах Миссисипи была более мелкой. Так что десять футов — это вполне приемлемая оценка.

Последний параметр, который нужно оценить, — это скорость течения реки. Еще раз вспомните о речных судах. Даже после появления паровых двигателей они оставались медлительным транспортным средством по сравнению с автомобилями. Реалистичная оценка скорости течения — 10 миль в час. Это примерно 50 тыс. футов в час. Таким образом, ответ на задачу: 10 000 х 10 х 50 000 = 5 миллиардов кубических футов воды в час.

Реальный сток воды Миссисипи трудно измерить, и он существенно зависит от времени года и количества осадков. В энциклопедии Encarta, которая издается корпорацией Microsoft, приводится такая уверенная оценка с точностью до трех знаков — 593 тыс. кубических футов воды в секунду. Еще один авторитетный веб-сайт предлагает оценку в 14 тыс. кубических метров в секунду. Это примерно 490 тыс. кубических футов в секунду. В других источниках приводится более консервативная оценка — 1 миллион кубических футов в секунду. Это эквивалентно 3,6 миллиарда кубических футов воды в час.

Сколько весит весь лед на хоккейном катке?

Хоккейный каток имеет размеры примерно 100 на 200 футов. Его толщина — примерно один дюйм. Давайте все переведем в дюймы: 1000 х 2000 х 1 — в итоге получаем 2 миллиона кубических дюймов льда.

Сколько весит кубический дюйм льда? Немного меньше, чем кубический дюйм воды. Вероятно, легче будет вести расчеты в метрической системе. Кубический сантиметр воды весит один грамм. Дюйм — это примерно 2,5 сантиметра, таким образом, один кубический дюйм (мы специально округляем для приблизительных расчетов в уме) — это 2хЗх2,5 = 3x5 = 15 кубических сантиметров. Это значит, что объем льда на катке — это 15x2 миллиона = 30 миллионов кубических сантиметров и его вес — такое же количество граммов, или 30 000 килограммов, или 60 000 фунтов.

По правилам НХЛ, хоккейный каток — это овал 85 на 200 футов с закругленными углами радиусом 28 футов. Толщина льда обычно один дюйм. Если вы используете эти точные цифры для вычислений, то вес воды, необходимой для заливки льда на катке этих размеров, можно оценить в 38 500 килограммов, но, учитывая меньшую плотность льда по сравнению с водой, его вес будет меньше — примерно 35 200 килограммов. Как видите, наша догадка была достаточно близка к этой цифре.

Если вам придется упразднить один из пятидесяти штатов США, какой штат вы выберете?

Популярные ответы: Аляска, Гавайи, Северная Дакота.

Плохой ответ: Вашингтон.

Самый плохой ответ: Я бы упразднил все.

Это один из самых известных примеров неточно сформулированных задач, используемых Microsoft. Это не то же самое, что спросить, какой у вас любимой цвет. Они хотят, чтобы вы так переформулировали вопрос, чтобы на него стало возможным дать «правильный ответ», который можно было бы найти при помощи логики.

От вас не требуется дать ответ с ходу. Вы можете представить интервьюеру свой ход рассуждений и только в самом конце выбрать штат. Вот обсуждение и обобщение подходов, которые получили одобрение интервьюеров.

Центральный вопрос: что произойдет с людьми, которые живут в упраздненном штате? Мы собираемся сбросить на него атомную бомбу? Пускай вариант (а) — это такая ситуация, когда, «упраздняя» штат, мы уничтожаем и все его население. Тогда у нас появляется моральное обязательство минимизировать людские потери.

Вариант (b) — население просто «исчезает». Их не убивают — их просто больше нет на свете. Может быть, это похоже на ситуацию из известного фантастического рассказа, в котором некто отправляется в прошлое и наступает на бабочку… а потом возвращается и обнаруживает, что штат, из которого он отправился в путешествие во времени, и его население исчезли и просто никогда не существовали. На всех флагах — только сорок девять звезд, а исчезнувший штат не упоминается ни в одной из энциклопедий.

Вариант (с) — исчезает только недвижимость, а люди уцелели. Эти уцелевшие люди, ставшие бездомными беженцами, сидят около огромной дыры, оставшейся на месте исчезнувшего штата, и раздумывают о том, где они будут сегодня ночевать. Этих людей придется переселять, что обойдется недешево (корпорации Microsoft. Федеральному правительству?).

Вариант (d) — люди «магическим способом» переносятся в какое-то другое место безо всяких эмоциональных или финансовых издержек. Просто нажимается кнопка, и все бывшие жители упраздненного штата получают дом и работу (предполагается, что они у них были и раньше) в каком-то из сохранившихся сорока девяти штатов, причем права «старожилов» штата, который станет для них рбдньгм, никак не ущемляются.

Вариант (е) — не исчезают ни люди, ни недвижимость. «Упразднение» штата — это чисто политическое решение. Упраздненный штат присоединяется к Канаде или Мексике или становится независимым государством.

Выбор в случае (а) достаточно очевиден. Если люди погибнут, то вы должны выбрать самый малонаселенный штат. Согласно переписи 2000 года, таким штатом был Вайоминг.

Вариант (b) — это тяжелый случай. Люди просто исчезают непонятно как, и для решения нет никаких моральных ориентиров. И все же эти люди — живые души, пока вы не нажмете на кнопку вашего «упразднителя истории». Это все равно очень похоже на убийство, и снова нужно, вероятно, выбирать Вайоминг.

Дилемма в случае (с) заключается в том, стоит ли подумать о выборе более населенного, чем Вайоминг, штата, учитывая природные красоты последнего. Вайоминг — это большой штат с красивым ландшафтом, и именно там расположен Йеллоустонский национальный парк с его знаменитыми секвойями. Чтобы все это сохранить, вы можете предпочесть переселить жителей более населенного, но меньшего по размеру и/или менее живописного штата.

По данным переписи 2000 года, пять штатов с наименьшим населением — это Вайоминг, Вермонт, Аляска, Северная Дакота и Южная Дакота. Вермонт и Аляска — тоже живописные штаты, кроме того, Аляска обладает огромной территорией. В Южной Дакоте есть гора Рашмор. В Северной Дакоте… да, в Северной Дакоте нет горы Рашмор. Этот штат «выделяется» среди других тем, что трудно представить себе жителя какого-то другого штата, который сознательно решил бы провести в Северной Дакоте свой отпуск (есть даже такая шутка: дерево, символизирующее Северную Дакоту, — это телеграфный столб). Да и другие равнинные штаты не могут похвастаться интересным рельефом или лесами, но в Северной Дакоте кроме всего прочего еще и самая суровая зима — даже более суровая, чем в наиболее населенных районах Аляски.

Итак, в варианте (с) — никого не убивают, но нужно платить за переезд людей из упраздненного штата. Конечно, стоит пойти на несколько большие расходы, но сохранить Йелоустон, или лыжные курорты Вермонта, или Аляску, или гору Рашмор. Без Северной Дакоты можно обойтись.

В варианте (d) перевозка населения проводится при помощи магии и абсолютно бесплатна — тем больше причин упразднить именно Северную Дакоту.

Наконец, в варианте (е) сохраняются и люди, и территория. Мы просто меняем политическую карту. Тут стоит подумать об Аляске и Гавайях. И тот, и другой штаты отделены от основной материковой территории США. Некоторые люди скажут, что сохранение этих территорий — это наследие колониализма. Если вас в первую очередь интересует, как выглядят страны на географических картах — стоит выбрать или Аляску, или Гавайи.

Но признайте: если Конгрессу действительно придется обсуждать решение, какой из штатов упразднить, — географические соображения будут учитываться в последнюю очередь. Аляска богата нефтью и полезными ископаемыми. Гавайи — это то место, куда отправляются проводить отпуск жители континентальных штатов США. Оба эти штата стратегически важны. Поэтому об их упразднении не пойдет и речи.

Как и в вариантах (с) и (d), выбор будет сделан между штатами, которые уступают другим по численности населения и богатству природных ресурсов. Так что опять всплывет Северная Дакота, которая к тому же расположена на границе с Канадой. Предложите этот штат Канаде, а если Канаде он не нужен, что ж, пускай Северная Дакота станет независимым государством.

Сколько мест на земном шаре, где, если вы пройдете одну милю на юг, одну милю на восток и одну милю на север, вы вернетесь в то место, откуда вы отправлялись в путь?

Система оценок, которую используется Microsoft для оценки ответов на этот вопрос, примерно такова:

0 таких мест — не принимать на работу;

1 такое место — не принимать на работу;

бесконечно + еще одно место — удовлетворительно;

бесконечно х бесконечно + еще одно место — правильный ответ.

Начнем с воображаемой карты: одна миля на юг, одна на восток и одна на север — это три стороны квадрата. Вы окажетесь в точке, которая будет расположена на одну милю восточнее, чем ваше место старта. Эта ситуация может вам показаться неразрешимой, и вы поспешите заявить, что таких мест на земле нет.

Попробуйте-ка еще один раз. Единственный способ разрешить эту ситуацию — вспомнить о том, что направление, которое указывает стрелка компаса, — это явление относительное, поскольку мы живем на поверхности сферы. На Северном полюсе любое горизонтальное направление указывает на юг. Если вы стартуете на Северном полюсе, вы можете пройти милю в любом направлении, и это будет считаться движением на юг. Более того, следующая миля пути на восток будет расположена по окружности вокруг Северного полюса. У вас получится именно так, если вы не только изначально направитесь на восток, но и будете постоянно корректировать свое направление движения, чтобы все время идти строго на восток. Тогда у вас будет возможность на финальном отрезке идти прямо к Северному полюсу и вернуться туда, откуда вы отправились. Таким образом, ваш маршрут будет напоминать «треугольный кусок пирога», а не разомкнутый квадрат.

Итак, первая возможная точка — это Северный полюс. Обратите внимание на то, что Южный полюс для решения этой задачи не подходит. На Южном полюсе любое направление ведет на север, поэтому там вы просто не сможете двигаться на юг.

Вы можете решить, что правильный ответ — есть одно такое место, и вы снова будете не правы. Не правы потому, что такой маршрут может начаться и в точке, расположенной поблизости от Южного полюса. Представьте, что вы стартуете в точке, которая расположена на расстоянии чуть больше мили от Южного полюса. Вы пройдете одну милю на юг, потом повернете на 90 градусов и отправитесь на восток, при этом вы опишете полную окружность длиной в одну милю вокруг полюса, направляясь все время строго на восток, и, наконец, пройдете милю на север и вернетесь в исходную точку.

Такая точка не одна — таких точек бесконечное количество. Вы можете отправиться из любой точки, которая находится на подходящем расстоянии от Южного полюса. Такие точки расположены на окружности, центр которой — Южный полюс.

Что такое «подходящее расстояние»? Окружность длиной в одну милю должна иметь радиус 1/2Пи мили. Стартовая точка маршрута должна располагаться еще на одну милю дальше от полюса, то есть на расстоянии в 1+1/2Пи мили от него, или примерно в 1,159 мили.

Но и это еще не все. Допустим, вы стартуете чуть ближе к полюсу. Вы идете одну милю на юг, а потом идете строго на восток по меньшей окружности, длина которой 1/2 мили. Вы дважды совершите полный круг, а потом пройдете еще одну милю на север и вернетесь в исходную точку. Таких точек опять-таки бесконечное множество, и они расположены на расстоянии в 1 + 1/4Пи мили от полюса.

Вы также можете выбрать такой маршрут, чтобы на втором этапе пройти вокруг полюса три раза, четыре раза и вообще любое целое число Пи раз. Каждый раз эти точки также будут расположены на окружности, центр которой полюс, а радиус — 1 + 1/2Пи мили. Таким образом, подобных точек — бесконечное множество, и расположены они на бесконечном количестве окружностей, расположенных концентрически вокруг полюса.

Эта задача — вариация на тему одной из самых известных в мире головоломок. В ней путешественник проходит удовлетворяющий решению задачи маршрут и по пути убивает медведя. Нужно ответить на вопрос о том, какого цвета был медведь. Ответ — это был белый медведь, так как у Северного полюса живут только белые медведи. В конце 1950-х годов Мартин Гарднер написал, что «недавно один человек понял, что Северный полюс — не единственный правильный ответ на эту старинную загадку».[136] На самом деле «новые» ответы не подходят для старинной головоломки, потому что в Антарктике нет наземных млекопитающих, включая медведей.

Сколько раз в течение суток перекрываются часовая и минутная стрелки?

Большинство людей сразу же понимает, что ответ должен быть 24 плюс-минус. Все проблема как раз в том, чтобы вычислить этот плюс-минус.

Сначала обратите внимание, что перекрытие стрелок — это абсолютно предсказуемое явление. Обе стрелки движутся с постоянной скоростью, следовательно, интервал времени между двумя последовательными перекрытиями постоянный.

Этот постоянный интервал чуть более часа. В полночь часовая и минутная стрелки точно совпадают. Минутной стрелке требуется ровно шестьдесят минут, чтобы описать полный круг, за то же самое время часовая стрелка проходит 1/12 часть круга и находится на отметке 1 час. Чтобы добраться до отметки 1 час, минутной стрелке потребуется пять минут, но за это время часовая стрелка еще немного продвинется вперед…

Перед тем как увлечься обсуждением парадокса Зенона[*], давайте пока предположим, что между последовательными перекрытиями стрелок проходит чуть больше, чем 65 минут. Мы также знаем, что если умножить этот точный интервал на неизвестное целое число, должно получиться ровно двадцать четыре числа, так как каждые двадцать четыре часа часовая и минутная стрелки точно перекрываются на отметке 12. На самом деле это происходит каждые двенадцать часов — ведь путь, который стрелки проходят с полуночи до полудня, точно совпадает с путем, который они проходят с полудня до полуночи.

Давайте подробно проанализируем, что происходит за двенадцать часов с полуночи до полудня. За этот период стрелки не могут совпасть двенадцать раз — в этом случае интервал между совпадениями стрелок был бы 12/12 — или ровно один час, а мы знаем, что на самом деле он чуть больше, чем 65 минут. Следовательно, за этот период стрелки могут совпасть лишь 11 раз. Это значит, что продолжительность интервала между перекрытиями стрелок 12/11, или 65,45 минуты. Это и должен быть точный интервал, который мы не смогли вычислить чуть ранее. Умножив одиннадцать на два, мы получаем двадцать два перекрытия стрелок за двадцать четыре часа. Таким образом, двадцать два — это точный ответ, если только вы не захотите учитывать и совпадение стрелок в начале суток в полночь и в конце суток в следующую полночь — в этом случае ответом будет двадцать три.

У Майка и Тодда есть 21 доллар на двоих. У Майка на 20 долларов больше, чем у Тодда. Сколько денег у каждого? В ответе нельзя использовать дроби.

Это вопрос с подвохом, в котором скрыт «вызов». Ответ на основной вопрос достаточно прост. У вас может возникнуть искушение ответить, что у Майка 21 доллар, а у Тодда — 1 доллар, но тогда получается сумма в 22 доллара. Правильный ответ должен быть таким: у Майка 20,50 доллара, а у Тодда — 0,50 доллара. Если это для вас не очевидно — вы можете использовать алгебру, составить и решить уравнение. Вы также можете доказать, что это — единственный правильный ответ, но интервьюер настаивает, что в ответе нельзя использовать дроби.

Интервьюер не прав (или использует «техническую тонкость»: мол, целое количество центов — это не дроби). Ожидается, что вы будете отстаивать свою точку зрения и доказывать, что правильный ответ именно $20,50/$0,50. Такова жизнь в больших организациях.

Сколько в среднем раз вам нужно открыть наугад телефонный справочник Манхэттена, чтобы найти нужный вам номер телефона?

«Открыть наугад» подразумевает, что вы случайно открываете двухстраничный разворот книги (вы не должны пытаться использовать знания о том, какой букве алфавита соответствует нужный вам номер телефона). Подразумевается также, что, если нужный вам номер есть где бы то ни было на двух случайно открытых вами страницах, вы его обязательно найдете.

Есть и простой ответ, и более изощренный.

Вот простой ответ. Допустим, в телефонном справочнике Манхэттена одна тысяча страниц (это достаточно точная оценка: в издании этого справочника 2001 года было 1138 страниц. Вы можете игнорировать тот факт, что в начале и конце телефонной книги есть страницы, на которых нет номеров телефонов). Это значит, что в телефонной книге 500 разворотов. Таким образом, вероятность, что книга откроется в нужном вам месте в первый и в любой последующий раз, — один из пятисот.

Этот быстрый ответ вполне приемлем, учитывая, что самый уязвимый пункт в ваших рассуждениях — это догадка о количестве страниц в телефонном справочнике.

А теперь ответ, удовлетворяющий людей из «математического лагеря». В реалистической ситуации вам, наверное, захотелось бы узнать, сколько раз вам нужно случайным образом раскрыть телефонную книгу, чтобы быть уверенным с заданной вероятностью, что хотя бы один раз она раскроется на нужной вам странице. Допустим, вы хотите быть уверенными, что в 90 процентах случаев отыщете нужный вам номер. Сколько раз для этого нужно раскрыть телефонный справочник?

Поскольку это случайная процедура, абсолютных гарантий нет. Вам может повезти, и тогда вы найдете нужный номер на первой же странице, и, наоборот, вы можете миллион раз перелистывать книгу и ни разу не открыть ее на нужной странице. Если вы хотите быть на 100 процентов уверенными, то ответ прост: сколько бы раз вы ни открывали случайным образом телефонную книгу, вы никогда не можете быть уверены на 100 процентов, что она хотя бы раз откроется на нужной странице.

В общем, вам придется снова и снова раскрывать справочник, пока он открывается на ненужных вам страницах. Поэтому мы можем анализировать вероятность того, что телефонная книга будет раз за разом раскрываться на ненужных страницах.

Допустим, вам известно, что в справочнике точно 1000 страниц и 500 разворотов. Вероятность того, что вы раскроете книгу на неправильной странице в каждой из попыток — 499 из 500, так как из 500 возможных разворотов книги только один подходящий. Тогда вероятность того, что в n последовательных попытках телефонная книга каждый раз будет раскрываться на неверных страницах — (499/500)n .

Очевидно, что вероятность того, что вы откроете книгу на нужной странице за n последовательных попыток или раньше, будет равна выражению: 1—(499/500)n .

Эта формула позволяет вам вычислить, сколько раз вам нужно случайным образом раскрыть телефонную книгу, чтобы она с заданной вероятностью раскрылась на нужной вам странице. Если вы сделаете расчеты, например в Excel, то увидите, что для 50-процентной уверенности вам нужно раскрыть телефонный справочник 347 раз (или меньше, если вам повезет). Это число попытки и можно назвать «средним».

С другой стороны, этот ответ можно считать оптимистическим. Если вы сделаете 347 попыток — шансы на успех будут только 50 на 50.

Первоначальная оценка, которая была получена при помощи простого метода, — 500 попыток дают вероятность успеха 63 процента. Для того чтобы достигнуть 90-процентной вероятности успеха, вам нужно случайным образом раскрыть книгу 1150 раз.

Как можно разрезать прямоугольный торт на два равных куска, если кто-то уже вырезал из него прямоугольный кусок?..

Есть два правильных ответа, и лучше, если вы дадите их оба. Более простой ответ находят реже, чем сложный.

Можно очень легко разрезать прямоугольник пополам — вам нужно только позаботиться о том, чтобы разрез прошел через его центр, причем под любым углом.

В данном случае у нас два прямоугольника: «позитивный» (то, что пока осталось от торта) и «негативный» (недостающий кусок). Найдите центры обоих прямоугольников и проведите через них прямую линию — это и будет линия разреза. Вы получите два равных куска.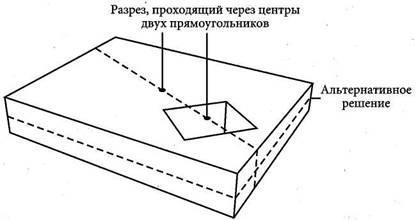

Поскольку разрез проходит через центры обоих прямоугольников, площадь двух кусков будет такова: половина площади торта минус половина площади вырезанного из торта куска. Другими словами, площадь двух кусков будет одинаковой. Это будет верным, несмотря на то, что форма кусков может быть различной.

В маловероятном случае, когда центры обоих прямоугольников оказались в одной и той же точке, можно делать разрез в любом направлении, но он, конечно, должен проходить через центр.

Альтернативное решение — резать торт не вертикально, а горизонтально, чтобы получить куски, толщина которых будет в два раза меньше, чем у целого торта, и в каждом не будет хватать одинакового по форме и площади куска. Это решение, конечно, не подходит, если торт сверху покрыт глазурью.

Какой дизайн вы предложите для туалетной комнаты Билла Гейтса?

Для ответа наэтот вопрос нужно учесть два важных обстоятельства. Во-первых, Билл Гейтс всегда может позволить себе получить то, что хочет. Во-вторых, вы должны по крайней мере предложить какие-то идеи, которые могут понравиться Гейтсу, хотя он сам об этом пока не задумывался (иначе какой смысл нанимать вас для дизайна его туалетной комнаты?).

Подразумевается, что вы усядетесь где-то вместе с Гейтсом и выслушаете, какой бы он хотел видеть свою туалетную комнату. Он сообщит вам о бюджете и сроках. Вы предложите ему много разных идей и узнаете его мнение о них. Потом вы составите план и подадите его на утверждение Гейтсу. Этот план придется не раз пересматривать, а вы, несмотря на это, должны позаботиться о том, чтобы проект уложился в срок и бюджет не был превышен. Это относится к любой задаче на разработку дизайна.

Что касается конкретных идей, которые вы предложите, имейте в виду, что вам будет трудно превзойти то, что у Гейтса уже есть в реальности. Ванная Билла Гейтса устроена так, что он может, не выходя из машины, послать команду и заполнить ее водой нужной температуры. На самом деле!

Компьютеризировать весь свой дом — это идея, к которой люди из Microsoft относятся очень серьезно. Исследовательские подразделения Microsoft разрабатывают «умные» шкафчики для лекарств и туалетных принадлежностей, которые сообщат вам, что у вас заканчивается нужное вам лекарство или туалетная бумага. «Некоторые из этих „сценариев будущего“ могут показаться очень странными, признает Тед Куммер, вице-президент Microsoft по программе MSN Internet Access. — Ну, например, унитаз, который следит за здоровьем всех членов семьи, делая регулярные химические анализы, шкафчик для лекарств, который помогает заказать номер в гостинице или запереть вашу машину в гараже».[137]

Поэтому, если вы хотите удивить интервьюеров из Microsoft, вам вряд ли удастся это сделать, рассуждая об унитазах с электрическим подогревом. Вот несколько идей, которые им могут понравиться (это идеи футуристические, но уже сегодня их могут позволить себе богатые потребители, для которых деньги — не вопрос).

— Устройство, которое автоматически запирает шкафчики с лекарствами или средствами бытовой химии, когда в ванную входит ребенок без присмотра взрослых. В доме Гейтса уже можно отслеживать, кто находится в той или иной комнате. Идет разговор о сканировании радужной оболочки глаза и других способах быстрой и незаметной идентификации людей. Это как раз и может помочь запирать шкафчик с лекарствами от детей, «если это позволит спасти жизнь хотя бы одному ребенку», и т. д. и т. п.

— Блокнот для заметок, к которому не нужно прикасаться руками. Каждому человеку иногда приходят в голову хорошие идеи, когда он находится в туалете. Вам не захочется прикасаться к своей электронной записной книжке-«наладоннику» мокрыми руками, и если в доме Гейтса и есть такая комната, где нет компьютера, так это, наверное, туалет. Все, что вам нужно, — это устройство распознавания голоса, которое сможет записать ваше сообщение после того, как вы произнесете кодовую фразу, например «Заметки для Билла». Это устройство может автоматически отсылать записанную информацию по электронной почте к вам на работу.

— Зеркало, которое не меняет местами право и лево. Это видеоэкран и скрытая видеокамера, которые будут показывать ваше изображение таким, каким его видят другие люди, глядящие на вас. Вам будет гораздо легче пользоваться ножницами, чтобы, например, отстричь выросший не на месте волосок или подравнять усы. Если вы думаете, что эти незначительные преимущества вряд ли оправдывают отказ от «низкотехнологичного» решения, которое работает безотказно, не нуждается в новом программном обеспечении и будет работать, даже если отключится электричество… Ну, вы уверены, что действительно хотите работать в Microsoft! (У Гейтса была идея, что репродукции произведений искусства на жидкокристаллических экранах, которые вы увидите повсюду в его доме, если на них никто не смотрит, должны сливаться с деревянной отделкой стен, имитируя и фактуру дерева. Этого так и не удалось добиться. Все закончилось тем, что Гейтс заказал у столяров скользящие деревянные панели, которые могут закрывать видеоэкраны.)

Другие компании — производители программного обеспечения стали также задавать кандидатам на работу вопрос о туалетной комнате. Они, правда, часто варьируют пол и физические размеры главного героя: «Какой дизайн вы предложите для туалетной комнаты, которой будет пользоваться богатая дама, весящая сто пятьдесят килограммов?»

Как вы сконструируете микроволновую печь, управляемую компьютером?

Легко понять, что микроволновая печь и компьютер — не самая великая пара, которая может стать наследницей великих танцовщиков Фреда Астера и Джинджер Робертс. Многие вопросы о дизайне именно таковы: вам дают какую-нибудь сомнительную идею и просят на ее основе сконструировать что-нибудь по возможности не очень глупое.

Микроволновыми печками теперь довольно просто управлять. Пользователям, наверное, не понравятся новшества, которые усложнят управление (но вам стоит сказать, что вы проведете исследование мнений потребителей для проверки — это почти всегда ожидается, когда вам зададут вопрос о дизайне). По ряду намеков интервьюеров Microsoft можно понять, что они имеют в виду «умную упаковку»: на бытовых приборах и кухонной мебели можно установить сенсоры, которые будут считывать информацию со специальных ярлыков и штрих-кодов, помещенных на упаковке продуктов. Если речь идет о микроволновке — вы можете положить в нее замороженную лазанью, а она сама «прочтет» код с инструкциями по размораживанию (или загрузит их из Интернета). Она также автоматически установит мощность и сделает нужные поправки (учтет размер упаковки, температуру полуфабриката и т.п.). Вам уже никогда не понадобится вручную устанавливать время и другие параметры.

«Умная» упаковка позволит микроволновке хранить данные обо всей приготовленной еде. Это важно упомянуть, потому что анализ информации об использовании бытовых приборов в маркетинговых целях сейчас — популярная идея в Microsoft. С точки зрения потребителя, такой архив информации может быть полезен, чтобы планировать, какую еду нужно покупать на неделе, и учитывать количество съеденных калорий, если потребитель на диете.

Еще один хороший ответ — сказать, что программа распознавания голоса может сделать ненужными кнопки на микроволновке. Вместо того чтобы нажимать на них, вы сможете просто сказать вашей микроволновой печке, как долго она должна готовить какие-то продукты (допустим, овощи или рыбу — любые другие продукты, на которых нет кодовой информации), или вы можете сообщить микроволновке, что вы собираетесь готовить, а она сама определит, сколько времени это нужно готовить.

Какой дизайн вы предложите для пульта управления видеомагнитофоном?

Десятки талантливых промышленных дизайнеров работали над этой проблемой. Вряд ли вам удастся за пятнадцать минут их превзойти. Интервьюер и не ожидает от вас этого. Лучший способ начать ответ — показать, что вы понимаете, что есть несколько важных противоречий, которые необходимо учесть в дизайне. Вот два наиболее значимых.

1. Легкость использования или цена. Мы не меньше любим шутить по поводу людей, которые не знают, как запрограммировать свои видеомагнитофоны, чем по поводу ужасной еды, которую дают в самолетах (или ее фактического отсутствия)[138]. Но действительно ли мы хотим платить за что-то более привлекательное? Большинство людей покупает самый дешевый билет на самолет, а потом жалуется на плохое качество еды. Авиакомпании знают об этом, вот почему вы в лучшем случае получите от них горсточку пережаренного арахиса. Вполне возможно, что это верно и для рынка видеомагнитофонов. Люди покупают прежде всего из-за цены и меньше внимания обращают на качество, а потом жалуются, что пультом управления трудно пользоваться.

Сколько точно есть людей, готовых платить дополнительно за удобные пульты дистанционного управления видеомагнитофонами? Если это в основном богатые пенсионеры, у которых проблемы со зрением, — это одна история. А если это в первую очередь восьмилетние дети, у которых есть свой телевизор, и они хотели бы иметь еще и собственный недорогой видеомагнитофон — дизайн, очевидно, должен быть другим. А вот если окажется, что никто не хочет платить за более удобный в использовании пульт управления — это значит, что нужно вообще отказаться от этой идеи.

2. Легкость использования или дополнительные возможности. Вы можете сконструировать видеомагнитофон, который будет управляться при помощи всего одной кнопки. Вы нажимаете на эту кнопку и начинается запись, нажимаете на нее еще раз — запись останавливается. Вот он, видеомагнитофон, которым любому будет легко управлять.

Дополнительные функции нужны только в том случае, если вы хотите, чтобы видеомагнитофон записывал телепередачи, когда вас нет дома, чтобы их потом можно было просматривать. Маловероятно, что все захотят купить видеомагнитофон всего с одной кнопкой управления только потому, что им легко управлять. Сегодняшние производители снабжают видеомагнитофоны большим набором функций, которыми можно управлять при помощи пульта управления переключая его в нужный режим. Вы не можете просто ввести с помощью клавиатуры или выбрать время, когда видеомагнитофон должен начать запись — вместо этого вам придется долго нажимать на кнопки, устанавливая количество минут, часов, время до или после полудня, день, неделю. Это затрудняет программирование видеомагнитофона.

Чтобы упростить задачу, предположим, что маркетинговые исследования показали, что есть потребители, заинтересованные в покупке более легких в управлении видеомагнитофонов. Будет также полезно узнать, пользуются ли эти потенциальные покупатели всем набором функций, которыми обладает большинство современных видеомагнитофонов. Как часто обладатели видеомагнитофонов программируют их для записи за неделю до того, как программа появится в эфире? За двадцать четыре часа до показа? Если отказаться от некоторых функций, это может упростить интерфейс.

Вот грубый набросок того, как мог бы работать такой простой и удобный интерфейс: на корпусе видеомагнитофона всего пять кнопок (воспроизведение, пауза, прямая перемотка, обратная перемотка и смена кассеты). Это на самом деле только резервный пульт управления, на тот случай, если дистанционный пульт куда-нибудь «завалится». На корпусе видеомагнитофона не будет дисплея (в целях экономии). Все программирование выполняется при помощи дистанционного пульта и экранных меню. На пульте дистанционного управления только одна кнопка и «джойстик». Джойстик будет похож на устройства, которыми снабжаются некоторые ноутбуки и компьютерные мониторы. Они тоже похожи на кнопку, которую вы можете двигать в любом направлении, чтобы контролировать перемещающийся по экрану курсор. Кнопка на пульте — для выбора функций. По существу этот пульт — аналог компьютерной мыши.

Чтобы запрограммировать ваш магнитофон, вы берете пульт и нажимаете джойстик или кнопку. Это «пробуждает» видеомагнитофон (если он в данный момент не работает), и на экране телевизора появляется меню/помощник/панель управления. Такой интерфейс позволяет проигрывать записанные кассеты, записывать программы и устанавливать нужное время (если по какой-то причине вас не удовлетворяет автоматическая синхронизация). Видеомагнитофон будет загружать и показывать на экране телепрограмму, и вы будете просто выбирать нужные вам передачи и щелкать кнопкой пульта, чтобы они были записаны.

Поскольку основным маркетинговым преимуществом такого дизайна должна быть простота двухкнопочного управления, повышенное внимание нужно уделить внешнему виду пульта, его декоративному дизайну и приятным ощущениям при пользовании им. Он не должен быть похож на другие пульты. Если ваша целевая группа — молодые люди, он должен выглядеть «круто», например, как прозрачный компьютер iMac фирмы Apple. Если же основная целевая группа — пенсионеры, позаботьтесь о том, чтобы пульт и кнопки были удобными для тех, у кого пальцы уже не обладают былой подвижностью.

Разработайте дизайн пульта управления для подъемных жалюзи.

У обычных жалюзи два «устройства» для управления (обычно это просто два шнура) — одно их поднимает и опускает, а другое изменяет угол, под которым повернуты планки. Таким образом, пульт должен управлять этими двумя параметрами, возможно, при помощи двух кулисных переключателей.

Как только вы установите механизм для открывания и закрывания жалюзи, вы можете добавить функцию, позволяющую программировать эти процессы. Люди обычно не открывают и не закрывают жалюзи без причин. Они а) открывают их, чтобы было больше света; b) закрывают, когда солнце светит кому-то прямо в глаза или ковер может выцвести; с) закрывают их ночью, чтобы никто не подглядывал в окна.

Здесь нужно проанализировать то же противоречие между легкостью использования и разнообразием функций, что и в случае с видеомагнитофоном. Нужна ли вам возможность программировать жалюзи, подобно видеомагнитофону, чтобы они сами открылись в 7:30 утра, изменяли угол наклона планок в 16:45-17:05, чтобы вечернее солнце не светило вам в глаза и, наконец, закрывались жалюзи в 19:45? Наверное, нет. Как определить нужное время? Оно меняется в зависимости от времени года и погоды. В пасмурный день вы захотите полностью открыть жалюзи, чтобы в комнате было как можно светлее.

Лучшее решение — использовать фотоэлемент. По умолчанию жалюзи будут открываться, когда освещенность превысит какое-то значение (то есть днем), и закрываться, когда она будет ниже заданного значения (вечером и ночью). Фотоэлемент также подаст команду изменить угол наклона планок, чтобы затенить комнату, когда на жалюзи падает слишком яркий прямой солнечный свет. Нужные параметры можно будет задавать при помощи круглого циферблата, установленного на пульте (при помощи того же циферблата вы можете вообще отключить пульт управления, когда уезжаете в отпуск). Таким образом, на пульте будет круглый циферблат, чтобы задавать программы, и два кулисных переключателя для ручного управления жалюзи.

Предложите дизайн кухонной полочки для специй, которой будет пользоваться слепой человек.

Вы можете использовать ваш интеллект для того, чтобы переформулировать этот вопрос. Если вы твердо уверены, что больше подойдет не полочка, а круглый поворачивающийся поднос — так и говорите. Итак, мы с вами конструируем «интегрированную систему» для хранения и использования специй, которой будет пользоваться слепой человек. Почти во всех ответах упоминаются ярлычки для баночек с разными специями, на которых надписи шрифтом Брайля. Но здесь есть одна деталь: шрифт Брайля трудно читать на изогнутых поверхностях. Поскольку обычно баночки для специй цилиндрической формы, единственная плоская поверхность — это крышка такой баночки. Поэтому надписи должны быть именно на крышках — тогда можно скользнуть по ним пальцами, прочитать надписи и найти нужный вид специй.

У такого подхода есть ряд недостатков. Надписи будет легко прочитать, только если вы будете, возвращая баночку на полку, скрупулезно заботится о том, чтобы крышка была ориентирована в нужном направлении, в противном случае все надписи будут расположены под разным углом, и их будет трудно прочитать.

Вторая проблема связана с тем, что, когда люди готовят, они снимают крышки с баночек и не всегда возвращают их на место, поэтому их легко перепутать. Третья проблема связана с тем, что, когда баночки приносят из магазина, придется пересыпать специи из обычных баночек в специальные с надписями Брайля.

Может быть, стоит поместить надписи на сами баночки, а не на крышки? Тогда неважно, если крышки перепутаются. Но мы уже упоминали, что на изогнутых поверхностях трудно читать шрифт Брайля, кроме того, и баночку можно поставить на полку надписью к стене.

Эта проблема решается, если сделать баночки прямоугольного сечения и поместить надписи на каждой их стороне. Сама полочка должна быть такой, чтобы баночки на нее можно было ставить только ровно, а не под углом. Она также не должна закрывать то место на баночках, где помещается надпись — тогда можно будет легко ее прочитать, скользнув пальцами по лицевой стороне баночек. Выпуклые буквы шрифта Брайля, если ярлычки печатать на бумаге, быстро сотрутся от прикосновений к ним и пара, которого всегда много во время готовки. Лучше выдавить их прямо на стекле (или другом материале, из которого сделаны баночки). Но тогда не удастся использовать стандартные баночки, и это повысит стоимость. Более эффективное решение — использовать самоклеящиеся ярлычки из прочного и гибкого пластика. Тогда для них подойдут баночки любой формы.

А действительно ли вам нужны специальные баночки? Во многих отношениях легче использовать обычные баночки из супермаркета, но сконструировать полку так, чтобы они не путались. Допустим, на полке есть достаточное количество «гнезд» или просто отверстий для баночек, а на передней панели полочки, которая расположена под «эргономичным», оптимальным для чтения углом, — ярлычки с надписями шрифтом Брайля. Тогда, скользнув по этой панели пальцами, можно легко обнаружить нужную надпись и достать нужную баночку.

Из трех перечисленных возможностей (помещать ярлычки на крышках, на самих баночках или на полке) последняя — наиболее простая и, вероятно, лучшая. Но возможны и другие решения, если вы учтете ряд дополнительных соображений. На практике специи часто отмеривают ложкой. Слепому человеку трудно ею пользоваться. Допустим, вам нужно отмерить 1/8 чайной ложки — сколько специй у вас на самом деле в ложке? Для того чтобы это узнать, вы должны провести пальцем по поверхности насыпанных в ложку специй, высыпав лишнее обратно в баночку (как вы надеетесь), и, не дай бог, если вам действительно необходима именно 1/8! Для этой операции нужны обе руки, а это значит, что баночку и крышку нужно куда-то поставить — вам ведь не захочется обжигаться, отыскивая их на горячей плите.

Не правда ли, баночка, которая может сама отмерить нужное количество молотых специй (допустим, 1/8 чайной ложки), когда вы нажмете на кнопку, вам бы очень пригодилась? Такая конструкция баночки решает много проблем: вам не нужно снимать крышку (за исключением тех случаев, когда вы снова наполняете баночку, поэтому крышка не потеряется, и вы не обожжете руку, пытаясь ее отыскать). Вам также не нужно будет думать, куда же запропастилась дозировочная ложечка, догадываться, сколько в ней в самом деле специй, а потом ее мыть. Если все это учесть, то преимущества такой конструкции перевесят неудобства от необходимости пересыпать специи в эти дозировочные баночки из тех упаковок, в которых они продаются в супермаркете. Кстати, и зрячим людям дозировочные баночки могут показаться удобными.

Таким образом, удобный дизайн — это дозировочные баночки прямоугольной формы, на каждой из четырех сторон которых есть самоклеящиеся ярлычки из стойкого пластика с надписями шрифтом Брайля (тогда вам не надо беспокоиться о том, какой стороной вы поставили эти контейнеры на полку). Что касается самой полки, то она прежде всего должна быть сделана так, чтобы ярлычки помещенных на нее баночек было удобно читать, скользнув по ним пальцами. Стандартные полочки для специй обычно подвешивают на уровне глаз, чтобы было удобно читать мелкий шрифт названий специй. В данном случае более удобно разместить полочку на уровне пояса — как клавиатуру компьютера, так, чтобы надписи были расположены почти горизонтально под небольшим углом. Таким образом, баночки-контейнеры будут почти «лежать» на ней, но под небольшим углом, так, чтобы они не соскальзывали. В этом случае вам не понадобится ограждение на лицевой стороне полочки, и с нее будет легко снимать баночки-контейнеры.

Как бы вы стали тестировать солонку? (Тостер? Чайник? Лифт?)

Когда вам задается вопрос о тестировании, вам нужно вообразить, что у вас для этого такие же возможности, как у журнала Consumer Reports («Отчеты для потребителей»), публикующего отчеты о тестировании различных потребительских товаров, и ответить на вопрос интервьюера. Хорошие ответы — это не обязательно глубокие ответы. Вам нужно показать, что вам понятно: даже когда вы тестируете простые вещи, необходимо использовать несколько критериев (оценка достоинств автомобиля определяется не только максимальной скоростью, которую он может развивать, но и целым комплексом разнообразных факторов).

Один из возможных путей для ответа: представить себе, какие недостатки могут быть у объекта тестирования. Это довольно просто, если речь идет о лифте, но не так очевидно, если вам нужно тестировать солонку.

Хотя, например, в солонке может оказаться сахар вместо соли — так на самом деле случается во второразрядных кафетериях. Или крышка с отверстиями, через которые высыпается соль, может быть плохо закреплена, и тогда в тарелке ни о чем не подозревающей жертвы окажется столько соли, что ее хватило бы для целой роты солдат. Но если пользоваться солонкой внимательно, тогда основные проблемы будут связаны с недостатками дизайна. Основные претензии могут быть такими: а) дырочки неудобного размера — из них высыпается или слишком много, или слишком мало соли; b) солонку трудно отличить от перечницы (это случается, если для солонки и перечницы выбран модернистский минималистский дизайн или, напротив, вычурный дизайн в стиле китч: вы, наверное, видели фарфоровые солонки в виде собачек или пожарных гидрантов); с) солонку слишком сложно наполнять.

Разумный план таков. Сначала нужно высыпать немного соли из солонки на тарелку, убедившись в том, что она высыпается нормально и что это действительно соль. Потом проведите для обсуждения достоинств и недостатков данного дизайна солонки фокус-группу. Дайте возможность участникам этой дискуссии испробовать солонку в реальных условиях и сравнить ее с другими типами солонок. Попросите прокомментировать проблемы, речь о которых шла выше.

Для тостера важно учесть, насколько точно он выдерживает температурный режим и прожариваются ли тосты так, как вам хочется, можно ли в нем готовить замороженные вафли или булочки, насколько легко очищать тостер от крошек, насколько эффективно он использует электроэнергию, сколько места занимает, насколько привлекателен его дизайн, насколько он безопасен (что произойдет, если пролить в него кофе или если кто-то попытается доставать из него тосты металлической вилкой?).

Для тестирования чайника нужно использовать такие критерии. Сколько чашек воды можно в нем вскипятить? Сколько времени уходит на то, чтобы вскипятить стандартное количество воды (допустим, 1,5 литра)? Когда чайник начинает свистеть (речь идет о чайнике со свистком, который греется на плите), вода уже закипела или вот-вот закипит? Легко ли услышать свист закипевшего чайника, если вы находитесь в другой комнате?

Проблема номер один для лифтов — это, вероятно, безопасность (поэтому вам нужно провести тщательную проверку всех параметров безопасности). Если с этим все в порядке, то следующий вопрос — скорость, причем это не столько проблема механической конструкции, сколько проблема организации «пассажиропотоков» в здании. Вы должны продемонстрировать, что вы ясно понимаете: в каждом здании своя специфика, и удовлетворенность людей работой лифта будет зависеть от того, насколько хорошо он справляется с «пассажиропотоками» в данном здании. Вам стоит учесть, сколько времени в среднем проходит с того момента, как нажата кнопка лифта, до того, как лифт прибудет, и сколько времени уходит на то, чтобы попасть на разные этажи в разное время дня.

Как вы отыщете нужную вам книгу в большой библиотеке?

Допустим, там нет системы каталогизации и библиотекаря, который мог бы вам помочь. Предположим также, что книги размещены в случайном порядке, во всяком случае вам неизвестно ничего другого. В этом случае все, что вы можете сделать, это методично обыскивать полку за полкой — это лучше, чем просто беспорядочно метаться по библиотеке без всякого плана. Скорее всего вам придется осмотреть половину библиотеки, прежде чем вы отыщете нужную книгу.

И все же есть все основания предположить, что книги в библиотеке размещены в каком-то порядке. Любая библиотека, достаточно большая для того, чтобы в ней было нелегко отыскать нужную книгу, размещает книги на полках, следуя какой-то системе, аналогично тому, как нельзя построить достаточно большое здание без архитектурного проекта. Основная ваша проблема не в том, что книги расставлены на полках бессистемно, а в том, что вы не знаете, по какой именно системе они расставлены.

В большинстве библиотек книги размещают в соответствии с их номерами в каталоге. Две наиболее популярные системы книжных каталогов в США — десятичная система Дьюи и система Библиотеки Конгресса США — отличаются друг от друга, и их нельзя считать универсальными. В библиотеках раритетных книг их обычно размещают в соответствии с датой первой публикации. Есть и просто странные системы. Например, в библиотеке института Warburg книги на разные темы специально перемешаны на полках, чтобы вызывать неожиданные ассоциации, помогающие развитию междисциплинарных исследований. Основатель этого института Эйби Варбург придумал и внедрил эту систему еще до того, как был помещен в сумасшедший дом для лечения.

Лучший способ решения — сначала попытаться разобраться в системе размещения книг, а потом использовать ее для поиска нужной книги. Вам необходима карта библиотеки. Поскольку вам ее не вручили, нужно сделать ее самому. Хороший прием — отмечать расположение полок на клетчатом листе бумаги, осматривая их с определенным шагом. Вы можете, например, просматривать несколько книг на верхней левой полке каждой двадцатой секции (или шкафа) в каждом втором ряду. Ваша цель — составить план, но при этом не увязнуть в деталях.

Каждый раз, просматривая книги, обращайте внимание не только на их тематику и названия, но и на систему размещения на полке. Можно ли утверждать, что книги, близкие по тематике, стоят рядом? (Скорее всего так и есть, и тогда это очень важная и полезная информация.) Или они расставлены в случайном порядке? (Будем надеяться, что это не так, но нужно проверить.) Расставлены ли книги по алфавиту (по авторам, по названию, по тематике) или это полка для книг крупного формата, которые стоят здесь, так как не поместились на обычных полках? Везде ли, где вы проверили, система размещения книг одинакова или она варьируется?

Допустим, книга, которую вы ищете, это The Seattle Junior League Microwave Cookbook («Сборник кулинарных рецептов для микроволновой печки для начинающих кулинаров Сиэтла»). Если вы наткнетесь на полку, где размещаются кулинарные книги, — вам повезло. Нужная вам книга где-то поблизости. Если в библиотеке не очень много кулинарных книг, вы можете не составлять план и просто просмотреть полки с кулинарными книгами, но если таких книг очень много, вам все равно понадобится план. Имеет смысл изменить план выборочных поисков, используя более крупный (то есть подробный) масштаб и поместив в центр плана уже обнаруженную вами полку книг с кулинарными рецептами. Возможно, вы обнаружите разделы с книгами рецептов американской кухни, раздел с кулинарными рецептами для микроволновок, раздел с кулинарными рецептами северо-запада тихоокеанского побережья США или рецептами для благотворительных кухонь для бездомных.

Что если во время первого этапа поисков вы не обнаружите никаких кулинарных книг и вообще никаких книг, имеющих отношение к приготовлению пищи? В этом случае вам нужно еще раз обыскать библиотеку, но уже более подробно: проверять не каждый двадцатый стеллаж или шкаф, а каждый пятый. Если понадобится, вам нужно будет снова и снова исследовать библиотеку, все более и более подробно, пока вы не найдете какие-то книги, имеющие отношение к нужной вам.

Неудача в поиске «близких по тематике» книг — это не единственная возможная проблема. В больших библиотеках популярные кулинарные книги могут храниться в отделе справочной литературы, недавно опубликованные — в отделе новых поступлений, старые — в отделе манускриптов и рукописей, книги на иностранных языках — в отделе книг на данном языке, кулинарные книги, напечатанные шрифтом Брайля, — вместе с другими книгами для незрячих и, наконец, основная масса кулинарных книг — в специализированном разделе книг по кулинарии. Эти отделы библиотеки обычно не располагаются рядом друг с другом. Это значит, что, даже если вы нашли один из разделов с книгами по кулинарии, нет гарантии, что нужная вам книга именно там.

Итак, вот основной план: вы проводите систематический выборочный поиск, все более подробный, пока вам не попадутся книги, близкие по тематике к книге, которую вы пытаетесь найти (это значит, что на полке будут в основном книги по этой теме). Теперь ваши поиски должны стать более фокусированными. Систематически и все более подробно исследуйте соседние полки, пока не найдете нужную книгу или не поймете, что ее здесь нет. Во втором случае нужно перейти в другой «перспективный» регион библиотеки и продолжить поиски; если других «перспективных» регионов нет, возобновите вашу рекогносцировку снова во всей библиотеке, пока не найдется «перспективный регион».

Вот такой примерно ответ ожидают интервьюеры Microsoft. Более краткий ответ предлагается на веб-сайте acetheinterview.com: «Я выйду из библиотеки, отыщу человека, придумавшего этот вопрос, и дам ему оплеуху».[139]

Допустим, вы поступили работать в правительственное агентство по сбору налогов (IRS). Ваше первое задание — проверить, честно ли платит налоги фирма, предоставляющая услуги нянь для детей. Как вы выполните это задание?

Есть два основных способа, которые используются в мире бизнеса для ухода от налогов: преувеличение расходов и преуменьшение доходов. В налоговой декларации фирмы она заявляет о своих доходах и расходах. Вам нужно найти какой-то способ проверить эту информацию, воспользовавшись независимыми источниками, и, если она окажется несоответствующей действительности, организовать более тщательную дополнительную проверку.

Нет проблем с оценкой расходов фирмы. IRS обычно достаточно хорошо представляет, сколько фирма определенного размера в той или иной отрасли бизнеса может потратить на канцелярские принадлежности и оплату телефонных счетов, на аренду офиса и зарплаты работников, на рекламу и свой сайт в Интернете. Если есть какие-то сомнения, их легко разрешить во время визита в фирму — сразу станет ясно, верна ли информация о количестве сотрудников фирмы и арендной плате. Труднее проверить информацию о доходах. Фирма по предоставлению услуг нянь находит желающих получить такую работу и направляет их в семьи, получая плату за услуги нянь от родителей детей, за которыми няни присматривают, и выплачивая няням зарплату. После этого всю ответственность за уплату налогов несут семьи-наниматели и сами няни. Семьи обязаны заполнить форму W-2 и уплатить налог в фонд страхования по безработице.

Это дает один из возможных способов проверить работу фирмы, предоставляющую услуги нянь, при помощи данных, уже имеющихся в распоряжении IRS. Для этого, пользуясь налоговыми формами W-2 и 1040, можно составить список нянь, работающих в данном районе. Сравнив эти данные за прошлый год по тем же формам W-2 и 1040, IRS может определить, сколько новых нянь появилось за прошедший год.

Разумно предположить, что большинство из них работает через агентства. Конечно, есть опытные няни с хорошими рекомендациями, которые переходят из семьи в семью, которых рекомендуют своим знакомым родители подросших детей, кроме того, заботу по присмотру за детьми берут на себя бабушки и другие родственники, которым иногда платят за это, иногда нет, но в любом случае сведения об этом не поступают в IRS. Но большинство родителей, которым нужна няня, а друзья и знакомые не могут им никого посоветовать, скорее всего обратятся в агентства. Никто не захочет доверять своего ребенка незнакомцу, который не прошел никакой проверки.

Таким образом, почти каждая начинающая няня получает зарплату в какой-то фирме, предоставляющей услуги нянь. Если та фирма, деятельность которой расследуется, единственная в данном регионе, она получит почти весь доход. Если в данном регионе работает несколько подобных агентств, вам нужно будет рассчитать, как доход от работы новых нянь распределяется между этими фирмами (но имейте в виду, что вам нужно будет получить и проанализировать данные обо всех этих фирмах).

Таким образом, можно провести независимую проверку доходов фирмы, предоставляющей услуги нянь, если предполагается, что и семьи и няни честно предоставляют информацию в налоговое ведомство. А если нет?

Ну, не забывайте, что это как раз обязанность IRS — проверять, насколько честны люди. Вы можете воспользоваться для сравнения известными данными о том, какая доля людей честно платит налоги. Например, если известно, что примерно 90 процентов нянь честно сообщают о своих заработках и 10 процентов скрывают их, вы можете соответствующим образом скорректировать ваши оценки в сторону повышения. Вы анализируете поведение только одного агентства и большого количества нянь — это значит, что по закону больших чисел доля нянь, честно платящих налоги в регионе, будет близка к этому среднему проценту.

У вас восемь бильярдных шаров…

Весы, которыми вы должны воспользоваться, такие же, как весы в руке у богини правосудия Фемиды. Они могут только показать, какая из двух чаш весов тяжелее, но вы не сможете узнать, насколько.

Очевидное решение не подходит. Если вы положите на каждую чашку весов по четыре шара, то вы узнаете, в какой из четверок дефектный тяжелый шар. Потом, если вы еще раз поделите эту четверку пополам и положите на каждую чашку по два шара, вы найдете «двойку», в которой есть дефектный шар. Но в этом случае вы уже использовали два разрешенных взвешивания, а дефектный шар еще не найден. Вы не сможете определить, какой из двух «подозреваемых» шаров тяжелее.

Решение возможно, если вы используете еще одну полезную особенность весов: если вес двух групп шаров одинаков, чаши весов уравновесятся. Если это произойдет, вы можете сделать вывод, что среди взвешенных шаров нет дефектного.

Во время первого взвешивания положите по три любых шара на каждую чашку весов. Возможно два разных исхода.

Первый — чаши могут уравновеситься. В этом случае дефектный шар — это один из тех двух шаров, которые вы не взвешивали. Поэтому во время второго и последнего взвешивания вы кладете на весы эти два шара — более тяжелый и есть дефектный.

Другой возможный исход первого взвешивания: одна из двух чашек весов оказывается тяжелее. Дефектный шар должен быть на этой перевесившей чашке весов. Во втором взвешивании вы сравниваете любые два шара из этой тройки. Если один из них оказывается тяжелее, чем другой, — это и есть дефектный шар. Если шары одинакового веса — дефектный шар тот, который вы не взвешивали.

Эта головоломка хорошо известна во всем мире. Она была, например, опубликована в 1956 году в книге Бориса Кордемского «Математическая смекалка», которая была бестселлером в Советском Союзе времен «холодной войны».[140]

Если у вас пять баночек с таблетками…

В данном случае у вас весы, которые показывают вес (а не весы без гирь, о которых шла речь в задаче о биллиардных шарах).

В реальной жизненной ситуации вы, наверное, просто взвешивали бы по одной таблетке из каждой баночки, пока не обнаружили бы ту, которая весит 9 граммов, но вы не можете так поступить, поскольку разрешается только одно взвешивание. Шансов на то, что вам в первом же взвешивании попадется дефектная таблетка, один из пяти.

Это значит, что вам нужно одновременно взвешивать таблетки не из одной баночки, а из нескольких. Рассмотрим простейший случай: вы взвешиваете пять таблеток, по одной из каждой баночки. Тогда итоговый вес обязательно окажется 10+ 10 + 10+ 10 + 9 = 49 граммов. Проблема в том, что это можно узнать и без всякого взвешивания. Это никак не поможет вам узнать, из какой баночки вы взяли дефектную 9-граммовую таблетку.

Вам нужно придумать такую ситуацию, в которой вес таблеток был бы информативным. Одно из решений—пронумеровать баночки №1, №2, №3, №4, №5. Потом вы кладете на весы одну таблетку из баночки №1, две — из №2, три из №3, четыре из №4 и пять из №5. Вы взвешиваете одновременно все эти таблетки. Если бы все таблетки были нормального веса, то результат был бы 10 + 20 + 30 + 40 + 50 = 150 граммов. На самом деле вес будет меньше, причем на количество граммов, которое соответствует номеру баночки с испорченными таблетками. Например, если общий вес будет 146 граммов (на 4 грамма меньше), это значит, что более легкие дефектные таблетки — в баночке №4.

Альтернативное решение позволяет определить дефектную бутылку, взвесив меньше таблеток: 1 + 2 + 3 + 4 таблеток из первых четырех баночек. Тогда если вес окажется меньше 100 граммов, то количество граммов, которого не хватает до 100, укажет вам номер дефектной баночки. Если же вес будет ровно 100 граммов, это означает, что дефектные таблетки в пятой баночке.

После того, как вы найдете правильный ответ, вы можете спросить интервьюера о том, для кого предназначаются эти таблетки. Хороший ответ на этот вопрос — «для лошади». 10-граммовая таблетка весит в тридцать раз больше, чем обычная (325 миллиграммов) таблетка аспирина.

Эта головоломка (правда, речь шла о взвешивании монет) упоминалась Мартином Гарднером в его колонке в журнале Scientific American в середине 1950-х. Гарднер описывал ее как «новую и элегантную вариацию» задач о взвешивании, «популярных в последние годы».[141]

Три муравья находятся в трех углах равностороннего треугольника…

Есть два способа движения, при котором муравьи не встретятся друг с другом: они все должны двигаться по часовой стрелке или все против часовой стрелки. В противном случае встречи им не избежать.

Выберите одного муравья и назовите его, например, Биллом. После того, как Билл решил, в какую сторону двигаться (по часовой стрелке или против часовой стрелки), другие муравьи должны двигаться в том же направлении, чтобы не столкнуться. Поскольку муравьи принимают решение случайным образом, шансы на то, что второй муравей направится в ту же сторону, что и Билл, — один из двух, аналогично и для третьего муравья эта вероятность такая же. Это значит, что вероятность избежать столкновения — один из четырех.

Четыре собаки находятся в разных углах большого квадрата…

Чтобы упростить решение задачи, предположим, что длина стороны квадрата 1 миля, а собаки — это гончие, выведенные генетиками, которые бегут со скоростью ровно одна миля в минуту. Представьте себе, что вы блоха, которая едет на спине собаки номер 1. У вас есть крошечный радар, который позволяет вам точно измерить скорость движения других объектов относительно вашей системы отсчета (ею служит в данном случае собака номер 1, в шерсть который вы вцепились пятью вашими лапками, а в шестой вы держите радар). Собака 1 преследует собаку 2, которая преследует собаку 3, которая преследует собаку 4, которая, в свою очередь, преследует собаку 1. В начале погони вы направляете радар на собаку 4 (которая гонится за вами). Радар вам сообщает, что собака 4 приближается к вам со скоростью 1 миля в минуту.

Чуть позже вы снова проверяете показания вашего ручного радара. И что же вы видите теперь? В этот момент все собаки уже пробежали какое-то расстояние и находятся ближе друг к другу и все они немного изменили направление движения, чтобы направляться точно к той собаке, которую они преследуют. Четыре собаки все еще образуют правильный квадрат. Каждая из них по-прежнему преследует свою «собаку-мишень» со скоростью 1 миля в минуту, и каждая «мишень» движется, как и раньше, под прямым углом к преследователю. Поскольку все мишени движутся под прямым углом к направлению движения преследователей, те догоняют их на полной скорости. Это означает, что ваш радар по-прежнему покажет, что собака 4 приближается к вам со скоростью 1 миля в минуту.

Такими же будут показания радара в течение всей погони: собака 4 приближается к вам на скорости 1 миля в минуту. Все эти рассуждения о блохах и радарах — всего лишь красочный способ проиллюстрировать то, о чем говорится в условии задачи: собаки догоняют свои «мишени» с постоянной скоростью.

Не играет никакой роли, что ваша система отсчета (то есть собака) сама движется относительно других собак. Эта система отсчета не хуже любой другой (если интервьюеры станут к вам приставать по этому поводу, отвечайте им, что так сказал Эйнштейн). Единственное, что играет роль, — собака 4 приближается к вам с постоянной скоростью. Поскольку в начале погони собака 4 находилась от вас на расстоянии одной мили и приближалась к вам с постоянной скоростью 1 миля в минуту, она непременно столкнется с вами через одну минуту. Блохи-наездники на других собаках, несомненно, придут к такому же выводу. Все собаки столкнутся друг с другом через минуту после старта.

Где это произойдет? Собаки движутся по абсолютно симметричным траекториям. Было бы странно, если бы они при этом отклонились на «две трамвайные остановки» к востоку или западу. Нет никакой силы, которая бы подталкивала их к востоку или западу. Что бы ни происходило, симметрия исходной ситуации должна сохраниться. Если уж собакам суждено догнать друг друга — это произойдет точно в середине квадрата.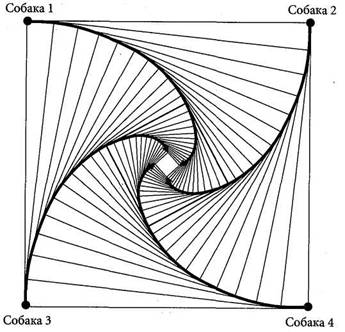

Если посмотреть сверху, то траектория движения каждой из собак окажется изящной спиралью, но вам не нужно этого знать, чтобы решить задачу. Вам также не нужно использовать, вопреки тому, что предлагают многие люди, интегральное исчисление. Этот вопрос как раз и проверяет, не помешают ли вам школьные знания высшей математики найти более простое решение.

Эту задачу также в 1950-х годах упоминал Мартин Гарднер.[142]

Поезд отправляется из Лос-Анджелеса в Нью-Йорк с постоянной скоростью…

Птица всегда останется самым быстрым объектом в этой головоломке. Ничего из того, что делает птица, никак не может повлиять на то, что происходит с поездами.

Назовем поезда Восточным (тот, что идет на восток) и Западным (тот, что идет на запад). Поскольку птица быстрее, чем Восточный поезд, она долетит до Западного поезда раньше, чем он встретится с Восточным, то есть до крушения.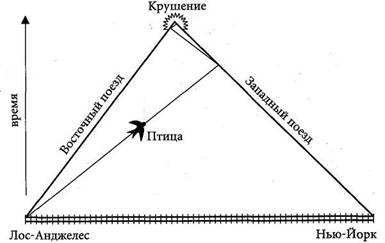

В тот самый миг, когда птица долетит до Западного поезда, она поворачивает и летит в обратную сторону. Теперь она уже летит впереди Западного поезда на запад навстречу Восточному. И снова птица первая встретится со встречным поездом. Она снова поворачивает обратно, и начинается новый цикл. Единственная разница в том, что с каждым новым циклом поезда оказываются все ближе и ближе друг к другу. Неважно, насколько близко, потому что птица каждый раз успевает улететь в обратную сторону еще до того, как произойдет столкновение. Это значит, что птица снует туда-сюда бесчисленное множество раз.

Во всяком случае теоретически. За мгновение до столкновения птица окажется зажатой между поездами, которые ее раздавят, но вы можете не обращать внимания на подобные кровавые подробности.

Труднее игнорировать бесконечные ряды. Большинство людей, которых интервьюируют в Microsoft, когда-то изучали их, но многие уже позабыли ко времени интервью в Редмонде.

Вообще-то можно не беспокоиться о бесконечных рядах. Два поезда сближаются с относительной скоростью 35 миль в час (15 + 20 миль в час). Допустим, расстояние между Нью-Йорком и Лос-Анджелесом — 3500 миль. Тогда столкновение поездов произойдет через 3500/35, или 100 часов.

Все это время птица будет в полете, летая между поездами с постоянной скоростью 25 миль в час. Хотя направление полета и меняется, она тем не менее постоянно летит именно с этой скоростью. Таким образом, летая со скоростью 25 миль в час в течение ста часов, птица пролетит 25 х 100 = 2500 миль. Или, если D — это реальное расстояние между Лос-Анджелесом и Нью-Йорком, то столкновение между поездами произойдет через D/35 часов, а птица за это время пролетит 25D / 35, или 5D / 7 миль.

Рассказывают, что кто-то задал один из вариантов этой задачи математику Джону фон Нейману (1903-1957). Тот так быстро дал ответ, что его знакомый сказал: «Ну, ты, наверное, знал, в чем здесь трюк».

«Какой трюк? — спросил Фон Нейман. — Я просто вычислил сумму бесконечного ряда».

У вас 26 констант…

Вы читаете английские тексты слева направо, поэтому, допустим, что вы попали в эту ловушку и начали анализировать выражение слева. Что такое константа X?

X — это двадцать четвертая буква английского алфавита, равная 24, возведенным в степень, значение которой равно значению предыдущей константы W. Поскольку W — это двадцать три в степени U, которая 22 в степени Т, которое 21 в степени… X

Все это значит, что X — это 24, возведенные в степень 23 в степени 22 в степени 21… и так далее, до 3 в степени 2 в степени 1. То есть это 23-ступенчатые экспоненты.

X — это очень большое число.

Поисковый интернет-портал Google (произносится Гугл) получил свое название от числа, название которого, правда, пишется чуть иначе — googol (гугол), значение которого можно записать как единицу со ста нулями. Есть еще большее число, названное googolplex (гуголплекс)—это единица, за которой следует гугол нулей. Ни гугол, ни гуголплекс не имеют никакого практического применения за исключением иллюстрации того факта, что существуют абсурдные огромные числа. В наблюдаемой вселенной нет никаких объектов, количество которых составляло бы гугол. А гуголплекс — это такое огромное число, что его даже не записать. Поскольку количество нулей в этом числе — гугол, а даже количество атомов или кварков во вселенной меньше, вам никогда не написать это число на бумаге, сколько бы у вас ни было бумаги и каким бы мелким почерком вы ни писали.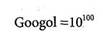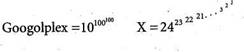

Но даже гуголплекс — это маленькое число, если сравнить его с числом X из головоломки Microsoft. Корпорация Intel еще не изготовила достаточно микропроцессоров, чтобы рассчитать значение X. Даже если закон Мура будет выполняться до конца времен и каждые пять лет будут появляться новые Супер-Пентиумы и вы заполните всю вселенную этими процессорами, вы все равно не сможете рассчитать невообразимо огромное значение X.

Тот факт, что интервьюер просит вас рассчитать точное количественное значение выражения, в котором таких X множество, должно подсказать вам, что здесь есть какой-то трюк.

Правильный ответ — ноль. Среди 26 сомножителей должен быть один со значением (X — X) — а это, конечно, ноль. Неважно, чему равны все остальные сомножители — что бы вы ни умножили на ноль, результатом все равно будет ноль.

У таких вопросов с подвохом может быть разная форма. Этот похож на детские картинки-загадки, на которых нужно отыскать спрятавшихся мальчиков или кошку. Нет общего правила поиска трюка — подобно кошке на загадочной картинке, трюк может быть спрятан где угодно. То, насколько быстро вы обнаружите трюк, зависит от того, на что вы обратите внимание в первую очередь, во вторую и третью. Ключевой множитель (X — X), естественно, «спрятан» там, где интервьюеры Microsoft ставят многоточие в выражении, которое нужно вычислить по условиям задачи.

Резонно проверить, умеет ли кандидат на работу сначала оценить всю ситуацию в целом, прежде чем тратить время и энергию на какое-то занятие, которое может оказаться бессмысленным. Но для многих людей «ситуация в целом» в первую очередь характеризуется тем, что им нужно пройти трудное интервью, во время которого любые сомнения и колебания могут снизить их шансы на успех. Даже если в нормальной ситуации эти люди склонны сначала проанализировать проблему, а уже потом заниматься вычислениями, и даже если они подозревают, что задача может быть с подвохом, в стрессовой ситуации они начинают заниматься алгебраическими вычислениями, то есть привычно двигаются «слева направо». Они могут идти по этому неверному пути некоторое время и только потом найти простое решение.

Разработайте систему счисления с основанием минус 2.

Эта глупая просьба долго использовалась в интервью, проводившихся в компании Microsoft. На самом деле нет никакого «минус двоичного» счисления. Это все равно, что попросить кого-нибудь написать несколько предложений на языке Клингонов — фантастической инопланетной расы из сериала Star Trek.

Тем не менее можно изобрести логичную и последовательную систему счисления с основанием минус 2. Это как раз то, что от вас ожидается.

Мы пользуемся системой счисления с основанием 10. Это значит, что, когда мы записываем числа, мы представляем их как степени числа 10. Например, 176 — это 1 х 10 + 7 х 10 + 6 х 100. (Существует договоренность, что любое число в степени 0 равно 1.) Еще одна важная особенность десятичной системы счисления — это то, что в ней используется десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9).

Компьютеры используют систему счисления с основанием 2, или двоичную. В ней используются только две цифры (0 и 1). В многозначном числе (таком, как 10 010) каждый знак или позиция обозначает последовательные степени числа два — 1, 2, 4, 8, 16, 32… Двоичное число, например 10 010, означает 1 х 2 в четвертой степени + 0 х 2 + 0 х 2 + 1 х 2 + 0 х 2 в нулевой. В обычной, десятичной системе счисления оно равно 18.

В общем, система счисления с любым основанием похожа на систему строительных блоков разных размеров. В десятичной системе размеры этих блоков 1, 10, 100, 1000 и т.д. В двоичной системе размеры блоков — 1, 2, 4, 8, 16 и т.д. Используя комбинации этих «блоков», можно получить любое нужное число.

Итак, какими будут обозначения в системе счисления с основанием минус 2?

Очевидно, что в этой системе счисления числа должны выражаться как суммы степеней числа 2. Последовательность степеней числа —2: -2, 4, -8, 16, -32…

Она отличается тем, что нечетные степени оказываются отрицательными (-2 х —2 = +4, но —2 х —2 х —2 = —8). Таким образом, вам нужно выразить числа как сумму этих положительных и отрицательных степеней.

Вы можете усомниться, можно ли этого добиться для любого числа? Да, можно. Вы можете таким способом записать любые положительные и отрицательные числа (при этом вам не понадобятся знаки плюс и минус, которыми вы обозначаете положительное это число или отрицательное в десятичной системе). В целом для того, чтобы отобразить число в системе счисления с основанием минус 2, нужно больше разрядов, чем в обычной двоичной системе.

Перед тем, как мы начнем считать, нужно решить еще одну проблему. Какие цифры мы станем использовать в минус двоичной системе? 2? 0 и 1? 0 и -1? Или нечто совершенно другое?

В системах с нормальным основанием количество цифр равно основанию. В десятичной системе десять цифр, в двоичной — только две цифры.

Если бы вы стали буквально следовать этому правилу, то пришли бы к заключению, что в минус-двоичной системе должно быть минус две цифры — это даже меньше, чем вообще ни одной цифры.

Правила создаются для того, чтобы их нарушать, и все же есть изящные нарушения правил и неряшливые нарушения. Вам нужно сохранить «дух» позиционной системы счисления и перенести его на «инопланетную» почву отрицательных чисел. Правило, что количество цифр равно основанию, неприменимо для систем счисления с негативным основанием.

Наиболее очевидное решение использовать цифры 0 и 1. Это те же цифры, которые используются в обычной двоичной системе счисления. Альтернативное решение, возможно, более соответствующее духу минус двоичной системы счисления, — использовать цифры 0 и —1, причем последняя цифра должна восприниматься как единый символ. Хотя это несколько трудно и тяжеловесно. Остановимся на более простом варианте с цифрами 0 и 1.

Единицу можно просто записать как 1 (это значит 1 х (-2) в нулевой степени).

С двойкой сложнее. Вторая позиция, считая справа налево, — это —2. Это значит, что 10 (в минус двоичной системе) будет 1 х (-2) в первой + 0 х (-2) в нулевой = —2 + 0, или —2.

Попробуйте 111. Это 1 х (-2) в квадрате + 1 х (-2) в первой + 1 х (-2) в нулевой = 4 + (-2) + 1 = 3. Теперь замените единицу на ноль в первой справа позиции: 110 = 4 + (-2) + 0 = 2. Итак, вот что мы должны написать в минус двоичной системе для того, чтобы получилась двойка, — 110.

И мы только что выяснили, что тройка в минус двоичной системе — 111.

С четверкой все просто. Третья позиция — это 4, как и в обычной двоичной системе. Четыре записывается как 100.

Если вы поставите единицу в крайней справа позиции, то получится пятерка в минус двоичной системе, или 101.

Для того чтобы получилось шесть, не стоит ставить 1 во второй или четвертой позициях справа, так это дает негативные числа (соответственно —2 и —8). Вам нужно перепрыгнуть на пятую позицию, единица в которой обозначает +16. Таким образом, 10 000 — это 16. Это слишком много, но 11 000 — это 16 + (-8) = 8. Отнимите от этого числа двойку — для этого нужно поставить 1 во второй справа позиции (11 010), и вы запишете шестерку в минус двоичной системе.

Семерка получается, если добавить 1 в крайней правой позиции

(11011).

Мы уже раньше узнали, что 11 000 — это восемь.

Добавьте единицу в первой справа позиции — получите девять (11001).

С десяткой придется повозиться. Начните с восьмерки (11 000). Добавьте к этому числу четыре, поставив 1 в третьей позиции (11 100). Теперь вычтите два, поставив 1 во второй позиции (11 110). Это и есть десять.

Итак, первые десять чисел в позиционной системе счисления с основанием минус 2 — это: 1, 110, 111, 100, 101, 11010, 11011, 11000, 11001 и 11110.

У вас два сосуда и 100 шариков…

На первый взгляд кажется, что изменить вероятность в ту или иную сторону невозможно. Количество красных и синих шариков абсолютно одинаково. Вам нужно все их использовать — нельзя «потерять» несколько синих шариков. Шарики достают абсолютно случайным образом. Разве шансы достать красный шарик не должны быть 50 на 50?

Так и будет, если вы положите 25 шариков каждого цвета в оба сосуда. Более того, вероятность будет 50 на 50, когда в каждом из сосудов по пятьдесят шариков независимо от того, в какой пропорции в каждом из них перемешаны цвета. Положите все красные шарики в сосуд А, а все синие — в сосуд В. И в том случае вероятность вытащить красный шарик в точности 50%, потому что такова вероятность выбора сосуда А (а любой случайно выбранный из него шарик, как мы знаем, окажется красным).

Вот что может подсказать ответ на задачу. Вам не нужно класть все 50 красных шариков в сосуд А. Достаточно положить туда всего один красный шарик: ведь и в этом случае вероятность того, что будет выбран сосуд А, остается 50 процентов. Тогда и в этом случае из него случайным образом будет «выбран» только красный шарик — учитывая, что выбирать-то там нечего.

Таким образом, уже только за счет сосуда А вероятность выбора красного шарика составит 50 процентов. Но у вас еще осталось 49 красных шариков, которые вы должны положить в сосуд вместе с 50 синими. В этом случае, если будет выбран сосуд В, шансы выбрать красный шарик из этого сосуда также будут почти 50 на 50 (в действительности эта вероятность равна 49 из 99). Таким образом, вероятность выбора красного шарика в целом (когда шарик случайным образом берется из одного из двух сосудов) будет чуть меньше 75 процентов (50% + 1/2 от 49/99, а если сосчитать точно — 74,74%).

Вот такой трюк используется при определении избирательных округов.

У вас есть два ведра емкостью 3 литра и 5 литров и неограниченный запас воды. Как можно отмерить точно 4 литра воды?

Давайте подумаем о том, какое количество воды вы можете отмерить. Опустите 3-литровое ведро в колодец с неисчерпаемым запасом воды и вытащите его с водой: вот вам 3 литра воды. Проделайте то же самое с другим ведром — вот и еще 5 литров.

Для того чтобы отмерить любое другое количество, вам нужно разрешить неопределенность в формулировке условия задачи. Какие действия разрешается совершать, чтобы «точно отмерять нужное количество воды?»

Если бы у вас был «не глаз, а алмаз», вы могли бы на глазок отлить точно один 1 воды из 5-литрового ведра. Это и было бы решением задачи. Очевидно, так вы поступить не можете — иначе вам бы не задавали эту задачу.

Конечно, вы можете добавлять воду. Если бы вам удалось каким-то образом налить по 2 литра воды в 3-литровое ведро и в 5-литровое, то, перелив содержимое 3-литрового ведра в 5-литровое, вы бы получили ровно 4 литра воды.

Но, похоже, что эта операция ничего вам не дает. Вам даже никак не получить 3 + 3 = 6 литров воды, потому что в 5-литровом ведре 6 литров воды не поместится. Вы можете подумать о том, чтобы переливать отмеренное количество воды в ванну, пустой плавательный бассейн, пересохшее озеро — да куда угодно. Интервьюер не разрешит вам делать это. Вы можете представить, что находитесь на планете, которая вся покрыта океаном, и ваши два ведра — это единственные сосуды в этом мире.

Раз уж сложение не помогает решить эту задачу, вы можете попробовать использовать чуть более сложное действие, а именно вычитание. Налейте 5 литров воды в большее ведро, а затем аккуратно переливайте воду в 3-литровое ведро, пока оно не заполнится. А теперь стоп! Если вы ничего не пролили, то теперь у вас в 5-литровом ведре ровно 2 литра воды.

Если вы их оставите в 5-литровом ведре, то никогда не решите эту задачу. Единственный способ продвинуться в ее решении — опорожнить 3-литровое ведро и перелить два литра из 5-литрового ведра в 3-литровое.

Теперь вам нужно наполнить до краев 5-литровое ведро, а затем аккуратно отливать из него воду в 3-литровое ведро, пока оно не заполнится до краев. Таким способом вы отольете из 5-литрового ведра 1 литр воды, а это значит, что в нем останется 4 литра воды.

Альтернативное решение (для него потребуется переливать воду на один раз больше) — это наполнить 3-литровое ведро водой и перелить из него воду в 5-литровое ведро. Потом проделать это еще один раз и снова перелить воду в 5-литровое ведро, пока оно не заполнится до краев (тогда в 3-литровом ведре останется 1 литр воды). Теперь вылейте воду из 5-литрового ведра. Перелейте 1 литр воды в пустое 5-литровое ведро. Снова наполните 3-литровое ведро и перелейте из него воду в 5-литровое ведро, после чего в нем окажется 4 литра воды.

У.У. Раус Болл упоминает эту головоломку в своем сборнике Mathematical Recreations and Essays («Математические досуги и эссе», 1892 год), популярном в викторианскую эпоху. Болл считал, что эту головоломку придумали в средние века.

Хотя Льюис Терман использовал более простую версию этой задачи в своем первом тесте IQ, он сообщал, что две трети «обычных взрослых людей» не успевали решить эту задачу за отведенные на это пять минут. «Если читателю покажется, что для решения этой задачи от него требуется слишком много изобретательности, — писал Терман, — стоит напомнить читателю, что в истории человечества важные изобретения не рождались неожиданно, подобно Минерве[*], но делались постепенно, шаг за шагом».[143]

Минерва-Шминерва — версия задачи, использованная Терманом, действительно легкая. Это может отражать долговременную тенденцию увеличения «среднего» балла IQ (которую можно отметить, если вы используете для тестирования интеллекта тот же набор вопросов, что использовался в прошлом). В отличие от ожиданий Термана, среда оказывает существенное влияние на балл IQ.

Более трудная версия этой задачи, применявшаяся Microsoft, была использована в фильме Die Hard with a Vengeance («Крепкий орешек», 1995 год). В этом фильме коварный преступник так настроил бомбу, что она должна была взорваться, если бы Брюс Уиллис и Сэмюель Л. Джексон не решили бы эту задачу. В их распоряжении был фонтан в парке и два пластмассовых ведра указанных размеров. Отмеренную воду нужно было поставить на весы. Они не могли гадать и действовать приблизительно, потому что бомба взорвалась бы даже если бы они ошиблись всего на одну унцию (28,3 грамма). Они не могли и просто уйти, потому что у бомбы был «детектор близости цели». Уиллис и Джексон смогли найти решение, да еще и дружески переругивались при этом («Я тебе не нравлюсь, потому что я белый!» / «Ты мне не нравишься, потому что я из-за тебя могу взлететь на воздух!»).

Один из ваших работников настаивает на том, чтобы ему платили золотом каждый день…

Вам нужен один кусок золота, чтобы заплатить вашему работнику за первый день. Очевидный способ — отрезать один кусок от конца золотого слитка. Менее очевидный способ: отрезать этот кусок в середине слитка, использовав для этого оба разрешенных вам разреза. Попробуйте сначала очевидный план (оставив за собой право пересмотреть свое решение). Вы отрезаете один кусок от конца бруска и отдаете его работнику.

Это оставляет вам слиток, состоящий еще из шести кусков, и один-разрез.

На второй день вы можете отрезать еще один кусок на конце слитка, но тогда у вас останется слиток из пяти кусков, а отрезать от него уже больше ничего нельзя. Вам нечем будет платить работнику на третий день.

Альтернативное решение — отрезать сегмент, состоящий из двух кусков. Тогда в конце второго дня вы можете отдать его работнику и получить от него назад один кусок как сдачу (при этом вы должны надеяться на то, что работник этот кусок еще не потратил).

Это оставит вас со слитком, состоящим из четырех кусков, одним куском, который вы получили как сдачу, а разрезов больше вы уже делать не можете. На третий день вы отдаете работнику один кусок. На четвертый день вы отдаете ему то, что осталось от слитка, то есть четыре куска, а два меньших он вам возвращает как сдачу. Затем вы аналогичным образом используете их, чтобы заплатить работнику на пятый, шестой и седьмой день.

У вас есть b коробок и n банкнот в один доллар…

Основная идея решения аналогична той, что использовалась в задаче о золотом слитке. Вы используете бинарную систему счисления. Положите в первую коробку 1 доллар, во вторую 2, в третью — 4 и т. д. Любую нужную сумму можно представить как сумму различных степеней числа 2.

Отличие от приятной загадки с золотым бруском заключается в том, что данная головоломка проверяет, как вы «справляетесь с исключениями». Одна из сложностей связана с тем, что не все n оказываются суммой последовательных степеней числа 2. У вас, вероятно, образуется какой-то «остаток» денег после того, как вы разложите по коробкам все возможные для данного n последовательные степени числа 2. Еще одна проблема — вам может не хватить коробок.

Допустим, у вас 100 долларов. У вас будут коробки, в которые вы положите 1, 2, 4, 8,16, 32… доллара, но у вас окажется недостаточно денег для того, чтобы в следующую коробку положить 64 доллара, поскольку вы уже положили в предыдущие коробки 1 + 2 + 4 + 8 + 16 + 32 = 63 доллара. Это значит, что у вас есть остаток в 37 долларов, а это число — нечетное и никак не может быть степенью двойки.

Каким же образом вы сможете получить любую требуемую сумму от 0 долларов до 100? Используя первые шесть коробок, вы можете выплатить любую сумму от 0 до 63 долларов (чтобы выплатить 0 долларов, вы «передаете» ноль коробок!!!).

А что если вам нужно выплатить 64 доллара? Сначала вы отдаете седьмую коробку, в которой 37 долларов. Затем вычитаете 37 долларов из 64 долларов, и остается 27 долларов. Эту сумму вы можете выплатить, используя первые шесть коробок, суммы в которых соответствуют степеням числа 2. В данном конкретном случае вы отдаете коробки, сумма денег в которых равна 37, 16, 8, 2 и 1 доллару. Аналогичный принцип можно использовать для любой суммы в пределах 100 долларов.

Когда интервьюер спрашивает вас об «ограничениях» для b и n, он имеет в виду: «Каким образом вы можете определить, будет ли данный план работать для конкретных значений b и n?». Например, очевидно, что, если у вас есть миллион долларовых банкнот и всего одна коробка, такой план работать не будет. У вас недостаточно коробок для такой суммы. Обратите внимание, что обратная проблема вас не должна беспокоить: если у вас мало долларов и много коробок — все в порядке.

Вам нужно найти общую формулу, которая связывает b и n. Набросайте таблицу, показывающую, какую сумму вы можете выплатить, если у вас есть данное количество коробок.

b — n

1 — до 1 доллара

2 — до 2 + 1 = 3 долларов

3 — до 4 + 2 + 1 = 7 долларов

4 — до 8 + 4 + 2 + 1 = 15 долларов.

Это приемлемый ответ. Он будет выглядеть немного более изящно, если вы добавите по 1 к правой и левой части: n + 1 < 2b . Это, аналогично утверждению, что n должно быть меньше или равно 2b.

Как бы ни отражала эта загадка «цифровой дух нашего времени», она использовалась в той или иной форме еще со времен Ренессанса. Обычно ее называют задачей на взвешивание Баше, потому что она была упомянута в книге Клода Каспара Баше Problemes plaisans et dekctables (фр. «Приятные и восхитительные задачи»), опубликованной в 1612 году.[144] Баше спрашивал, какое минимальное количество гирь необходимо для того, чтобы уравновесить любой вес от 1 до 40 фунтов. Еще более ранняя версия этой задачи, тоже о взвешивании, была опубликована в трактате об измерениях Николо Тартальи в Венеции в 1556 году. Ответ, конечно, — 1, 2, 4, 8, 16 и 32 фунта. Для ренессансных гуманистов необходимость использования степеней числа 2 была гораздо менее очевидной, чем для интервьюеров из Microsoft, привычных к использованию двоичной системы счисления.

У вас баночка, в которой драже трех цветов: красного, зеленого и синего…

Четыре. Если вы достаете только три драже — они могут все оказаться разных цветов. Если вы берете четыре драже — по крайней мере два из них обязательно будут одинакового цвета.

Это вариация Microsoft на тему более старой задачи о том, сколько носков вам нужно достать из ящика комода в темноте, чтобы быть уверенными в том, что у вас будет пара, подходящая по цвету. В компании Bankers Trust, например, спрашивают именно о носках. Если носки могут быть двух цветов, то ответ, очевидно, три.

У вас три корзины с фруктами…

Представьте, что вы взяли какой-то фрукт из корзины с надписью «Яблоки». Какую информацию это вам дает? Только один бит информации, который сообщает вам, яблоко это или апельсин. Допустим, это яблоко. Корзина, из которой вы его только что достали с названием «Яблоки», не может быть на самом деле корзиной, где только яблоки. Если уж вы нашли там яблоко, это значит, что в данной корзине должны быть перемешаны яблоки с апельсинами. Прекрасно. Тогда у нас остаются две корзины. На одной из них надпись «Апельсины», а на другой — «Яблоки и апельсины». В корзине «Апельсины» не может быть апельсинов (потому что все ярлыки с названиями ложные), это не может быть и смесь яблок с апельсинами (мы ведь уже знаем, что это корзина с ярлыком «Яблоки», из которой мы достали яблоко). Таким образом, в корзине с ярлыком «Апельсины» должны быть только яблоки, и тогда в корзине с ярлыком «Яблоки и апельсины», очевидно, одни апельсины.

Можно ли считать, что мы нашли решение? Нет. Мы сделали оптимистичное предположение о том, что достанем яблоко из корзины с названием «Яблоки», Это сразу позволяет прийти к выводу, что в данной корзине смесь апельсинов и яблок. Но вы также могли достать апельсин из корзины с надписью «Яблоки». В данном случае невозможно установить, что в этой корзине с надписью «Яблоки» только апельсины или смесь яблок и апельсинов.

Вам нужно быть уверенным в том, что фрукт, который вы достали из корзины, даст вам понять, что в этой корзине. Единственный способ добиться этого— взять фрукт из корзины, на которой ярлык «Яблоки и апельсины». Поскольку все ярлыки неверные, там должны быть фрукты только одного типа. И, достав фрукт, вы знаете, какого именно.

Если это был апельсин, то в данной корзине только апельсины. Тогда у нас остаются две корзины с названиями «Яблоки» и «Апельсины». В одной из этих корзин действительно яблоки, а в другой — смесь. Снова, поскольку известно, что все ярлыки ложные, яблоки не могут находиться в корзине с названием «Яблоки» — они должны быть в корзине с надписью «Апельсины». Это значит, что смесь яблок и апельсинов находится в корзине с названием «Яблоки». Аналогичные рассуждения позволяют решить задачу, если вы достали из корзины с надписью «Яблоки и апельсины» яблоко.

В деревне, где живет пятьдесят семейных пар, каждый из мужей изменял своей жене…

Начните с ситуации, которая существует в деревне до того, как королева сделала свое заявление. Вы знаете, что каждый мужчина изменял своей жене.

Женщины, которые знают о вопиющих нарушениях супружеской верности, должны по закону убить своих неверных мужей. Почему же они еще этого не сделали?

Все дело в том, что только жена неверного мужа обязана его убить. Каждая из женщин деревни знает об изменах мужей других сорока девяти женщин, но ничего не знает об изменах своего собственного мужа. Этикет исключает сообщение этого неприятного факта каждой из женщин.

Это, конечно, странная ситуация, но она вполне обычна для логических головоломок. Но однажды в деревню приезжает королева и говорит, что по крайней мере один муж неверен своей жене. Каким образом это изменит ситуацию?

Никак. По меньшей мере один??? —должно быть, подумают жены, и каждая при этом будет гадать, кого из известных лично ей сорока девяти неверных мужей имела в виду королева. Заявление королевы не сообщило ничего нового кому бы то ни было в деревне.

Вот на чем попадаются многие кандидаты. Если заявление королевы неинформативно — о чем тут еще говорить? Ни одна женщина из-за этого не станет убивать своего мужа. Ничего не произойдет.

И предположение о том, что «ничего не произойдет», верно до конца того дня, когда королева сделала свое объявление.

Ничего не произойдет и на следующий день, и еще через день.

Давайте сразу перепрыгнем в сорок девятый день. Возьмем, к примеру, одну женщину по имени Эдна. Эдне известно об изменах сорока девяти мужей. Среди них есть и Макс — муж ее подруги Моники. Учитывая то, как быстро распространяются слухи, Эдна знает, что Монике должно быть известно (по меньшей мере) о сорока восьми неверных мужьях. Это те сорок восемь, о которых знает Эдна, минус Макс. Никто не осмелится рассказать Монике о проделках Макса.

Теперь вот в чем трюк. На сорок девятый день Эдна должна прийти к выводу, что Моника должна догадаться, что Макс ей неверен. Моника должна понять это (как рассуждает Эдна), потому что никто не был убит в предыдущие дни.

Если бы в деревне был только один неверный муж, его жена должна была убить его в тот день, когда королева сделала свое объявление (назовем этот день первым). Так как в этом случае все женщины знали бы об этом единственном неверном муже за исключением его жены. Она была бы единственной женщиной, которой бы не было известно о неверном муже. Поэтому объявление королевы было бы для нее как удар грома. Поскольку она не знала ни о каких неверных мужьях, этот «по крайней мере» один неверный муж должен быть ее собственным мужем. Она должна была бы убить его в тот самый день, как предписано законом. Конечно, в том случае, если бы в деревне был всего один неверный муж.

Вместо этого настает утро второго дня — и все мужчины живы. Это информирует всех жителей в деревне о том, что неверных мужей более одного. И это, и безупречность королевы подразумевает, что неверных мужей должно быть по крайней мере два.

И если неверных мужей было бы только два, их жены убили бы их на второй день, а если бы их было три — жены бы убили их на третий день, и т. д. И если бы их было сорок восемь — их сорок восемь жен убили бы их на сорок восьмой день.

Сегодня уже сорок девятый день, и Моника, которая знает о сорока восьми неверных мужьях, должна быть удивлена тому, что в предыдущий день не произошло массового убийства. Единственное возможное объяснение (это все еще размышления Эдны о том, что должна была подумать Моника) — муж Моники как раз и есть сорок девятый герой адюльтера.

Таким образом, Эдна должна прийти к заключению, что всегда безупречно логичная Моника должна убить Макса к полуночи сорок девятого дня. Эдна может прийти к подобному же заключению относительно всех остальных женщин деревни. «Да, — думает Эдна, — на сорок девятый день произойдет кровавая баня».

И вот настал сорок девятый день, и все еще ничего не произошло. Единственное возможное объяснение теперь — это то, что Моника (и все остальные женщины) знали о сорок девятом неверном муже. Это не мог быть Макс. Это мог быть только один мужчина: собственный муж Эдны Эдгар!

Итак, на пятидесятый день Эдна должна прийти к заключению, что ее муж неверен ей. Все остальные женщины сделают о своих мужьях такой же вывод.

Ответ на головоломку — ничего не произойдет в первые сорок девять дней, а на пятидесятый день все пятьдесят жен убьют своих мужей.

Это шедевр среди логических головоломок. Однако нельзя с уверенностью утверждать, что эта задача также хороша как инструмент при отборе кандидатов на работу. Первое известное упоминание об этой головоломке в печати — опубликованная в 1958 году книга физика Джорджа Гамоу и математика Марвина Стерна Puzzle—Math («Математические головоломки»).[145] В их версии речь шла о неверных женах. С тех пор эта головоломка широко использовалась. К 1980-м годам речь уже идет о неверных мужьях, и головоломка становится темой исследования одной из научных лабораторий IBM.[146] Джон Аллен Паулос дал в книге Once upon a Number («Жило-было число»), опубликованной в 1998 году, версию, так похожую на ту, что используется Microsoft, что, возможно, корпорация использовала именно этот источник.[147]

Я подозреваю, что типичный читатель этой книги прочитал головоломку, подумал о ней немного, не придя ни к какому выводу, и заглянул в ответ: «Вот это да! Какая замечательная головоломка!» Потом, возможно, загадал ее двум-трем друзьям, которые также не сумели ее решить, но согласились, что у нее потрясающее решение, когда узнали о нем. Популярность логической головоломки никак не зависит от того, может кто-то ее решить или нет.

Это становится проблемой только если кто-то пытается использовать данную головоломку для отбора кандидатов на работу. Хотя в причудливой «рекурсивной» логике, используемой для решения этой задачи, можно найти определенные параллели с программированием, эту головоломку очень трудно решить людям, которые понимают поведение реальных людей (а это полезное качество даже для программиста). Когда они не могут ее решить, это обычно происходит из-за того, что они приходят к верному заключению, что если уж ничего не происходит сразу после заявления королевы, то с течение времени драматизм ситуации будет только ослабевать. Обычно это вполне разумный вывод, если речь идет не о решении логических головоломок.

Злобный демон поймал много гномов (их точное количество неизвестно)…

Какие выводы может сделать в этой ситуации безупречно логичный гном? Наверное, никаких. Скорее всего типичный гном видит других гномов с зелеными или красными камнями. Он все еще ничего не знает о том, какого цвета камень у него на лбу.

Но представьте, что есть гном, который видит только красные или только зеленые камни на лбу у других гномов. Поскольку демон сообщил всем гномам, что среди них есть хотя бы один такой, у которого красный камень на лбу, гном, который видит только зеленые камни, может прийти к выводу, что он и есть единственный гном с красным камнем. И наоборот: гном, который видит только красные камни, может заключить, что он — единственный гном с зеленым камнем на лбу.

Теперь подумайте о гипотетическом гноме, который видит вокруг только гномов с зелеными камнями. Он должен понять, что у него на лбу — красный камень. Все, что ему нужно сделать — просто шагнуть вперед на следующей перекличке после объявления демона. Он может быть уверен в том, что его безупречно логичные товарищи останутся в строю. Это и будет правильным ответом, который потребовал демон.

Вы можете спросить: а почему другие гномы останутся в строю? Потому ли, что они знают, что у них зеленые камни? Нет. Каждый из этих гномов видит один красный камень (на лбу у того гнома, который собирается выйти из строя) и много зеленых камней (у всех остальных). Это не позволяет никому из них дедуцировать цвет их собственных камней. Они знают, что должен быть хотя бы один камень каждого цвета, и они видят по крайней мере один камень каждого из цветов. Их собственный камень может быть любого цвета.

Эти гномы остаются в строю, потому что им неизвестен цвет их собственного камня. Помните, если кто-то сделает неверный шаг, все гномы погибнут. Логика подсказывает, что единственное безопасное решение — оставаться в строю, если только гном не уверен в том, что у него на лбу красный камень.

Это еще не решение проблемы. Это только один из возможных сценариев, который проще всего анализировать. Это не значит, что именно это реальная ситуация: нам только сообщили, что гномов много, но неизвестно, сколько точно и красные у них на лбу камни или зеленые.

Если описанный выше сценарий не будет реализован во время первого построения (а скорее всего он не будет реализован), все гномы могут прийти к выводу, что есть по крайней мере два камня каждого из двух цветов. Это могло быть очевидно с самого начала. (если бы все гномы видели много камней разного цвета), но если бы был гном, который бы видел только один камень данного цвета, он мог бы во время второго построения прийти к выводу, что он — вторая персона с камнем этого цвета. Он и второй гном с камнем этого цвета (который рассуждает идентичным образом) сделают шаг вперед во время второго построения… Эта цепочка рассуждений и метарассуждений (рассуждений о рассуждениях) будет продолжаться, пока количество построений после объявления демона не совпадет с реальным количеством гномов с камнями более редкого цвета. На этом построении все безупречно логичные гномы с камнем этого цвета сделают шаг вперед, и (если демон держит свои обещания) все гномы обретут свободу.

Любому студенту, который изучает программирование, известно имя Алонзо Черча. В 1930-х годах Черч сформулировал так называемый тезис Черча — Тьюринга — краеугольный камень в исследованиях искусственного интеллекта (суть тезиса в том, что компьютер можно запрограммировать делать все то, что могут делать люди). Черч также один из немногих людей, которых можно обоснованно считать авторами логических головоломок мирового класса. Примерно в то же время, когда он сформулировал свой знаменитый тезис, он придумал головоломку о трех садовниках, у которых были пятна грязи на лбу. Их видит другой человек и замечает, что по крайней мере у одного из них грязь на лбу. Каждому из садовников нужно дедуцировать, грязный у него лоб или чистый.

Эта головоломка послужила вдохновением для целого жанра задач о людях, которые должны дедуцировать, какого цвета у них на голове шляпа или печать на лбу. В последние годы Раймонд Смаллиан предложил много вариаций хороших задач на эту тему. Тем или иным способом практически все эти головоломки решаются на основе предположений о поведении безупречно логичных существ, которые делают выводы на основе того, что их коллеги, также безупречно логичные существа, не делают определенного вывода в течение какого-то определенного срока.

Головоломка о «деревне неверных мужей», наверное, самый вычурный вариант. Задача о демоне и гномах отличается от нее тем, что вам, когда вы рассуждаете, нужно поставить себя на место одного из участников этой гипотетической ситуации и продумывать свою стратегию поведения. Я нигде не нашел упоминаний именно об этой версии задачи, автор которой, видимо, не понаслышке знал об опасностях работы в большой организации с плоской организационной структурой.

Четырем туристам нужно ночью переправиться через реку по подвесному мосту…

Никто не знает, почему у туристов имена музыкантов из группы U2.

Поскольку фонарик только один и без него никак не обойтись — единственный способ переправляться через мост такой: двое людей переходят на другую сторону, а потом одному из них нужно вернуться назад с фонариком. Чистый результат такого цикла — один человек переправляется через пропасть.

Когда два человека идут по мосту вместе, то общая скорость будет скоростью более медлительного из них. Если Адам переправляется вместе с Боно, то ему придется идти так же медленно, и этой паре потребуется для переправы через мост десять минут.

Вам может показаться, что для того, чтобы все четверо переправились, им понадобится четыре перехода туда и обратно. К счастью, это неверно.

Последний переход не требует возврата и позволяет переправиться через пропасть сразу двоим туристам. Таким образом, вам понадобятся два с половиной перехода туда и обратно, и в последний переход переправятся сразу двое.

Наиболее привлекательной идеей, пожалуй, представится такая: поручить Адаму, который переправляется через мост всего за одну минуту, сопровождать своих более медлительных друзей.

Во время первого перехода на другой берег пойдет Адам с самым медлительным из туристов Боно (ему нужно десять минут). Эта пара переправится за десять минут.

Потом Адам переправится обратно с фонариком (на это уйдет всего одна минута).

Теперь Адам пойдет через мост вместе со вторым медлительным спутником Эджем (которому требуется пять минут) и снова вернется назад (еще одна минута).

Наконец, через мост пойдут Адам и Лари (две минуты). Полное время: 10+ 1 + 5 + 1 + 2 = 19 минут. Это на две минуты дольше, чем требуется.

Если бы такая ситуация сложилась в реальной жизни, то большинство людей, вероятно, пришли бы к заключению, что она безнадежна. Нужно тянуть соломинки или проститься с Боно. Наверное, единственное обстоятельство, которое заставит вас продолжать поиски решения, — то, что у логических головоломок решение обязано существовать.

Попробуйте старый трюк и перечислите все ваши предположения. Самое основное из них — кто-то должен возвращаться, чтобы вернуть фонарик на тот берег, где его ждут спутники, верно?

Трудно понять, как можно разрешить эту проблему. В условии задачи четко говорится, что никто не может перейти мост без фонарика. (Если вы попробуете как-то «перехитрить» это условие, например перебросить фонарик через пропасть или использовать бечевку для перетаскивания фонарика через пропасть, интервьюер скажет вам, что это недопустимо.)

Мы также предположили, что два человека переправляются через пропасть, а назад возвращается один из них с фонариком. Может быть, стоит попробовать другие варианты?

Нет смысла совершать такие «переходы», которые никому не позволяют переправиться через пропасть. Кроме того, нам сказали, что трех людей (или больше) мост не выдержит. Это оставляет всего две возможности: по мосту идет один человек или два человека. Если вы и подумали о «полном цикле в обратную сторону», то есть это такой вариант, когда вы поручаете кому-то переправить обратно человека, уже перешедшего через пропасть, — в этом нет смысла. Мы вернулись к тому, с чего начинали.

Почему бы не послать на ту сторону вместе двух самых медлительных туристов? В любом случае Боно один израсходует большую часть из разрешенных семнадцати минут, почему бы не убить сразу двух зайцев, послав его вместе с также медлительным Эджем — в этом случае хотя бы Эдж не будет никого тормозить.

Эта идея — ключ к решению. Есть шанс, что, читая эти строки, вы воскликнете: «Я уже думал об этом! Ничего не получается!»

Дело в том, что это одна из тех хороших идей, которую легко испортить. Большинство людей подумает о том, чтобы начать с того, чтобы отправить Боно и Эджа вместе на другую сторону. И к чему это приведет?

У вас на другой стороне окажутся двое невыносимо медлительных людей с единственным фонариком. Это значит, что кому-то из них, вероятно Эджу, придется отправиться обратно (он пойдет медленно), чтобы переправить фонарик. На это уйдет пятнадцать минут, а еще трое людей, включая Эджа, не переправились через мост, и уже одно это не позволит этой троице переправиться за семнадцать минут.

Некоторые люди на этом и остановятся. Легко предположить, что подобное фиаско демонстрирует ложность ключевой идеи. Другие люди задумываются о том, не оставить ли этот переход пять/десять минут на самый конец. Последний переход особый, поскольку после него никому не нужно переправлять обратно фонарик.

Эта идея оказывается ничуть не лучше. Каким образом Эдж и Боно могут оказаться перед мостом с фонариком, когда двое других туристов уже переправились на другую сторону? Только если один из них (скорее всего Эдж?) уже побывал на той стороне и вернулся обратно с фонариком, но в этом случае на дорогу туда и обратно уже было потрачено десять минут, или фонарик вернул назад кто-то из их более проворных товарищей, но тогда он тоже ждет на этой стороне, чтобы переправиться. Это приводит к тем же проблемам, которые мы уже рассматривали раньше.

Вот тут многие люди и сдаются. Они исследовали два экстремальных варианта (медлительная пара переправляется первой или последней) и убедились, что они неэффективны.

Но эти крайние варианты — не единственная возможность. Медлительная пара может переправляться в середине. Вот что позволяет найти решение.

Цикл номер один: самая быстрая пара, Адам и Лари, переправляется через пропасть, потратив на это две минуты. Один из них (допустим, Адам — не важно, кто именно) немедленно возвращается обратно (на это уходит одна минута). На все это уйдет три минуты.

Цикл номер два: самая медленная пара, Эдж и Боно, переходят через мост, потратив десять минут. Как только они переправятся на другую сторону, они уже больше по мосту не путешествуют. Они передают фонарик более проворному товарищу, который уже там их поджидает (это Лари, предполагая, что Адам уже вернулся на исходный берег во время первого цикла). Лари приносит фонарик туда же (на это уйдет две минуты). Всего потрачено пятнадцать минут.

Наконец, последний третий цикл — переход только в одну сторону. Быстрая пара сейчас на исходной стороне. Они переходят пропасть во второй и последний раз (у них уходит на это две минуты). Всего потрачено семнадцать минут.

Корни этой головоломки можно обнаружить еще в раннем средневековье. Аббат Алкуин (735-804)[148] записал собрание головоломок, в которое вошла и ранняя версия хорошо знакомой многим головоломки о человеке, которому нужно было переправить через реку волка, козу и капусту. Козу нельзя оставлять вместе с волком, а козу — без присмотра вместе с капустой. За прошедшие с того времени двенадцать столетий было создано много вариаций на тему этой головоломки. Река иногда заменяется мостом, который вот-вот обвалится, или на блок, веревку и ведро, с помощью которых люди могут сбежать из башни. Ограничениями могут быть вес, время, запрет на то, чтобы оставлять женщин без присмотра, или уже упоминавшиеся выше отношения между хищником и его добычей. Головоломка о каннибалах и миссионерах, которым нужно переправиться через реку в двухместной лодке (в любой момент, когда каннибалов окажется больше, чем миссионеров, они съедят миссионеров), сыграла свою роль в первых исследованиях искусственного интеллекта. Уже первые программы ИИ смогли найти решение этой задачи.

Задача, используемая Microsoft, — одна из самых сложных в этом жанре. Она активно рассылалась по электронной почте в сопровождении своей «городской легенды». В этой легенде утверждалось, что «…один парень решил эту задачу, написав программу на языке С, правда, ему потребовалось на это 17 минут. Группа из 50 сотрудников компании Motorola так и не смогла ее решить… Обратите внимание: Microsoft требует, чтобы вы решили эту задачу не дольше, чем за 5 минут».[149] (На самом деле это не так.)

Перед вами две двери. Одна приведет вас в комнату, где вы пройдете интервью, а другая — на улицу…

Поскольку вы не знаете, скажет вам консультант правду или нет, бессмысленно задавать ему вопрос: «Это верная дверь?» или «Вы в этой компании работаете?» Вы получите ответ, который может оказаться и правдивым, и лживым. Используя свой единственный вопрос, вы не сумеет определить, правда это была или ложь. Вместо этого вам нужно придумать такой вопрос, что будет неважно, сказал консультант вам правду или солгал. Для этого нужно использовать двойное отрицание. К примеру, указать на дверь (не важно на какую) и сказать: «Если бы я спросил вас, этим ли путем я попаду на интервью, вы бы ответили да?»

Основная идея заключается в том, что законченный лжец солжет и насчет своего ответа на прямой вопрос о том, какая дверь приведет вас на интервью (который вы на самом деле ему не задавали!). Итак, законченный лжец скажет прямо противоположное тому, что бы он сказал, если бы ему задали прямой вопрос, то есть ложному ответу. Эти две лжи нейтрализуют одна другую, и получится, что лжец ответит вам «да» только в том случае, если вы указали на верную дверь. Что касается правдивого консультанта, то он тоже ответит «да» только если вы указали на верную дверь, потому что он, конечно, ответил бы так же и на прямой вопрос. Вы не узнаете, кто вам ответил — лжец или правдивый консультант, зато вы найдете нужную дверь.

Есть ряд альтернативных решений. Одно из них такое: «Если бы я спросил консультанта из другой фирмы, приведет ли эта дверь меня на интервью, он бы ответил утвердительно?» Все такие решения требуют, чтобы консультанты пожелали разобраться в подобных запутанных вопросах и дали на них ответ в том духе, в каком он ожидается. Но такие вопросы рискуют привлечь внимание лжеца к тому, что происходит нечто странное. Лучше, если лжец будет «безупречным лжецом», какие существуют только в логических головоломках. Если лжец будет действовать не так бездумно, как ожидается, и в первую очередь станет заботиться о том, чтобы обмануть, он может использовать тройное, а не двойное отрицание, чтобы сбить вас с толку.

Это можно обойти. Покажите на дверь и скажите: «Простите, я хотел бы пройти интервью в вашей компании — я попаду на него через эту дверь?»

Трюк с двойным отрицанием даст такой же результат, но данный вопрос звучит гораздо более естественно и позволяет лжецу солгать, не вдаваясь в сложный анализ. Это потому, что вам самому удается солгать (но только в том случае, если вы говорите с лжецом!), так как вы вовсе не хотите проходить интервью в фирме лжеца. Поэтому, если вы показываете на выход (который на самом деле как раз и может привести вас в фирму, где работает лжец, расположенную где-то на другом конце города), лжец солжет и скажет: «Нет, это не та дверь». А если вы покажете на дверь, которая должна на самом деле привести вас на интервью в нужной вам фирме, то есть на дверь, которая не приведет вас на интервью в конкурирующую фирму, на которую работает лжец, ему все равно придется солгать и сказать вам, что она туда приведет.

Эта версия «только с одним вопросом» старой загадки о лжеце и правдивом, похоже, появилась в 1950-е годы.[150] В той версии речь обычно шла о двух племенах правдивых и лживых, которые живут на далеком острове. Но была еще и несправедливо приписываемая Microsoft задача, которая активно распространялась в Интернете, предлагавшая новый поворот.[151] Вы оказались на перекрестке. Одна дорога ведет в Microsoft, другая — в фирму Utopia. Вы хотите попасть в Utopia. Вас встречает человек, у которого на голове коробка с Microsoft Windows. Вы не знаете, кто он — лжец, правдивый человек или Билл Гейтс. Вам разрешается задать ему только один вопрос. Какой это будет вопрос?

Когда эта задача появилась в тематической конференции rec.puzzles в Интернете, она вызвала целый шквал шутливых ответов, многие из которых были неистово «антимайкрософтовскими». Если вы считаете, что Билл Гейтс — сложная личность, о степени правдивости которой у нас нет никаких предположений, эта головоломка не имеет решения. Это все равно что заявить: «Вы оказались на острове Манхэттен, некоторые жители которого говорят правду, а некоторые — нет». Если же вы считаете, что Гейтс, что бы о нем ни говорили во время федерального расследования, не станет вас обманывать, когда вы попросите его указать дорогу, то он «считается» в этой головоломке честным и правдивым человеком, и тогда подходит прежнее решение.

Большинство решений, появившихся на rec.puzzles, были куда более творческими. Одно из них предлагало спросить того человека: «Куда я хочу сегодня пойти?» и сделать противоположное тому, что он ответит (на тех основаниях, «что они даже этого еще не поняли в Microsoft»[152]). В другом решении предлагалось спросить у этого парня: «Какой путь мне посоветует выбрать человек из другого племени?» и затем стукнуть его. «Если этот человек — правдивый или лжец, вы узнаете от него, какая дорога ведет в Utopia, а если нет — вам удастся отвесить бесплатную оплеуху Биллу Гейтсу».[153]

Почему банки для пива сужаются вверху и внизу?

Если ваша догадка — это делает банки более прочными, то это, в общем, верно. Сужения вверху и внизу связаны с общей конструкцией банки. Это «архитектурный вопрос»: жестяные банки, как и подвесные мосты, работают как единое целое. Это часто означает, что нелегко дать конкретное объяснение, почему какая-то деталь выглядит именно так.

Если говорить об истории сужений — изначально они не были предназначены для того, чтобы банки были крепче. Банки и так были достаточно прочны, чтобы держать в них пиво. А что еще требуется от пивной банки? Сужения были элементом конструкции, который позволял уменьшить расход металла. Это может показаться пустяковой экономией, если только вы не задумаетесь о том, сколько банок выпускается и перерабатывается каждый год.

Было время, когда пиво и газированные безалкогольные напитки выпускали в тяжелых стальных банках, которые были в сечении почти прямоугольными. Сталь должна была быть достаточно толстой, чтобы выдержать давление газированных напитков. Эти банки изготавливались из трех частей, это значит, что закругленные верх и низ прикреплялись при помощи опрессовки к цилиндрической середине.

Когда компаниям, изготавливающим эти банки, пришлось больше заботиться о снижении затрат и охране окружающей среды, они перешли на более тонкие алюминиевые банки. Тонкий алюминий менее прочен. Подобно яичной скорлупе, сегодняшние банки делаются настолько тонкими, насколько это возможно, чтобы надежно сохранять их содержимое. Это требует применения «архитектурных трюков», в которых не было необходимости при использовании стальных банок.

Самая толстая и прочная часть банки — это ее верх, который крепится при помощи обжима. Он должен выдерживать усилие при открывании банки. Поскольку металл верхней крышки банки толще, производитель заинтересован в том, чтобы минимизировать диаметр этой крышки, поэтому диаметр верха немного меньше, чем диаметр середины, и, чтобы их можно было соединить, банка должна сужаться вверху (нельзя уменьшить диаметр всей банки, потому что в нее тогда поместится меньше пива). Но раз уж вы сузили верх, вам придется сделать то же самое и с донышком, чтобы банки можно было ставить друг на друга.

Есть уже одна причина, по которой банка внизу сужается. Донышко и средняя часть банки прессуются из одного листа тонкого алюминия, что позволяет избежать дополнительной операции — крепления донышка к банке. Это проще сделать, если в нижней части банка идет на конус, чем если бы требовался изгиб под прямым углом. Это сужение также делает банку чуть более устойчивой к вмятинам на концах.

Похожий вопрос для интервью: «Почему дно банки для кока-колы вогнуто внутрь?» (У пивных банок такое же вогнутое донышко.) Ответ таков: металл на донышке настолько тонкий, что, если бы донышко было плоским, оно бы легко деформировалось. Вогнутый металл прочнее, чем плоский, точно так же, как выпуклая яичная скорлупа делает его более прочным по сравнению с яйцами, у которых была бы кубическая скорлупа. Прочность не зависит от того, вогнутое донышко или выпуклое, но, если бы донышки были выпуклыми, банки нельзя было бы ставить друг на друга.

Сколько времени понадобится для того, чтобы передвинуть гору Фудзи?

Похоже, что этот вопрос был придуман в консалтинговой фирме Booz, Allen and Hamilton. Есть два возможных подхода к решению. Если вы решите передвинуть всю гору целиком — таким же способом, как европейские монархи заставляли своих инженеров перевозить в свои столицы египетские обелиски, я желаю вам удачи. В противном случае вы должны применить метод приблизительных вычислений Ферми. Для начала вы будете считать передвижение горы на новое место обычными земляными работами. Вам нужно оценить объем горы Фудзи «в самосвалах».

Отправной точкой для вычислений, вероятно, должен стать знаменитый силуэт горы Фудзи. Большинство американцев представляет его себе как полый конус, основание которого примерно в пять раз больше, чем высота. Большинство людей гораздо хуже может оценить высоту этой горы. Фудзи не может сравниться по этому параметру с самыми высокими горами (высота Эвереста около 29 тыс. футов, или 8848 метров). Но очевидно, что ее высота несколько тысяч футов. Давайте остановимся на удобном круглом числе 10 тыс. футов (это хорошая догадка, потому что на самом деле вершина горы Фудзи находится на высоте 12 387 над уровнем моря). Это значит, что высота нашего конуса 10 тыс. футов, а диаметр основания — 50 тыс. футов.

Если бы гора Фудзи была похожа не на конус, а на цилиндрическую жестянку, ее объем был бы равен произведению площади основания на высоту. Основание — это круг диаметром 50 тыс. футов. Квадрат со стороной 50 тыс. футов имел бы площадь 50 000 х 50 000 футов. Это 2,5 миллиарда квадратных футов. Но площадь круга, вписанного в подобный квадрат, будет меньше (если точно, то она составит Пи/4 от площади квадрата, или 79 процентов), поэтому давайте оценим ее как 2 миллиарда квадратных футов. Умножьте это число на высоту 10 тыс. футов и вы получите 20 триллионов кубических футов — это будет объем цилиндра, в который можно вписать гору Фудзи.

Но гора Фудзи больше похожа на конус. Если вы помните, что объем конуса — это одна треть от объема цилиндра с таким же основанием и высотой, это делает вам честь. Но даже если вы этого не помните, очевидно, что объем конуса должен быть меньше, чем объем эквивалентного цилиндра. Поскольку мы так любим круглые цифры, давайте сократим 20 триллионов кубических футов до 10 и будем считать, что объем конуса-горы Фудзи — 10 триллионов кубических футов вулканических пород.

Сколько это самосвалов? Самосвал может перевезти объем скальных пород объемом 10 на 10 на 10 футов. Это 1000 кубических футов. Таким образом, для перевозки горы Фудзи потребуется нагруст зить 10 миллиардов самосвалов.

Формулировка вопроса оставляет неопределенными многие параметры. Мы не знаем, куда мы передвигаем гору Фудзи. Попробуйте спросить об этом интервьюера. Мы также не знаем, какую долю объема горы составляет почва, которую легко погрузить экскаватором, а какую — твердые скальные породы, которые придется взрывать динамитом.

Даже в лучшем случае, чтобы нагрузить и перевезти один самосвал, потребуется полный рабочий день одного работника. Если считать, что один груз самосвала эквивалентен одному рабочему дню, то для того, чтобы передвинуть гору Фудзи, понадобится 10 миллиардов рабочих дней.

Длительность проекта будет зависеть от того, сколько людей станут выполнять эту работу. В абсолютно невероятном случае, если всю эту работу будет выполнять только один человек (естественно, таких людей придется после смерти заменять, подобно смотрителям маяков, на протяжении многих тысячелетий), для завершения работы понадобится 10 миллиардов дней, или примерно 30 миллионов лет. (Гора Фудзи, вероятно, столько времени и не существовала и вряд ли просуществует в своем нынешнем виде так долго. Она по естественным причинам исчезнет еще до того, как один человек сумеет ее передвинуть.)

Если будет реализован не менее невероятный вариант и удастся привлечь к этой работе все 6 миллиардов людей, населяющих земной шар (а также снабдить их необходимым оборудованием и сделать так, чтобы они не мешали друг другу), гору можно будет передвинуть за пару дней.

Представьте теперь, что правительство Японии решило передвинуть гору Фудзи и привлекло для решения этой задачи достаточно солидные ресурсы. Десять тысяч человек — примерно столько людей работает в больших корпорациях — это будет хорошая оценка. Им потребуется для решения задачи 10 миллиардов /10 000 дней. Это миллион дней, или примерно 3000 лет.

В коридоре три выключателя…

Это еще одна задача, которая кажется не имеющей решения. Если вы выключите все выключатели, то свет не будет гореть (и ваш поход в комнату вам ничего не скажет). Если же вы включите один из выключателей, вероятность того, что вы выбрали нужный, —один к трем. Если повезет, то свет будет гореть, и вы найдете нужный выключатель, но в двух из трех случаев свет гореть не будет, и у вас не будет возможности определить, какой из двух выключенных выключателей включает свет в комнате. Если вы включите два из трех выключателей или все три, то столкнетесь со сходными проблемами.

Если по-другому это сформулировать: для идентификации одного объекта из трех нужны два бита информации. Ваш единственный визит в комнату дает вам только один бит информации.

Если бы это были выключатели, которые не просто включают или выключают свет, но регулируют его интенсивность, задачу было бы легко решить. Вы бы один из них включили на полную мощность, второй выключили бы, а третий включили бы на 50 процентов. Тогда состояние лампочки подсказало бы вам, какой из выключателей ее контролирует.

Это, конечно, было бы решением, но головоломка была бы неинтересной, если бы в ее условии упоминался такой важный факт. Тем не менее это «решение» привлекает внимание к важному обстоятельству: если бы существовал способ установить один из выключателей в «промежуточное положение», а не просто в положение «включено» или «выключено», это позволило бы решить задачу.

Вот решение: пронумеруйте выключатели 1, 2 и 3. Затем включите выключатели 1 и 2 и выключите выключатель номер 3. Подождите примерно десять минут. Затем выключите выключатель номер 1, включите выключатель номер 2 и немедленно отправляйтесь в комнату.

Если свет там горит, значит, его включает выключатель номер 2. Если свет не горит, но лампочка теплая, его контролирует выключатель номер 1. Если свет не горит и лампочка холодная, его контролирует выключатель 3.

Вы играете в игру только с одним другим игроком…

Стратегии подобных, игр обычно достаточно сложные: если они задают вам такой вопрос во время интервью для отбора кандидатов на работу, это значит, что стратегия должна быть простой. Интервьюер не стал бы спрашивать вас об оптимальной стратегии игры в шахматы.

Право первого хода обычно дает преимущество. Когда вы играете в крестики-нолики, вам выгодно поставить первый крестик в центральную клетку. Вам нужно задать себе вопрос: «Есть ли такой уникальный первый ход, который может дать мне стратегическое преимущество?»

В данном случае нет центральной клетки — есть бесконечное множество мест, куда вы можете положить свою первую монету. Предположим, вы решили положить ее в северо-западный угол стола на том основании, что это особая, если уже не уникальная позиция. Даст ли это вам стратегическое преимущество?

Трудно сказать. Очевидно, что в этой игре придется сделать много ходов (понадобится много монет, чтобы закрыть ими весь стол так тесно, чтобы нельзя было больше положить на него ни одной монеты, которая бы не касалось монет, уже находящихся на столе). Возможно, игрок, делающий, первый ход, может получить преимущество, которое он сможет сохранить в течение всей игры, а может быть, и нет.

Не похоже, что занятие северо-западного угла стола даст вам уникальное стратегическое преимущество. Это не игра в «Монополию», где Променад дает вам более высокий доход, чем любая другая собственность. В нашем случае один угол ничем не лучше, чем любой другой. В действительности, если бы занятие угла давало бы какое-то преимущество, ваш противник ответил бы вам тем же, положив свою первую монетку в один из оставшихся незанятым углов. Если углы так важны, то первые четыре хода должны быть сделаны именно в углы, но тогда каждый из вас будет контролировать по два угла и никто не получит преимущества. И что тогда? Снова ваш ход, можно ли говорить о каких-то существенных изменениях?

Какой бы вы ни сделали первый ход, похоже, что ваш оппонент сможет его эффективно дублировать. Все, что ему (или ей) нужно сделать, это положить свою монетку в позицию, зеркально симметричную по отношению к вашему предыдущему ходу. Если вы сделали ход в северо-западный угол, оппонент займет юго-восточный угол и т.д.

Стоп! Есть только одно исключение — ход, который ваш оппонент не сможет дублировать. Этот ход — положить вашу первую монетку точно в центр стола. Хотя в этой игре и нет «центральной клетки», есть уникальная позиция в центре стола — как только вы положили туда монету, никто другой ее уже не сможет занять.

Это еще не значит, что ход в центр стола — это хороший ход, но это уникальный первый ход, единственный ход в этой игре, когда игрок имеет возможность сделать его так, чтобы второй игрок не смог этот ход копировать.

Запомните эту мысль…

Что бы вы ни делали, другой игрок может класть свои монетки почти где угодно в начальной стадии игры. Поэтому, если у вас есть хорошая стратегия, которая также должна быть и простой стратегией, она должна быть основана на не требующих особенных раздумий парирующих ходах, которые позволят вам легко нейтрализовать любой ход противника.

Теперь обобщите все, о чем шла речь выше. Поскольку вы ходите первым, вам нужно сделать первый ход, положив свою монету прямо в центр стола. После этого вы копируете «зеркально» предыдущий ход вашего оппонента. Вы просто должны мысленно соединить прямым отрезком его монетку и центр стола, потом продолжить эту линию и положить вашу монетку на нее с противоположной стороны от центра на точно таком же расстоянии, как это сделал ваш оппонент.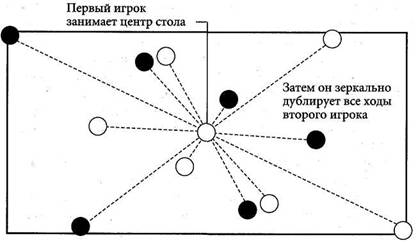

Вы всегда сможете так поступать, так как вы просто дублируете последний ход вашего оппонента (если стол симметричный). В конце концов именно вашему оппоненту не удастся положить еще одну монету на стол так, чтобы он не прикасалась ни к одной из тех, которые уже лежат на столе.

Британский эксперт по головоломкам Генри И. Дьюдени вызвал при помощи этой игры ажиотаж в своем клубе в Лондоне (там они выкладывали на стол сигары[154]). Игра описана в опубликованной в 1917 году книге Дьюдени Amusements in Mathematics («Математические развлечения»). Версия Дьюдени с сигарами была особенно хитрой. Его уловка, которая всегда приносила ему выигрыш, была такой: он ставил сигару в самый центр стола вертикально. Следующие сигары можно было также ставить на стол вертикально или класть их на стол — это было безразлично, поскольку Дьюдени всегда мог отвечать противнику симметричным ходом. Американский соперник Дьюдени Сэм Ллойд использовал его идею, творчески ее развив: он использовал в игре куриные яйца. Чтобы яйцо могло стоять, нужно сделать небольшую вмятину на тупом конце яйца.[155]

Пять пиратов на острове должны разделить между собой сотню золотых монет…

Насколько нам известно, у пиратов равные права на монеты. Простейший план — поделить монеты поровну на пять частей. Тогда каждый получит по двадцать монет. Что плохого в таком решении?

В общем ничего, за исключением того, что вас могут убить. Вы предложите такое решение, а другие четыре пирата могут подумать, что двадцать монет — это хорошее решение, но двадцать пять монет — еще лучше. Именно столько они и получат, если проголосуют против вашего плана и убьют вас. Потом они снова начнут делить ту же сотню монет, но пиратов теперь будет только четверо.

Вы можете до посинения спорить, утверждая, что поделить добычу поровну — это самый честный план, но в условии головоломки ничего не говорится о том, что пираты — люди честные. Честность — это обычно не самое нужное пиратам качество. Причем отвергнуто будет не только первое предложение поделить все поровну: то же случится и со следующими подобными предложениями. Ведь лучше делить добычу на троих, чем на четверых? А на двоих лучше, чем на троих? Вам понятно, к чему это все приведет?

Эта загадка напоминает телевизионное шоу «Последний герой». В этом шоу его участники голосуют за то, кого из соперников выгнать с острова, надеясь, что именно они останутся его последним обитателем и выиграют денежный приз. Участники этого шоу обычно стремятся к победе, формируя кратковременные коалиции. Сходный подход применяется и здесь. Поскольку вы рискуете своей жизнью, а не просто потерей возможности стать на пятнадцать минут «звездой экрана», вы хотите быть стопроцентно уверены, что ваш план раздела добычи будет принят.

Эта головоломка — еще одно упражнение в рекурсивных рассуждениях. Чтобы найти решение, нужно понять, что ситуацию с n пиратов можно анализировать на основе ситуации с n — 1 пиратов и т.д., пока вы не доберетесь до «базовой ситуации», решение в которой будет абсолютно ясным.

Базовая ситуация — это один выживший пират. Очевидно, что единственный пират предложит отдать ему все монеты. Ход сделан!

А что если пиратов двое? Старшему из них придется предложить, как делить добычу. В условии головоломки говорится, что предложение принимается, если «по крайней мере половина пиратов» за него проголосует. Это значит, что достаточно одного голоса старшего пирата, чтобы предложение было принято. Следовательно, если пиратов всего двое, то старшему из них бояться нечего, и он может не беспокоиться о том, что думает его товарищ. Будучи жадным негодяем, старший пират предложит отдать все сто монет ему. Результаты голосования будут такими: один голос «за» и один «против» — это значит, что предложение будет принято.

Может показаться, что старший пират всегда получит то, чего он хочет. Не совсем так. Представьте, что он решил воспользоваться тем же трюком, если пиратов трое. Давайте пронумеруем пиратов, начиная с самого младшего: №1, №2, №3. План раздела добычи должен предложить номер 3. Если он предложит такой план: «Все достается мне, а вы, ребята, ничего не получите», то следующий пират в этой последовательности (№2) точно проголосует против подобного предложения. Пират №2 знает, что он сам получит все, если останутся только два пирата после того, как №3 будет убит. Решающим оказывается голос пирата №1. Он ничего не получает, если проголосует за план пирата №3 , но также ничего не получит, если проголосует против, если останутся только два пирата. У него нет никаких причин, чтобы предпочесть один вариант другому.

Итак, если №3 умен, как это предполагается в головоломках, он попытается получить поддержку пирата №1. Нужно также учесть, что пират №3 жадный, и он готов отдать другому пирату только необходимый минимум. Логичным предложением со стороны пирата №3 будет дать №1 одну золотую монету, №2 — ничего, а ему самому — оставшиеся девяносто девять монет! Поскольку №1 также рассуждаете логично, но поймет, что и эти жалкие гроши лучше, чем ничего, а ведь он ничего не получит, если пират №3 будет убит. Пират №1 проголосует за план раздела добычи (как и №3, конечно), и это предложение будет принято двумя голосами против одного несмотря на все проклятия накачавшегося с горя ромом пирата №2.

Теперь рассмотрим ситуацию с четырьмя пиратами. Четыре — это опять четное число. Это значит, что самому старшему пирату достаточно всего одного голоса, кроме его собственного, чтобы его предложение прошло. Ему нужно ответить на вопрос: «Какой из голосов остальных трех пиратов окажется самым дешевым?»

Вернемся к ситуации с тремя пиратами. Пират №2 не получает в ней ничего, поэтому если пират №4 предложит ему хотя бы что-то, то для пирата №2 будет логично проголосовать «за».

И получив голос пирата №2, пират №4 может совсем не беспокоиться о том, что думают №1 и №3. План пирата №4 будет таким: ни одной монеты для №1, одна монета для №2, ни одной монеты для №3 и девяносто девять монет для него самого.

Теперь модель нам ясна. В каждом случае самый старший пират должен «купить» ровно столько голосов, сколько ему необходимо, и как можно дешевле. Все остальные деньги достанутся ему самому.

Теперь применим эту модель к ситуации с пятью пиратами, о которой речь и идет в задаче. Вы пират №5. Вам нужно три голоса: ваш собственный и еще два. Таким образом, вам нужно что-то дать двум пиратам, которые больше всего проиграют, если пиратов останется только четверо. Это пираты №1 и №3. Оба не получат ничего, если вас убьют и останется всего четыре пирата. Обоих можно убедить проголосовать за ваш план, если он им что-нибудь сулит. Ваше предложение: ничего не давать пирату №4, дать одну монету №3, ничего не дать №2 и дать одну монету №1. Оставшиеся девяносто восемь монет вы оставите себе.

Это одно из тех абсолютно не соответствующих здравому смыслу решений, которые убеждают многих людей в абсурдности логических головоломок. Если бы пираты формировали коалиции на основе дружеских отношений (что и происходит в телешоу «Последний герой»), все эти рассуждения оказались бы бессмысленными. Но даже если не принимать в расчет возможные дружеские коалиции, решение все равно выглядит сомнительным. Вы можете поверить, что пираты (или наркоторговцы, мафиози, какие-нибудь другие бесчестные эгоисты) спокойно проголосуют за схему, которая вам дает девяносто девять монет, а они получают или одну монетку, или вообще ничего? Да остальные четверо сначала вас застрелят, а уже потом станут заниматься дедукцией.

Эту головоломку использует компания Fog Creek Software из Нью-Йорка. По этому поводу в одной из интернет-конференций появилось сообщение: «Готов поклясться, что генеральный директор Fog Creek загребает 98 процентов прибылей этой компании. Реальная причина, по которой в ней задают этот вопрос, — желание найти смиренных овечек, готовых с этим мириться, если получат какое-нибудь математическое объяснение».[156]

В одной из школ есть такой ритуал в последний день занятий…

Первая вещь, которую необходимо понять, — эта головоломка просто обязана быть проще, чем она кажется на первый взгляд. Ваши интервьюер слишком занят, чтобы сидеть и ждать, пока вы пройдете все сто шагов. Должен быть какой-то трюк, который позволит упростить решение, и ответ должен быть относительно простым. Или все 100 шкафчиков должны остаться открытыми, или ни один из них, или должна отыскаться какая-то закономерность, которая позволит легко решить, сколько будет открытых шкафчиков.

Ваш нетерпеливый интервьюер некоторое время будет сидеть спокойно, пока вы начертите таблицу с номерами с первого по десятый. Сделайте это и делайте отметку в клетке, относящейся к данному шкафчику, если положение его дверцы изменилось. Например, в первом цикле все 100 шкафчиков будут открыты. И вы поставите в таблице соответствующие отметки.

Во втором цикле вы поставите отметки в клетках с четными номерами 2,4,6,8 и 10. Продолжите это до десятого цикла (если бы вы продолжили это делать до 20, 30, 40 и т. д. — у вас получилась бы полная таблица). После десяти циклов ваша таблица будет выглядеть так:

И следующие циклы никак не повлияют на первые десять шкафчиков — ведь во время одиннадцатого цикла будет меняться положение дверец только шкафчиков номер 11, 22, 33… Таким образом, составленная вами таблица для первых десяти ящиков окончательная. Поскольку в начале шкафчики были закрыты, то все шкафчики, положение дверец которых изменилось нечетное количество раз, останутся открытыми, а если положение менялось четное количество раз, шкафчики будет закрытыми.

Это означает, что после 100 циклов шкафчики 1, 4 и 9 останутся открытыми, а все остальные закрытыми. 1,4 и 9 — это точные квадраты, то есть числа, умноженные сами на себя (1 = 1х1; 4 = 2х2; 9 = 3x3). Это очень привлекательная закономерность.

Вы понимаете, почему открытыми остались только те шкафчики, номера которых — это квадраты какого-то числа? Вы столько раз меняете положение дверцы шкафчика, сколько есть множителей в числе, соответствующем его номеру, а эти множители — парные. Например, двенадцать — это 1х12, или 2x6, или 3x4. Поскольку есть три способа разбиения этого числа на пары сомножителей, общее число сомножителей — шесть. Это значит, что положение дверцы этого шкафчика изменится шесть раз. Единственный способ, которым число может избежать четного количества сомножителей, — это такая ситуация, когда его можно представить как пару из двух идентичных сомножителей. Например, девять можно представить как 1 х 9 и также как 3x3. Это дает только три различных сомножителя (1, 3 и 9). Только те шкафчики, номер которых — это квадрат какого-то числа, будут открываться/закрываться нечетное количество раз, и только их дверцы останутся открытыми.

Такие числа в первой сотне это: 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100. Ответ на задачу: открытыми будут десять шкафчиков.

У вас есть два куска бикфордова шнура…

В более простой версии этой головоломки, которую также используют в интервью, спрашивают, как отмерить тридцать минут при помощи тех же бикфордовых шнуров. Поскольку она легче, с нее и начнем.

Возможностей немного: если вы подожжете оба шнура, вы не узнаете, сколько прошло времени, пока огонь не добежит до конца, а это будет шестьдесят минут. Никакого прока.

Обратите внимание на то, что вы можете найти середину длины каждого из шнуров без линейки, просто сложив их пополам. Но если вы подожжете любой шнур в его середине, вы также ничего не узнаете, потому что он горит неравномерно, следовательно, огонь доберется до его концов не одновременно. Хотя сумма времени, за которое сгорают обе половины, — шестьдесят минут, вам это никак не поможет. Если взять предельный случай, то может оказаться, что правая половина шнура горит сверхбыстро — всего одну минуту, а левая, напротив, сверхмедленно — целых пятьдесят девять минут. Это не поможет вам узнать, когда прошло тридцать или сорок пять минут.

Исчерпывает ли это все возможности? Нет. Умная идея — положить два шнура крест-накрест, в форме буквы X. Положите их так, чтобы они пересекались в середине длины каждого из шнуров, прикасаясь друг к другу. Тогда, если вы подожжете один из концов буквы X, огонь доберется до середины, а дальше пойдет сразу в трех направлениях. Все, чего мы добьемся таким способом — второй шнур начнет гореть с середины своей длины (но мы уже знаем, что это нам ничего не дает), и мы не будем знать, сколько времени пройдет (то есть за какое время огонь доберется до пересечения). Что в лоб, что по лбу!

Исчерпаны ли все возможности? Нет: вы можете поджечь бикфордов шнур сразу с обоих концов.

Скорость, с которой движется огонь, сама по себе для нас не важна, и огоньки, двигающиеся с двух концов шнура навстречу друг другу, совсем не обязательно встретятся в середине, но где-то они обязательно встретятся. Когда они встретятся, это будет означать, что каждый из них горел время, равное половине от шестидесяти минут, то есть тридцать минут.

Отлично! Это решение для более легкой версии задачи, которое также позволит нам решить и 45-минутную версию. Итак, поджигая один из шнуров с обоих концов, мы можем отмерить тридцать минут. Если бы нам удалось при помощи второго отрезка шнура отмерить еще пятнадцать минут, мы бы решили головоломку.

Мы уже знаем, что можем уменьшить вдвое время горения любого отрезка шнура, поджигая его одновременно с двух концов. Если бы у нас был отрезок, сгорающий за тридцать минут, мы могли бы поджечь его с обоих концов в тот самый момент, когда догорел бы первый шестидесятиминутный отрезок, подожженный с двух концов. Это как раз и дало бы нам недостающие пятнадцать минут, и мы бы получили искомые сорок пять минут.

У нас нет отрезка шнура, который сгорает за тридцать минут, но мы можем его получить, если подожжем второй кусок шнура только с одного конца, пока мы отмеряем тридцать минут при помощи первого отрезка.

Вот вся процедура: сначала мы одновременно поджигаем отрезок А с обоих концов и отрезок В только с одного конца. Эти отрезки не должны соприкасаться. Пройдет тридцать минут, пока не сгорит шнур А (два огонька, движущиеся навстречу друг другу, встретятся). Когда это произойдет, то есть пройдет ровно тридцать минут, у отрезка В остается длины на тридцать минут горения. Мы должны немедленно поджечь второй конец все еще горящего отрезка В. Два огонька встретятся через пятнадцать минут, а всего пройдет сорок пять минут.

Вы находитесь в лодке точно в центре абсолютно круглого озера…

Именно так, и вы понимаете, в чем проблема: очевидный план — со всей скоростью грести к берегу по прямой к той точке, которая дальше всего от той точки, где гоблин находится сейчас. Это даст вам существенное дистанционное преимущество: вам ведь нужно проплыть только расстояние, равное радиусу (r) круглого озера. А гоблину, который не может плавать, придется бежать по дуге вокруг озера дистанцию, равную половине длине окружности озера. Это расстояние Пиr. Гоблину, таким образом, придется преодолеть дистанцию в п раз большую, чем вам.

Число п чуть больше, чем три. Если бы гоблин двигался ровно в три раза быстрее, чем ваша лодка, вы бы его чуть-чуть опередили. Вот почему в головоломке говорится, что гоблин движется в четыре раза быстрее, чем лодка. Не важно, где вы попытаетесь выбраться на берег, — гоблин успеет туда раньше и схватит вас.

Как и во многих других случаях, при решении этой головоломки нужно сначала выяснить ряд важных неопределенностей. Что собой представляет гоблин — то ли он просто бездумный «магнит», скользящий вокруг озера к самой близкой к вам точке, то ли он разумное или даже умное существо? Поскольку вам сказали, что гоблин «безупречно логичен», очевидно, подразумевается последнее. Похоже, что вам придется перехитрить гоблина. Но это непросто. На озере негде спрятаться, а безупречно логичный гоблин может продумать ваши возможные стратегии, и это значит, что врасплох вам его не застать.

Для начала притворимся, что гоблин — это «бездумный магнит», который отслеживает каждое ваше движение и старается держаться к вам как можно ближе. Вот как вы можете попробовать его обхитрить: сделайте небольшой круг в середине озера. Это изрядно досадит гоблину — он попытается обежать вокруг все озеро (а ваша лодка проплывет всего несколько метров). Гоблин не сможет поспеть за вашей лодкой, потому что ему придется описать гораздо больший круг, чем пройдет ваша лодка. Это значит, что, описывая такие круги, вы сможете оказаться от гоблина на расстоянии больше радиуса, если измерить его по прямой, проходящей через центр озера.

Это подсказывает решение. Спросите себя: «Каков радиус самого большого круга с центром в середине озера, по которому я могу двигаться так, чтобы гоблин успевал за мной?»

Это должен быть такой круг, который позволил бы вам преодолевать расстояние, составляющее четверть того, что преодолевает гоблин. Это круг с радиусом r/4.

Начинайте двигаться по этому кругу по часовой стрелке, и гоблину придется со всей скоростью бежать также по часовой стрелке, чтобы оставаться в самой близкой к вам точке на берегу озера. Если же вы поплывете против часовой стрелки, гоблину придется сделать то же самое. А теперь вот в чем главная хитрость. Если вы станете двигаться по кругу с радиусом чуть меньшим, чем r/4, гоблин уже не сможет поспевать за вами. Он начнет постепенно отставать.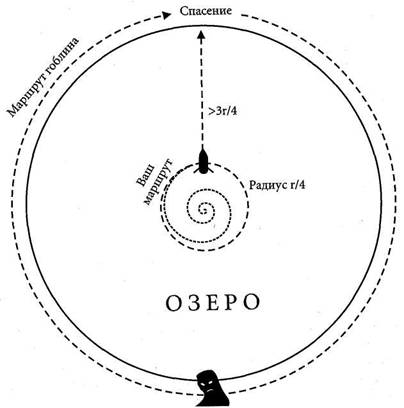

Это значит, что вы сможете оказаться от гоблина на расстоянии 11/4 радиуса. Один из способов добиться этого — начать движение по спирали от центра озера, приближаясь к окружности радиусом r/4, но все-таки оставаясь внутри нее. Пока вы будете внутри «этого зачарованного круга», гоблин не сможет успевать за вами. Вы можете плыть таким образом, пока гоблин не отстанет от вас на полные 180 градусов. Тогда ваша лодка будет на противоположной от гоблина стороне озера (по отношению к центру озера) и на расстоянии по прямой от гоблина в 5/8 диаметра озера (вы на одной прямой, проходящей через центр озера с гоблином, и гоблин на расстоянии радиуса от центра, а вы на расстоянии от центра почти в 1/4 радиуса, или в 1/8 диаметра). Такие геометрические соотношения дадут вам возможность спастись. Вы немедленно перестаете кружиться и по прямой устремляетесь к самой дальней от гоблина точке на берегу озера. Вам нужно покрыть дистанцию чуть больше, чем 3/4 радиуса, а гоблину — расстояние Пиr. То есть ему придется преодолеть расстояние в 4Пи/3 раз большее, чем вам, и, поскольку гоблин двигается в четыре раза быстрее, чем вы, ему для этого потребуется время, которое можно вычислить, умножив необходимое вам время на 7Пи/3. Значение числа Пи больше, чем три (если точно, в 1,047… раза), и это значит, что если вы все выполните по плану, то успеете высадиться на берег и убежать от гоблина до того, как он сумеет вас поймать.

Действительно ли это решение головоломки? Что, если гоблин умен и уже знает о подобном плане? Ему необязательно подобно преданному псу кружиться за вами вокруг озера, особенно если он понимает, что вы затеваете.

Да, но даже если гоблин абсолютно точно знает, что вы планируете сделать, это ему не поможет. Вы можете взять мегафон и прокричать: «Эй, гоблин! Вот что я обязательно сделаю. Я буду крутиться вокруг озера по этому маленькому кругу с радиусом чуть меньше, чем одна четвертая часть радиуса озера. Ты сам можешь все подсчитать! Как только я окажусь в точке окружности на расстоянии в 180 градусов от тебя, я поплыву к берегу, и мы оба знаем, что я успею тебя обогнать. Теперь мы можем решить нашу проблему легким способом, трудным способом или глупым способом. Легкий способ — ты признаешь, что проиграл и спокойно даешь мне возможность доплыть до противоположного берега и убежать от тебя. Трудный способ — ты будешь гоняться за мной. Это потребует от нас обоих больших усилий, но результат все равно окажется точно таким же. Наконец, вот глупый способ. Если ты попытаешься применить „контрстратегию“, то есть бежать не на полной скорости, бежать в противоположную сторону, бегать туда-сюда или даже отбежать подальше от озера, все эти трюки только помогут мне быстрее оказаться от тебя на расстоянии в половину окружности (180 градусов), и я все равно убегу от тебя».

В разных компаниях применяют разные вариации этой головоломки. Иногда вы оказываетесь в середине круглого поля, огороженного колючей проволокой, вокруг которого бегает собака-убийца, стремящаяся до вас добраться. В еще одной версии это лиса, которая пытается поймать утку, плавающую в середине круглого озера (хотя трудно себе представить утку, хорошо знающую геометрию).

Всегда ли солнце всходит на востоке?

Ответом должно быть «нет». Некоторые люди начинают приводить космические примеры. Венера и Уран вращаются вокруг своей оси в направлении, противоположном направлению вращения Земли. Или если поместить в пространстве воображаемую невращающуюся платформу, то солнце вообще не будет всходить или заходить. Строгий интервьюер не примет подобные ответы и переформулирует вопрос так: «Всегда ли солнце всходит на востоке на Земле?» Ответ все равно должен быть «нет». На Северном полюсе вообще нет такого направления, как восток: любое направление укажет на юг. Во время шестимесячного полярного «дня» солнце и всходит, и заходит на юге. На Южном полюсе — обратная ситуация: там любое направление указывает на север.

У вас есть шесть спичек. Сложите их так, чтобы получились четыре равносторонних треугольника.

Подразумевается решение (а), сложить из спичек трехгранную пирамиду (тетраэдр). Почти всем трудно найти идею трехмерного, а не двухмерного решения.

Есть также два двухмерных решения, но по сравнению с тетраэдром они кажутся слишком прозаическими. Одно — это сложить «звезду Давида», сложив два пересекающихся треугольника, каждый из трех спичек. В концах звезды расположены шесть маленьких равносторонних треугольников (плюс два больших, и того получается восемь). Те, кто стремится к совершенству, могут, сдвинув одну из спичек, получить ровно четыре (маленьких) равносторонних треугольника.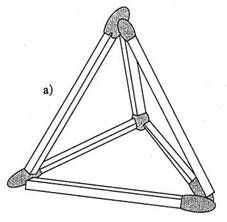

ГРАУЧО[*]: Послушай-ка. У меня есть для тебя классная работа, но сначала тебе придется ответить на пару важных вопросов. Вот… Кто имеет четыре пары штанов, живет в Филадельфии и никогда не льется как дождь, а только моросит?

ЧИКО: Классная загадка. Дам тебе три подсказки.

ГРАУЧО: Постой-ка… Имеет четыре пары штанов, живет в Филадельфии… Это мужчина или женщина?

ЧИКО: Нет, не думаю.

ГРАУЧО: Оно мертво?

ЧИКО: Кто?

ГРАУЧО: Я не знаю. Я сдаюсь! ЧИКО:

Я тоже сдаюсь!

— Граучо и Чико Маркс в комедии« Утиный суп» (1933 год, сценарий Берта Калмара, Харри Руби, Артура Шикмана и Ната Перрина).

Оглавление